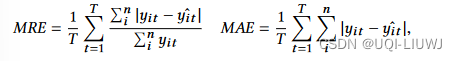-
论文笔记:Region Representation Learning via Mobility Flow
2017 CIKM
1 摘要和介绍
- 使用出租车出行数据学习区域向量表征
- 同时考虑时间动态和多跳位置转换
- ——>通过flow graph和spatial graph学习表征
- 出租车交通流可以作为区域相似度的一种
- A区域和B区域之间流量大
- ——>A和B的特征更相关
- ——>用一个/很相似的vector来表征他们
- 之前的文献中,使用一个转移矩阵来表示流量数据的mobility
- 每一个区域使用一个n维向量表征,其中的第j个元素表示从i到j/从j到i的流量
- ——>使用这样的转移矩阵也会有问题,那就是没有考虑时间动态
- 比如A区域到B区域是早上流量多,C区域到B区域是晚上流量多;但A和C区域在特征上可能是不同的
- 可以创建了一个tensor(加入了时间维度),而不是一个matrix来表征mobility
- ——>使用这样的转移矩阵也会有问题,那就是没有考虑时间动态
- 每一个区域使用一个n维向量表征,其中的第j个元素表示从i到j/从j到i的流量
- 但是这样会存在一定问题
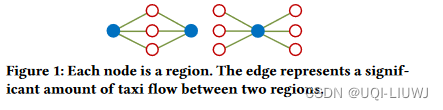
- 比如左图的两个蓝点之间并没有直接的流量 ,没法建模他们的相似性
- ——>解决方法是multi-hop的转换矩阵
- 创建了一个新的flow graph
- 每一个节点表示一定时间间隔内的一个区域
- 每一条边表示不同区域在不同时间间隔内的转移
- 与此同时,论文使用了另一个空间图(捕获区域间的空间邻接关系)
- 创建了一个新的flow graph
- A区域和B区域之间流量大
2 preliminary——generalized inference model
- 输入K个不重叠的区域
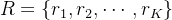 、部分区域的目标属性的观测值(第i个区域的是yi)、所有区域的辅助feature (第i个区域的是
、部分区域的目标属性的观测值(第i个区域的是yi)、所有区域的辅助feature (第i个区域的是 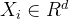 )
) - 目标是估计每个区域的目标属性(第i个区域的是yi)
- 为了预测各个区域的yi,使用如下的回归模型
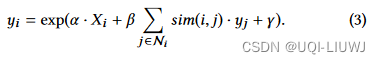
- 其中α、β和γ是回归模型的参数
- sim(i,j)表示区域i和区域j之间的相似度
- Ni是邻居节点集合
3 问题定义
3.1 输入数据
- 输入数据:
- mobility data
- 包括了n段旅途
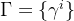
- 每段旅途的格式是
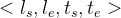 ,分别表示起始和结束位置的坐标和时间
,分别表示起始和结束位置的坐标和时间
- 包括了n段旅途
- 空间信息
- 城市中K个不重叠的位置组成,
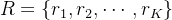
- 城市中K个不重叠的位置组成,
- mobility data
3.2 时间增强节点
- 在论文中涉及的一张异构图中,使用时间增强节点来区分区域
- 每个节点被记为
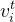 ,表示t时刻的区域i
,表示t时刻的区域i - ——>一共有KT个时间增强节点
- 每个节点被记为
- 给定了这些时间增强节点后,可以捕获两种关系
- 从不同区域之间的mobility flow中得到的关系——>图Gf
- 空间邻接关系——>图Gs
- 论文中提出的方法从两种图中同时学习空间表征
3.3 问题定义
- 给定flow graph Gf和spatial graph Gs,目标是学到每个时间增强节点
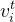 的表征
的表征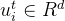
- 两个区域embedding之间的相似度用
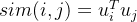 定义
定义
4 方法
4.1 flow graph
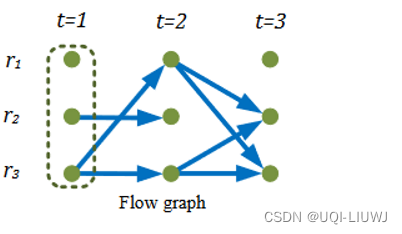
- 每一条边表示的时T时刻在位置A,T+1时刻在位置B
- 边权重就是流量大小
- 个人理解,图中t=1时刻的r2能够连接t=2时刻的r2,是因为这辆出租车载客从r2出发,兜了一圈又回来了(可能是乘客下了,又回到了扬招点)
但这个图会存在三个问题
- 无法描述“停留在某个点"这类情况
- ——>r2(t=1)到让r2(t=2)有连边,是环线的结果,并不是停留在原地的结果
- 数据很稀疏
- 有些区域在某些时刻可能没有交通流数据
- flow graph将所有时间加强点都视为独立的点。但是,不同时刻相同/相近点之间的关系无法刻画
4.2 spatial graph
- 节点集和flow graph的一样
- 不同时刻相同点之间有连边,数值为1
- 只有相邻时刻之间的点会有连边(t=1这一列的点和t=2这一列的点之间有边;t=1这一列的点和t=3这一列的点之间就没有边)
- 这种连边的边权重大小是
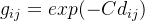 ,其中C是参数,dij表示i和j区域的距离
,其中C是参数,dij表示i和j区域的距离
- 这种连边的边权重大小是

4.3 异构图
将上面的两个图拼起来
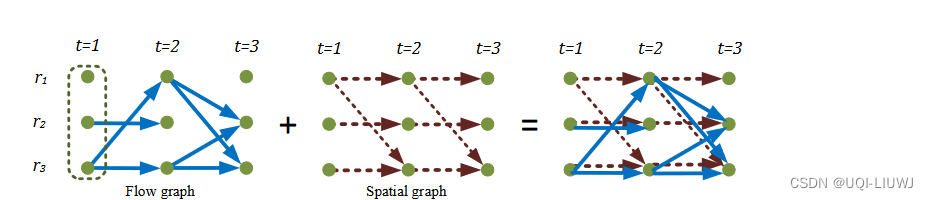
- 这样可以表示”停留在某地“这种情况了
- 同时由于节点是时间增强节点,所以时序关系以及多跳时序关系都是保留的
4.4 embedding的目标
4.4.1 单图上
- 几个定义
- 路径(path)
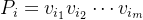
- 一条路径包含点
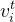 ——>
——>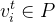
- 包含
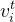 的路径集合
的路径集合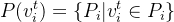
- 一个点
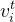 的上下文(context)——所有包含
的上下文(context)——所有包含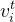 的路径上的点(除了
的路径上的点(除了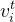 之外)
之外)
- 路径(path)
- 使用skip-gram模型学习embedding
- 理论值

- 在t时刻从点i出发,目标是点c的概率
- 实际值
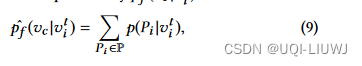
- P表示每一条从
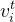 出发到vc的路径
出发到vc的路径 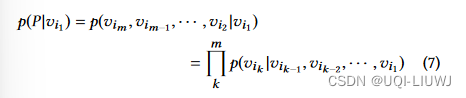
- 由于马尔可夫性质,7可以写成
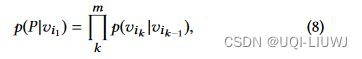
- P表示每一条从
- f是单图上对应边的权重
-
目标是理想值和理论值越近越好
-

-
D是衡量两个分布距离的(常见的有KL散度)
-
- 理论值
4.4.2 异构图
spatial 图类似
所以总的目标是
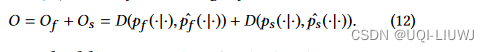
4.5 embedding学习的优化
4.4 存在的问题有:
- (5)式要计算所有对的话,需要
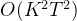 次操作(KT个点,两两成对)
次操作(KT个点,两两成对) - (9)式需要计算所有的路径(路径数量式节点数量的指数倍)
解决方法:负采样/随机游走
5 实验部分
5.1 实验配置
- 这篇paper提出的方法记作HDGE(heterogeneous dynamic graph embedding);如果是单个图的,就是
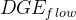 和
和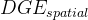
- metric是MRE和MAE
- 数据集有5个 :Demographics data + POI data + Taxi data + Crime data + House price data
- 作者首先使用KDD 2016的Crime Rate Inference with Big Data 模型作为RAW模型,进行特征选取(用哪些特征来预测另外一个效果更好)
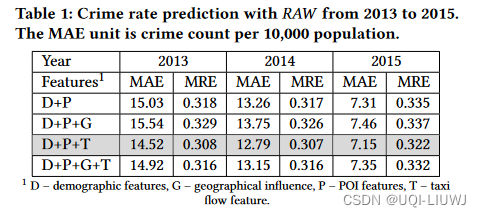
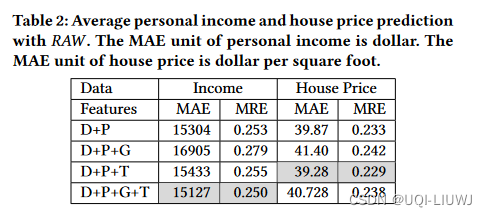
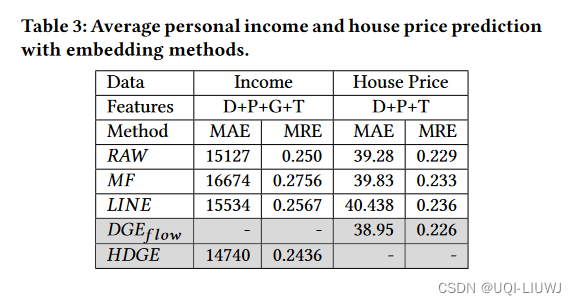
5.2 实验效果
- 根据上面的特征选取,crime rate prediction使用的是D+P+T的组合;Income prediction使用的是D+P+G+T;House Price prediction使用的是D+P+T
-
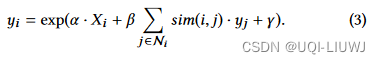 的similarity使用embedding之间的内积来计算
的similarity使用embedding之间的内积来计算
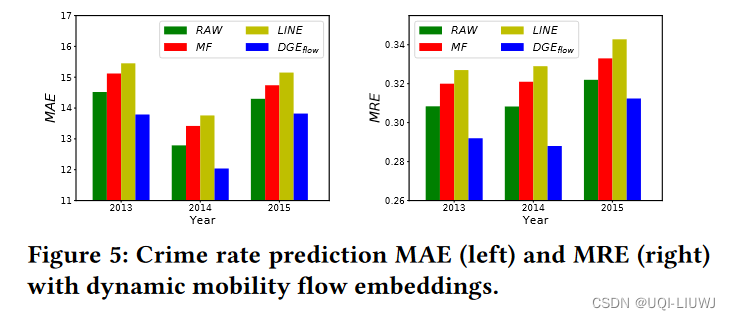
- 这里
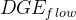 效果最好
效果最好
- ——>DGE使用多跳信息
- ——>DGE捕捉了时间转移信息
- LINE和MF只考虑了独立的一个一个embedding,空间转换信息并没有考虑,所以效果更差
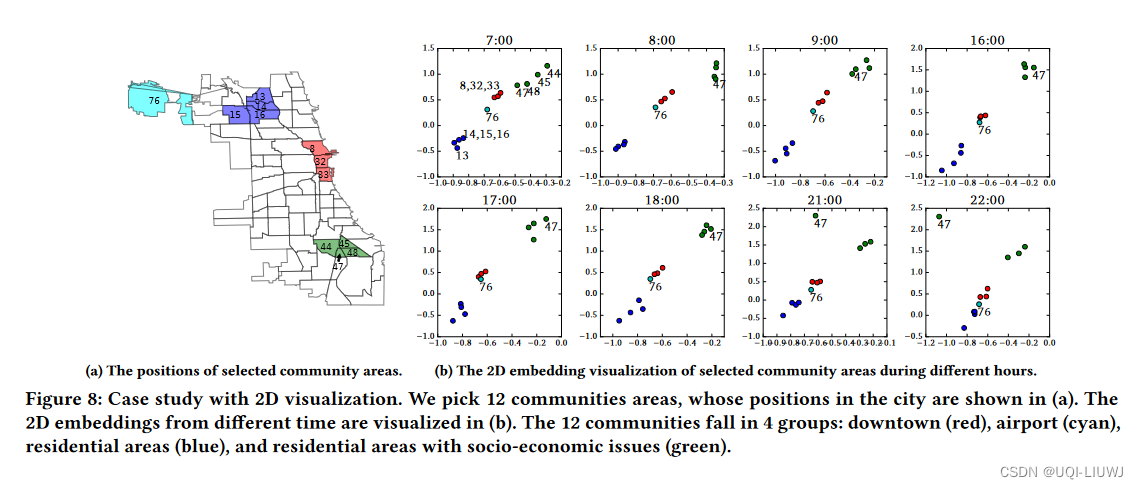
5.3 可视化结果
- 可以看到相邻区域的embedding很接近
- 不同时间同一区域的embedding差别也是有的
- 使用出租车出行数据学习区域向量表征
-
相关阅读:
Java底层HashMap的如何解释?
vue中用xlsx、xlsx-style、file-saver插件实现用表格原始数据打印excel文件
【C++】函数重载 ④ ( 函数指针定义的三种方式 | 直接定义函数指针 | 通过 函数类型 定义 函数指针 | 通过 函数指针类型 定义 函数指针 )
JVM之【字节码/Class文件/ClassFile 内容解析】
序列式容器——vector
2022年数维杯国际大学生数学建模挑战赛C题如何利用大脑结构特征和认知行为特征诊断阿尔茨海默病解题过程
uni-app:js时间与时间戳之间的转换
few shot目标检测survey paper笔记(迁移学习)
XXE漏洞详解:从基础到防御
Windows 安装 Docker Desktop 到其他盘、迁移虚拟硬盘映像文件、压缩虚拟硬盘映像占用空间
- 原文地址:https://blog.csdn.net/qq_40206371/article/details/127883848