数据的标准化处理——基于python

之前写过用R来进行标准化： 数据的标准化处理——基于R

归一化（normalization）

将数据缩放到[0,1]的（min—max Normalization）
$$X^{\ast }=\frac{X_i-X_{min}}{X_{max}-X_{min}}$$
通常将上面这种标准化称为归一化
缩放到[-1,1]的 Mean —Normalization
$$X^{\ast }=\frac{X_i-mean（X）}{X_{max}-X_{min}}$$

python实现

本次用到numpy和scikit-learn两个模块，请自行安装

import  numpy as np
from  sklearn  import  preprocessing
1
2

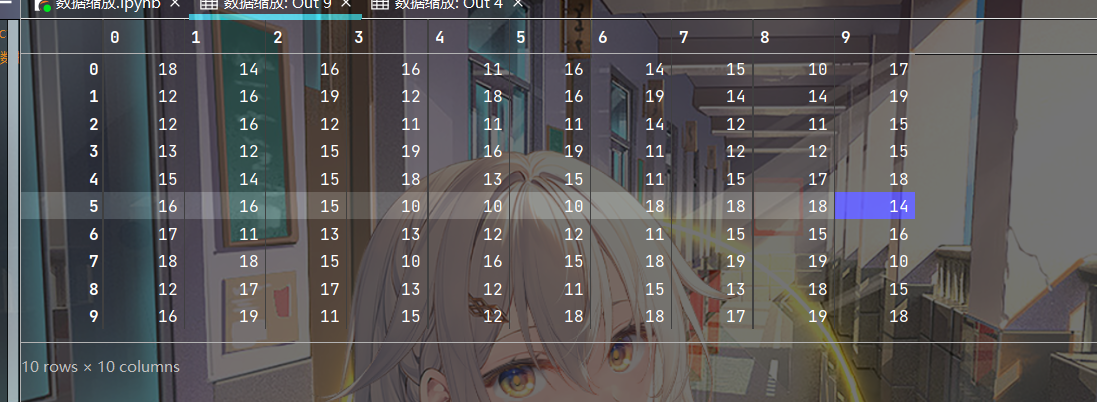
我们先用随机数生成一个十行十列的dataframe

feature=a=np.random.randint(low=10, high=20, size=(10,10))
feature
1
2

首先创建缩放器，注意代码里面的range就是我们缩放的范围

#创建缩放器
minmax_scale=preprocessing.MinMaxScaler(feature_range=(0,1))#这里的feature是固定的与数据名无关
scale_feature=minmax_scale.fit_transform(feature)#这里的future就是数据名
print(scale_feature)
1
2
3
4

输出结果：

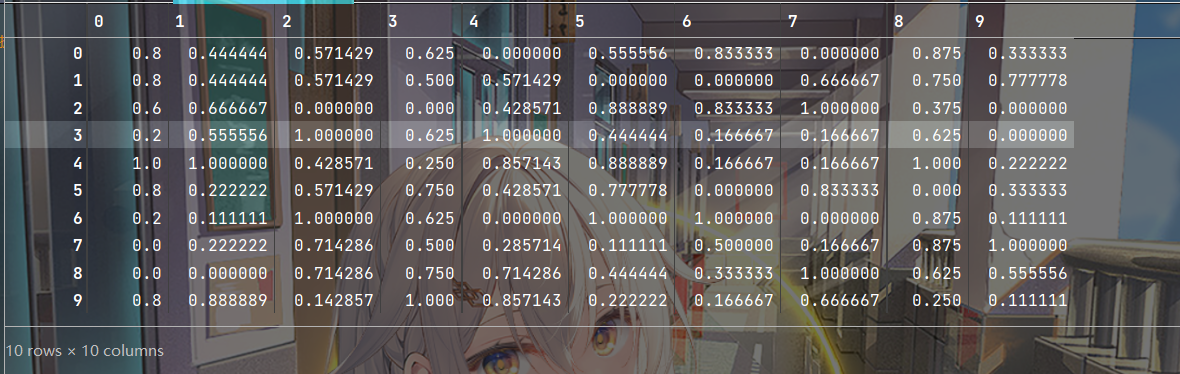
完整代码： 没有输出结果请加一个print

import  numpy as np
from  sklearn  import  preprocessing
#%% md

#%%
x=a=np.random.randint(low=10, high=20, size=(10,10))
# feature
#创建缩放器
minmax_scale=preprocessing.MinMaxScaler(feature_range=(0,1))
scale_feature=minmax_scale.fit_transform(x)
scale_feature
1
2
3
4
5
6
7
8
9
10
11

标准化

将数据变换为均值为0，标准差为1的分布，并非一定是标准正态的

$$X^{\ast }=\frac{X_i-\mu }{\sigma }$$

其中μ是均值，σ是标准差
数据的标准化并不会改变原有数据的分布，如果原有数据服从正态分布，则标准化后数据将服从标准正态分布

python实现

还是使用同样的库

import  numpy as np
from  sklearn  import  preprocessing
x=a=np.random.randint(low=10, high=20, size=(10,10))
1
2
3

#创建缩放器
minmax_scale=preprocessing.StandardScaler()
#转换特征
scale_feature=minmax_scale.fit_transform(x)
scale_feature
1
2
3
4
5

标准化后的数据

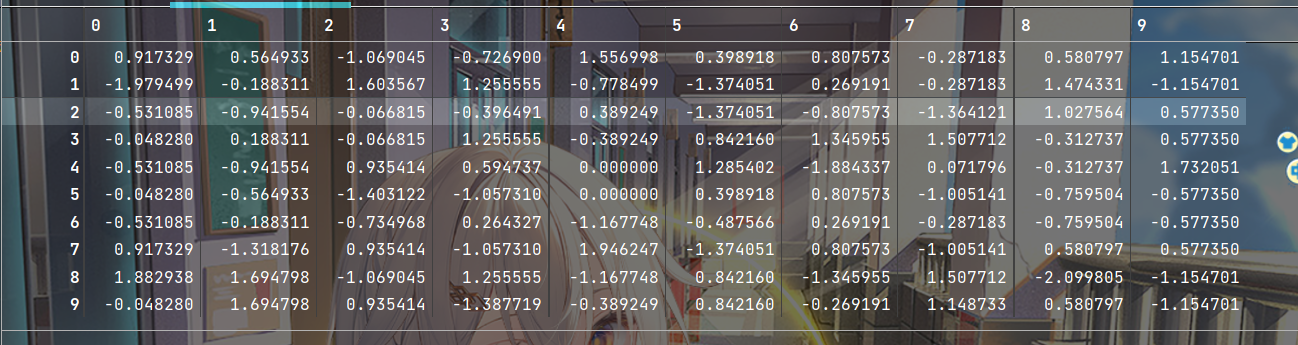
输出标准化后的均值和方差：

print(f"标准化后的均值为{round(scale_feature.mean(),2)},标准化后的均值为{round(scale_feature.std(),3)}")
1

标准化后的均值为-0.0,标准化后的均值为1.0

一般来说，第二个更常用一些