• 组成目标货币的最少张数

    1、题目

    arr 是货币数组，其中的值都是正数。再给定一个正数 aim。

    每个值都认为是一张货币，返回组成 aim 的最少张数。

    注意：因为是求张数，所以每张货币认为是相同或不同就不重要了。

    2、思路

    假设 arr = [3，1，3，5，1，1，1，5，3，2]

    则去重后的货币数组[3，1，5，2]

    每种货币的张数数组[3，4，2，1]

    尝试方式：讨论每个位置的货币用 i 张的情况，比如 0 位置的货币（3元）分别用 0 张、1 张、2 张和 3 张的情况。

    • 经典方法：货币不去重，讨论每张货币用和不用的情况
    //经典方法：货币不去重，讨论每张货币用和不用的情况
int minCoins(vector<int> &arr, int aim) {
    return process(arr, 0, aim);
}

//暴力递归
//index位置开始往后货币随意选择，组成rest的最少张数
int process(vector<int> &arr, int index, int rest) {
    if (rest < 0) {
        return INT_MAX;
    }

    if (index == arr.size()) {
        return rest == 0 ? 0 : INT_MAX;
    } else {
        //不使用index位置的货币
        int p1 = process(arr, index + 1, rest);
        //使用index位置的货币
        int p2 = process(arr, index + 1, rest - arr[index]);

        if (p2 != INT_MAX) {
            p2++; //加上index位置这张货币
        }
        return min(p1, p2);
    }
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 暴力递归改成动态规划
    //暴力递归修改成动态规划
//O(arr长度 * aim)
int dp1(vector<int> &arr, int aim) {
    if (aim == 0) return 0;

    int n = arr.size();
    int dp[n + 1][aim + 1];
    memset(dp, 0, sizeof(dp));

    dp[n][0] = 0;

    for (int j = 1; j <= aim; j++) {
        dp[n][j] = INT_MAX;
    }

    for (int index = n - 1; index >= 0; index--) {
        for (int rest = 0; rest <= aim; rest++) {
            int p1 = dp[index + 1][rest];
            int p2 = rest - arr[index] >= 0 ? dp[index + 1][rest - arr[index]] : INT_MAX;
            if (p2 != INT_MAX) {
                p2++;
            }
            dp[index][rest] = min(p1, p2);
        }
    }

    return dp[0][aim];
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28

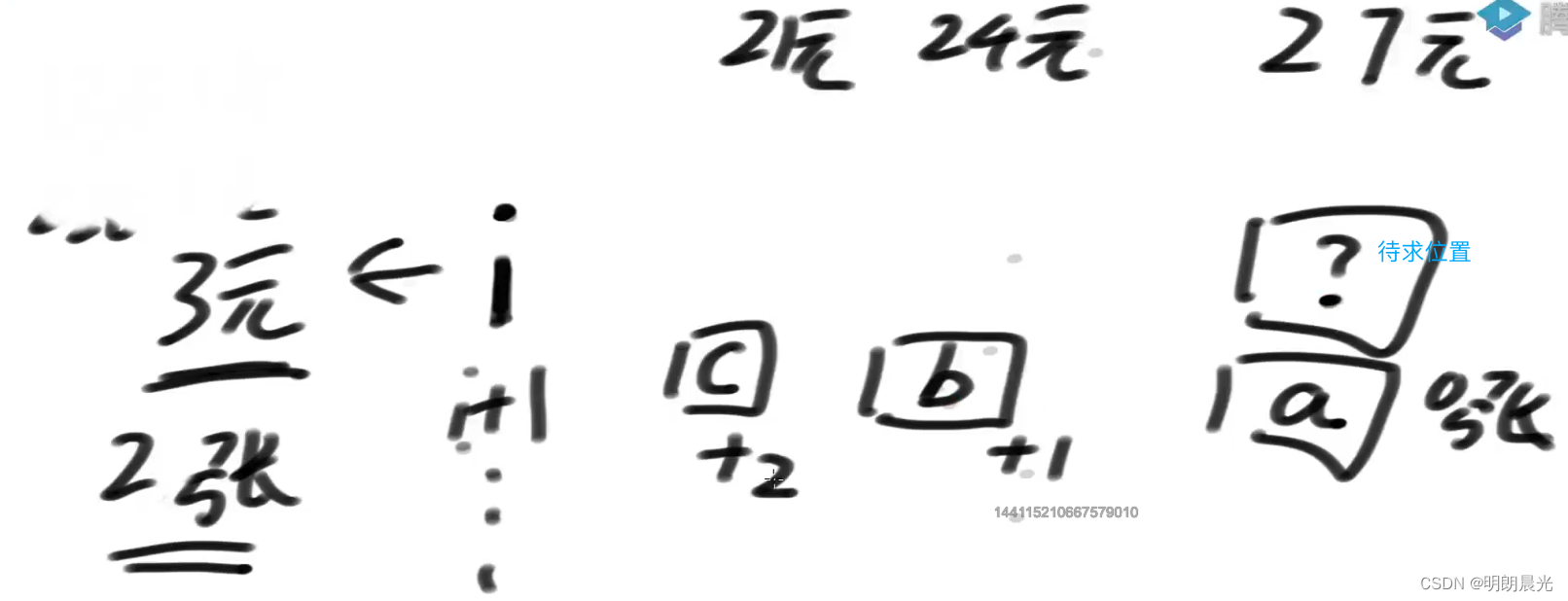
    假设当前来到了 i i i 位置，而该面值是3元，一共2张， i i i 及其往后的货币自由选择，如果要组成目标货币27元，求最小张数。

    分析该位置的求解需要依赖的值：

    1. 如果使用 0 张 i i i 位置的货币，则 i + 1 i + 1 i+1 及其后面的货币自由选择组成目标货币27元，如果需要 a a a 张；

    2. 而如果使用 1 张 i i i 位置的货币（3元）， i + 1 i+1 i+1 及其后面的货币自由选择组成27 - 3 = 24元，假设需要 b b b 张，再加上这一张3元，总共就是 b + 1 b + 1 b+1 张；

    3. 如果使用 2 张 i i i 位置的货币（3元）， i + 1 i + 1 i+1 及其后面的货币自由选择组成目标24 - 3 = 21元，假设需要 c 张，再加上这两张3元，总共就是 c + 2 c + 2 c+2 张；

    待求的位置的结果是 min{a + 0, b + 1, c + 2}，此过程涉及到了一个枚举行为。
    请添加图片描述
    代码实现如下：

    • 货币数组去重
    class Info {
public:
    vector<int> coins;
    vector<int> zhangs;

    Info(vector<int> &c, vector<int> &z) {
        coins = c;
        zhangs = z;
    }
};

Info *getInfo(vector<int> &arr) { //得到去重货币数组以及货币张数
    unordered_map<int, int> counts;
    for (int value : arr) {
        if (!counts.count(value)) {
            counts[value] = 1;
        } else {
            counts[value] += 1;
        }
    }

    int n = counts.size();
    vector<int> coins(n);
    vector<int> zhangs(n);

    int index = 0;
    for (auto entry : counts) {
        coins[index] = entry.first;
        zhangs[index++] = entry.second;
    }

    return new Info(coins, zhangs);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 货币数组去重后的动态规划
    //优化：去重版动态规划
//时间复杂度：O(arr长度) + O(货币种数 * aim * 每种货币的平均张数)
int dp2(vector<int> &arr, int aim) {
    if (aim == 0) return 0;

    Info *info = getInfo(arr); //得到info的时间复杂度O(arr长度)
    vector<int> coins = info->coins;
    vector<int> zhangs= info->zhangs;

    int n = coins.size();

    int dp[n + 1][aim + 1];

    memset(dp, 0, sizeof(dp));

    dp[n][0] = 0;

    for (int j = 1; j <= aim; j++) {
        dp[n][j] = INT_MAX;
    }
    //时间复杂度: O(货币种数 * aim * 每种货币的平均张数)
    for (int index = n - 1; index >= 0; index--) {
        for (int rest = 0; rest <= aim; rest++) {
            dp[index][rest] = dp[index + 1][rest];
            for (int zhang = 1; zhang * coins[index] <= aim && zhang <= zhangs[index]; zhang++) { //枚举
                if ((rest - zhang * coins[index] >= 0) && (dp[index + 1][rest - zhang * coins[index]] != INT_MAX)) {
                    dp[index][rest] = min(dp[index][rest], zhang + dp[index + 1][rest - zhang * coins[index]]);
                }
            }
        }
    }

    return dp[0][aim];
}

int compensate(int pre, int cur, int coin) {
    return (cur - pre) / coin;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38

    能否省掉这个枚举行为？

    看待求位置的前一个位置：同理上面的分析，X位置的结果是 min{b + 0, c + 1, d + 2}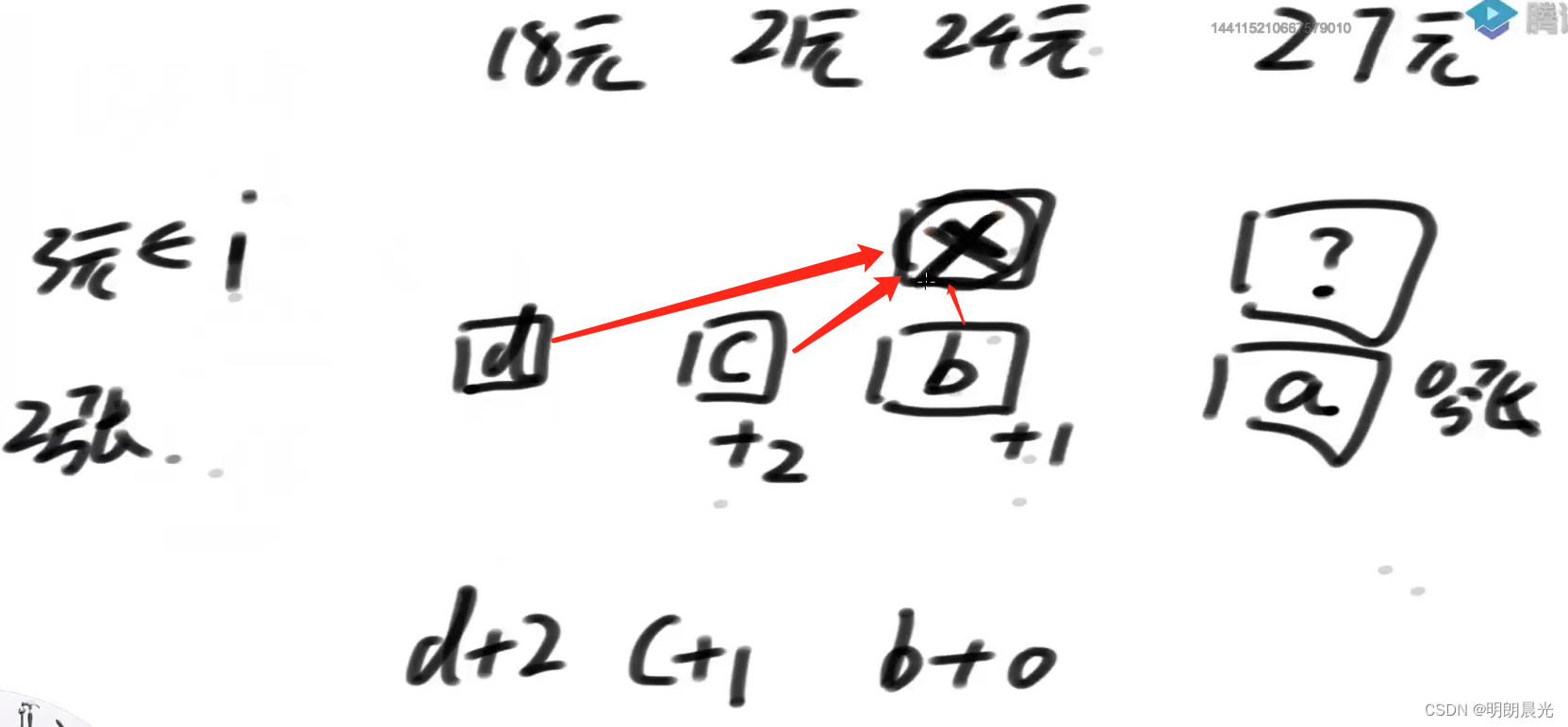

    请添加图片描述

    根据斜率优化，想省掉这个枚举行为，但是麻烦了。因为待求位置是 min{a + 0, b + 1, c + 2}，而x位置是 min{b + 0, c + 1, d + 2}，也就是说 x 位置依赖的窗口是 [d, c, b]，而待求位置依赖的窗口是 [c, b, a]，x并不知道d 滑出窗口后，最小值如何变化。因为 x 并不知道 d + 2, b + 1, a + 0 三个值谁胜出了，x 只记录一个最小值，所以x不知道在d滑出窗口后，最小值如何变化。这就比如果求的依赖的累加和麻烦。

    那么到底该怎么变呢？使用窗口内最大值和最小值的更新结构。

    抽象化：准备一个单调双端队列，存放最小值，即从队首到队尾，值从小到大。如果当前窗口内放着 x 元 a 张（队列内放的张数），而目前 y 元 b 张要入队，那么应该谁和谁比较呢？【a + (y - x) / 面值】 和 【b】 进行比较，就是说在比较的时候，必须是基于钱数相等的情况下，面值小的货币张数就要先补齐到货币值等于钱数。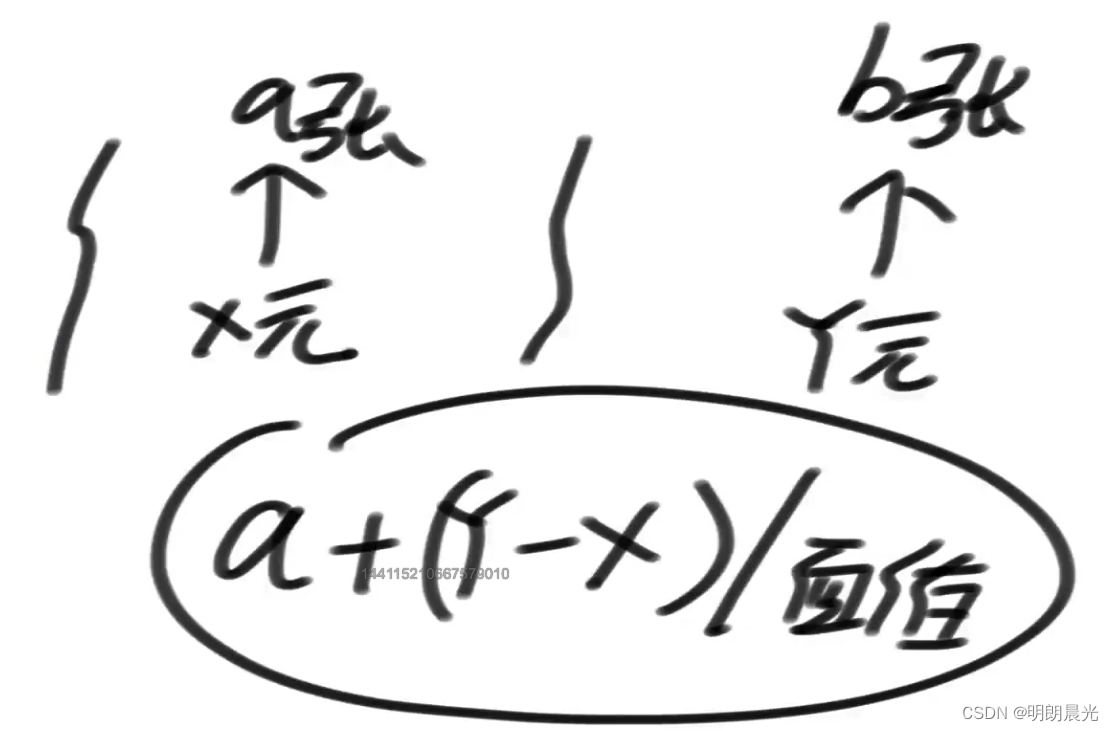

    请添加图片描述
    优化代码如下：

    • 优化版本：用到窗口内最小值的更新结构
    //时间复杂度: O(arr长度) + O(货币种数 * aim)
int dp3(vector<int> &arr, int aim) {
    if (aim == 0) return 0;

    Info *info = getInfo(arr);
    vector<int> c = info->coins;
    vector<int> z = info->zhangs;

    int n = c.size();

    //静态数组的局限性：占用的栈空间过大，导致无法申请声明数组
    vector<vector<int> > dp(n + 1, vector<int>(aim + 1, 0));

    dp[n][0] = 0;

    for (int j = 1; j <= aim; j++) {
        dp[n][j] = INT_MAX;
    }

    // 虽然是嵌套了很多循环，但是时间复杂度为O(货币种数 * aim)
	// 因为用了窗口内最小值的更新结构
    for (int i = n - 1; i >= 0; i--) {
        for (int mod = 0; mod < min(aim + 1, c[i]); mod++) {
            // 当前面值 X
			// mod  mod + x   mod + 2*x   mod + 3 * x
            deque<int> w;
            w.push_back(mod);
            dp[i][mod] = dp[i + 1][mod];

            for (int r = mod + c[i]; r <= aim; r += c[i]) {
                while (!w.empty() && (dp[i + 1][w.back()] == INT_MAX || dp[i + 1][w.back()] + compensate(w.back(), r, c[i]) >= dp[i + 1][r])) {
                    w.pop_back();
                }
                w.push_back(r);
                int overdue = r - c[i] * (z[i] + 1);
                if (w.front() == overdue) {
                    w.pop_front();
                }

                dp[i][r] = dp[i + 1][w.front()] + compensate(w.front(), r, c[i]);
            }
        }
    }

    return dp[0][aim];
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46

    优化的好处：如果不压缩数据（去重得到面值数组），那么填表的时间复杂度是 O ( n ∗ a i m ) O(n * aim) O(n∗aim)；但是压缩后，假设原数组长度为 n n n，去重得到的面值数组长度为 m m m，那么只需要一个 m ∗ a i m m * aim m∗aim 的表即可（时间复杂度 O ( m ∗ a i m ) O(m * aim) O(m∗aim)，且每个格子都是由窗口结构更新而来，时间复杂度为 O ( 1 ) O(1) O(1)，当货币出现大量重复的时候，就非常省时间。

    本题优化点：张数压缩；用窗口更新结构省掉枚举行为。

    3、完整代码

    C++ 版

    /*************************************************************************
	> File Name: 004.组成目标货币的最少张数.cpp
	> Author: Maureen 
	> Created Time: 三 11/16 15:12:39 2022
 ************************************************************************/

#include 
#include 
#include 
#include 
#include 
using namespace std;

//暴力递归
//index位置开始往后货币随意选择，组成rest的最少张数
int process(vector<int> &arr, int index, int rest) {
    if (rest < 0) {
        return INT_MAX;
    }

    if (index == arr.size()) {
        return rest == 0 ? 0 : INT_MAX;
    } else {
        //不使用index位置的货币
        int p1 = process(arr, index + 1, rest);
        //使用index位置的货币
        int p2 = process(arr, index + 1, rest - arr[index]);

        if (p2 != INT_MAX) {
            p2++; //加上index位置这张货币
        }
        return min(p1, p2);
    }
}

//方法1
//经典方法：货币不去重，讨论每张货币用和不用的情况
int minCoins(vector<int> &arr, int aim) {
    return process(arr, 0, aim);
}

//方法2：
//暴力递归修改成动态规划
//O(arr长度 * aim)
int dp1(vector<int> &arr, int aim) {
    if (aim == 0) return 0;

    int n = arr.size();
    int dp[n + 1][aim + 1];
    memset(dp, 0, sizeof(dp));

    dp[n][0] = 0;

    for (int j = 1; j <= aim; j++) {
        dp[n][j] = INT_MAX;
    }

    for (int index = n - 1; index >= 0; index--) {
        for (int rest = 0; rest <= aim; rest++) {
            int p1 = dp[index + 1][rest];
            int p2 = rest - arr[index] >= 0 ? dp[index + 1][rest - arr[index]] : INT_MAX;
            if (p2 != INT_MAX) {
                p2++;
            }
            dp[index][rest] = min(p1, p2);
        }
    }

    return dp[0][aim];
}


class Info {
public:
    vector<int> coins;
    vector<int> zhangs;

    Info(vector<int> &c, vector<int> &z) {
        coins = c;
        zhangs = z;
    }
};

Info *getInfo(vector<int> &arr) { //得到去重货币数组以及货币张数
    unordered_map<int, int> counts;
    for (int value : arr) {
        if (!counts.count(value)) {
            counts[value] = 1;
        } else {
            counts[value] += 1;
        }
    }

    int n = counts.size();
    vector<int> coins(n);
    vector<int> zhangs(n);

    int index = 0;
    for (auto entry : counts) {
        coins[index] = entry.first;
        zhangs[index++] = entry.second;
    }

    return new Info(coins, zhangs);
}

//方法3
//优化：去重版动态规划
//时间复杂度：O(arr长度) + O(货币种数 * aim * 每种货币的平均张数)
int dp2(vector<int> &arr, int aim) {
    if (aim == 0) return 0;

    Info *info = getInfo(arr); //得到info的时间复杂度O(arr长度)
    vector<int> coins = info->coins;
    vector<int> zhangs= info->zhangs;

    int n = coins.size();

    int dp[n + 1][aim + 1];

    memset(dp, 0, sizeof(dp));

    dp[n][0] = 0;

    for (int j = 1; j <= aim; j++) {
        dp[n][j] = INT_MAX;
    }
    //时间复杂度: O(货币种数 * aim * 每种货币的平均张数)
    for (int index = n - 1; index >= 0; index--) {
        for (int rest = 0; rest <= aim; rest++) {
            dp[index][rest] = dp[index + 1][rest];
            for (int zhang = 1; zhang * coins[index] <= aim && zhang <= zhangs[index]; zhang++) { //枚举
                if ((rest - zhang * coins[index] >= 0) && (dp[index + 1][rest - zhang * coins[index]] != INT_MAX)) {
                    dp[index][rest] = min(dp[index][rest], zhang + dp[index + 1][rest - zhang * coins[index]]);
                }
            }
        }
    }

    return dp[0][aim];
}

int compensate(int pre, int cur, int coin) {
    return (cur - pre) / coin;
}
//方法4
//优化需要用到窗口内最小值的更新结构
//时间复杂度: O(arr长度) + O(货币种数 * aim)
int dp3(vector<int> &arr, int aim) {
    if (aim == 0) return 0;

    Info *info = getInfo(arr);
    vector<int> c = info->coins;
    vector<int> z = info->zhangs;

    int n = c.size();

    //静态数组的局限性：占用的栈空间过大，导致无法申请声明数组
    vector<vector<int> > dp(n + 1, vector<int>(aim + 1, 0));

    dp[n][0] = 0;

    for (int j = 1; j <= aim; j++) {
        dp[n][j] = INT_MAX;
    }

    // 虽然是嵌套了很多循环，但是时间复杂度为O(货币种数 * aim)
	// 因为用了窗口内最小值的更新结构
    for (int i = n - 1; i >= 0; i--) {
        for (int mod = 0; mod < min(aim + 1, c[i]); mod++) {
            // 当前面值 X
			// mod  mod + x   mod + 2*x   mod + 3 * x
            deque<int> w;
            w.push_back(mod);
            dp[i][mod] = dp[i + 1][mod];

            for (int r = mod + c[i]; r <= aim; r += c[i]) {
                while (!w.empty() && (dp[i + 1][w.back()] == INT_MAX || dp[i + 1][w.back()] + compensate(w.back(), r, c[i]) >= dp[i + 1][r])) {
                    w.pop_back();
                }
                w.push_back(r);
                int overdue = r - c[i] * (z[i] + 1);
                if (w.front() == overdue) {
                    w.pop_front();
                }

                dp[i][r] = dp[i + 1][w.front()] + compensate(w.front(), r, c[i]);
            }
        }
    }

    return dp[0][aim];
}



//测试代码
vector<int> randomArray(int n, int maxValue) {
    vector<int> arr(n);
    for (int i = 0; i < n; i++) {
        arr[i] = (rand() % maxValue) + 1;
    }

    return arr;
}

void printArray(vector<int> &arr) {
    cout << "arr : ";
    for (int i = 0; i < arr.size(); i++) {
        cout << arr[i] << " ";
    }
    cout << endl;
}

int main() {
    int maxLen = 20;
    int maxValue = 30;
    int testTime = 300000 + 1;

    cout << "Function Test begin:" << endl;
    for (int i = 0; i < testTime; i++) {
        int n = rand() % maxLen;
        vector<int> arr = randomArray(n, maxValue);
        int aim = rand() % maxValue;

        int ans = minCoins(arr, aim);
        int ans1 = dp1(arr, aim);
        int ans2 = dp2(arr, aim);
        int ans3 = dp3(arr, aim);
        
        if (ans != ans1 || ans2 != ans3 || ans != ans2) {
            cout << "Oops!" << endl;
            printArray(arr);
            cout << "aim = " << aim << endl;
            cout << "ans = " << ans << endl;
            cout << "ans1 = " << ans1 << endl;
            cout << "ans2 = " << ans2 << endl;
            cout << "ans3 = " << ans3 << endl;
            break;
        }

        if (i % 10000 == 0) cout << i << " cases passed!" << endl;
    }
    cout << "Function Test ends!" << endl;
    cout << "===============" << endl;



    int aim = 0;
    vector<int> arr;
    long long start;
    long long end;
    int ans2;
    int ans3;
    cout << "Performance Test begin:" << endl;
    maxLen = 30000;
    maxValue = 20;
    aim = 60000;
    arr = randomArray(maxLen, maxValue);

    start = clock();
    ans2 = dp2(arr, aim);
    end = clock();
    cout << "ans2 = " << ans2 << ", dp2 cost " << (end - start) * 1000 / CLOCKS_PER_SEC << " ms" << endl;


    start = clock();
    ans3 = dp3(arr, aim);
    end = clock();
    cout << "ans3 = " << ans3 << ", dp3 cost " << (end - start) * 1000 / CLOCKS_PER_SEC << " ms" << endl;

    cout << "Performance Test ends!" << endl;
    cout << "===============" << endl;


    //以下测试的数据量只有dp3能通过，其它方法不能通过
    cout << "货币大量重复出现的情况下" << endl;
    cout << "大数据量测试滑动窗口方案开始:"<< endl;
    maxLen = 20000000;
    aim = 10000;
    maxValue = 10000;
    arr = randomArray(maxLen, maxValue);

    start = clock();
    ans3 = dp3(arr, aim);
    end = clock();
    cout << "dp3滑动窗口方案运行时间：" << (end - start) * 1000 / CLOCKS_PER_SEC  << " ms" << endl;
    cout << "大数据量测试滑动窗口方案结束" << endl;

    cout << "===============" << endl;

    cout << "当货币很少出现重复，dp2比dp3有常数时间优势" << endl;
    cout << "当货币大量出现重复，dp3时间复杂度明显优于dp2" << endl;
    cout << "dp3的优化用到了窗口最小值的更新结构" << endl;

    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126
    • 127
    • 128
    • 129
    • 130
    • 131
    • 132
    • 133
    • 134
    • 135
    • 136
    • 137
    • 138
    • 139
    • 140
    • 141
    • 142
    • 143
    • 144
    • 145
    • 146
    • 147
    • 148
    • 149
    • 150
    • 151
    • 152
    • 153
    • 154
    • 155
    • 156
    • 157
    • 158
    • 159
    • 160
    • 161
    • 162
    • 163
    • 164
    • 165
    • 166
    • 167
    • 168
    • 169
    • 170
    • 171
    • 172
    • 173
    • 174
    • 175
    • 176
    • 177
    • 178
    • 179
    • 180
    • 181
    • 182
    • 183
    • 184
    • 185
    • 186
    • 187
    • 188
    • 189
    • 190
    • 191
    • 192
    • 193
    • 194
    • 195
    • 196
    • 197
    • 198
    • 199
    • 200
    • 201
    • 202
    • 203
    • 204
    • 205
    • 206
    • 207
    • 208
    • 209
    • 210
    • 211
    • 212
    • 213
    • 214
    • 215
    • 216
    • 217
    • 218
    • 219
    • 220
    • 221
    • 222
    • 223
    • 224
    • 225
    • 226
    • 227
    • 228
    • 229
    • 230
    • 231
    • 232
    • 233
    • 234
    • 235
    • 236
    • 237
    • 238
    • 239
    • 240
    • 241
    • 242
    • 243
    • 244
    • 245
    • 246
    • 247
    • 248
    • 249
    • 250
    • 251
    • 252
    • 253
    • 254
    • 255
    • 256
    • 257
    • 258
    • 259
    • 260
    • 261
    • 262
    • 263
    • 264
    • 265
    • 266
    • 267
    • 268
    • 269
    • 270
    • 271
    • 272
    • 273
    • 274
    • 275
    • 276
    • 277
    • 278
    • 279
    • 280
    • 281
    • 282
    • 283
    • 284
    • 285
    • 286
    • 287
    • 288
    • 289
    • 290
    • 291
    • 292
    • 293
    • 294
    • 295
    • 296
    • 297

    Java 版

    public class Code04_MinCoinsOnePaper {

	public static int minCoins(int[] arr, int aim) {
		return process(arr, 0, aim);
	}
	
    //经典方法：货币不去重，讨论每张货币用和不用的情况
    //暴力递归
	public static int process(int[] arr, int index, int rest) {
		if (rest < 0) {
			return Integer.MAX_VALUE;
		}
		if (index == arr.length) {
			return rest == 0 ? 0 : Integer.MAX_VALUE;
		} else {
			int p1 = process(arr, index + 1, rest);
			int p2 = process(arr, index + 1, rest - arr[index]);
			if (p2 != Integer.MAX_VALUE) {
				p2++;
			}
			return Math.min(p1, p2);
		}
	}

    //暴力递归改成的动态规划
	// dp1时间复杂度为：O(arr长度 * aim)
	public static int dp1(int[] arr, int aim) {
		if (aim == 0) {
			return 0;
		}
		int N = arr.length;
		int[][] dp = new int[N + 1][aim + 1];
		dp[N][0] = 0;
		for (int j = 1; j <= aim; j++) {
			dp[N][j] = Integer.MAX_VALUE;
		}
		for (int index = N - 1; index >= 0; index--) {
			for (int rest = 0; rest <= aim; rest++) {
				int p1 = dp[index + 1][rest];
				int p2 = rest - arr[index] >= 0 ? dp[index + 1][rest - arr[index]] : Integer.MAX_VALUE;
				if (p2 != Integer.MAX_VALUE) {
					p2++;
				}
				dp[index][rest] = Math.min(p1, p2);
			}
		}
		return dp[0][aim];
	}

	public static class Info {
		public int[] coins; //所有货币去重后的数组
		public int[] zhangs; //每种货币的张数

		public Info(int[] c, int[] z) {
			coins = c;
			zhangs = z;
		}
	}

	public static Info getInfo(int[] arr) {
		HashMap<Integer, Integer> counts = new HashMap<>();
		for (int value : arr) {
			if (!counts.containsKey(value)) {
				counts.put(value, 1);
			} else {
				counts.put(value, counts.get(value) + 1);
			}
		}
		int N = counts.size();
		int[] coins = new int[N];
		int[] zhangs = new int[N];
		int index = 0;
		for (Entry<Integer, Integer> entry : counts.entrySet()) {
			coins[index] = entry.getKey();
			zhangs[index++] = entry.getValue();
		}
		return new Info(coins, zhangs);
	}

	// dp2时间复杂度为：O(arr长度) + O(货币种数 * aim * 每种货币的平均张数)
	public static int dp2(int[] arr, int aim) {
		if (aim == 0) {
			return 0;
		}
		// 得到info时间复杂度O(arr长度)
		Info info = getInfo(arr);
		int[] coins = info.coins;
		int[] zhangs = info.zhangs;
		int N = coins.length;
		int[][] dp = new int[N + 1][aim + 1];
		dp[N][0] = 0;
		for (int j = 1; j <= aim; j++) {
			dp[N][j] = Integer.MAX_VALUE;
		}
		// 这三层for循环，时间复杂度为O(货币种数 * aim * 每种货币的平均张数)
		for (int index = N - 1; index >= 0; index--) {
			for (int rest = 0; rest <= aim; rest++) {
				dp[index][rest] = dp[index + 1][rest];
				for (int zhang = 1; zhang * coins[index] <= aim && zhang <= zhangs[index]; zhang++) { //枚举行为
					if (rest - zhang * coins[index] >= 0
							&& dp[index + 1][rest - zhang * coins[index]] != Integer.MAX_VALUE) {
						dp[index][rest] = Math.min(dp[index][rest], zhang + dp[index + 1][rest - zhang * coins[index]]);
					}
				}
			}
		}
		return dp[0][aim];
	}

	// dp3时间复杂度为：O(arr长度) + O(货币种数 * aim)
	// 优化需要用到窗口内最小值的更新结构
	public static int dp3(int[] arr, int aim) {
		if (aim == 0) {
			return 0;
		}
		// 得到info时间复杂度O(arr长度)
		Info info = getInfo(arr);
		int[] c = info.coins;
		int[] z = info.zhangs;
		int N = c.length;
		int[][] dp = new int[N + 1][aim + 1];
		dp[N][0] = 0;
		for (int j = 1; j <= aim; j++) {
			dp[N][j] = Integer.MAX_VALUE;
		}
		// 虽然是嵌套了很多循环，但是时间复杂度为O(货币种数 * aim)
		// 因为用了窗口内最小值的更新结构
		for (int i = N - 1; i >= 0; i--) {
            //例如目标货币是30元，而当前货币面值是7元，则先填0，7, 14, 21, 28；然后填1, 8, 15, 22, 29... 分组填
			for (int mod = 0; mod < Math.min(aim + 1, c[i]); mod++) { 
				// 当前面值 X
				// mod  mod + x   mod + 2*x   mod + 3 * x
				LinkedList<Integer> w = new LinkedList<>();
				w.add(mod);
				dp[i][mod] = dp[i + 1][mod];
				for (int r = mod + c[i]; r <= aim; r += c[i]) {
					while (!w.isEmpty() && (dp[i + 1][w.peekLast()] == Integer.MAX_VALUE
							|| dp[i + 1][w.peekLast()] + compensate(w.peekLast(), r, c[i]) >= dp[i + 1][r])) { //入队列的时候要跟补偿后的张数进行比较
						w.pollLast();
					}
					w.addLast(r);
					int overdue = r - c[i] * (z[i] + 1);
					if (w.peekFirst() == overdue) {
						w.pollFirst();
					}
					dp[i][r] = dp[i + 1][w.peekFirst()] + compensate(w.peekFirst(), r, c[i]); //得到最后结果的时候也要进行补偿
				}
			}
		}
		return dp[0][aim];
	}

	public static int compensate(int pre, int cur, int coin) {
		return (cur - pre) / coin;
	}

	// 为了测试
	public static int[] randomArray(int N, int maxValue) {
		int[] arr = new int[N];
		for (int i = 0; i < N; i++) {
			arr[i] = (int) (Math.random() * maxValue) + 1;
		}
		return arr;
	}

	// 为了测试
	public static void printArray(int[] arr) {
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// 为了测试
	public static void main(String[] args) {
		int maxLen = 20;
		int maxValue = 30;
		int testTime = 300000;
		System.out.println("功能测试开始");
		for (int i = 0; i < testTime; i++) {
			int N = (int) (Math.random() * maxLen);
			int[] arr = randomArray(N, maxValue);
			int aim = (int) (Math.random() * maxValue);
			int ans1 = minCoins(arr, aim);
			int ans2 = dp1(arr, aim);
			int ans3 = dp2(arr, aim);
			int ans4 = dp3(arr, aim);
			if (ans1 != ans2 || ans3 != ans4 || ans1 != ans3) {
				System.out.println("Oops!");
				printArray(arr);
				System.out.println(aim);
				System.out.println(ans1);
				System.out.println(ans2);
				System.out.println(ans3);
				System.out.println(ans4);
				break;
			}
		}
		System.out.println("功能测试结束");

		System.out.println("==========");

		int aim = 0;
		int[] arr = null;
		long start;
		long end;
		int ans2;
		int ans3;

		System.out.println("性能测试开始");
		maxLen = 30000;
		maxValue = 20;
		aim = 60000;
		arr = randomArray(maxLen, maxValue);

		start = System.currentTimeMillis();
		ans2 = dp2(arr, aim);
		end = System.currentTimeMillis();
		System.out.println("dp2答案 : " + ans2 + ", dp2运行时间 : " + (end - start) + " ms");

		start = System.currentTimeMillis();
		ans3 = dp3(arr, aim);
		end = System.currentTimeMillis();
		System.out.println("dp3答案 : " + ans3 + ", dp3运行时间 : " + (end - start) + " ms");
		System.out.println("性能测试结束");

		System.out.println("===========");

		System.out.println("货币大量重复出现情况下，");
		System.out.println("大数据量测试dp3开始");
		maxLen = 20000000;
		aim = 10000;
		maxValue = 10000;
		arr = randomArray(maxLen, maxValue);
		start = System.currentTimeMillis();
		ans3 = dp3(arr, aim);
		end = System.currentTimeMillis();
		System.out.println("dp3运行时间 : " + (end - start) + " ms");
		System.out.println("大数据量测试dp3结束");

		System.out.println("===========");

		System.out.println("当货币很少出现重复，dp2比dp3有常数时间优势");
		System.out.println("当货币大量出现重复，dp3时间复杂度明显优于dp2");
		System.out.println("dp3的优化用到了窗口内最小值的更新结构");
	}
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126
    • 127
    • 128
    • 129
    • 130
    • 131
    • 132
    • 133
    • 134
    • 135
    • 136
    • 137
    • 138
    • 139
    • 140
    • 141
    • 142
    • 143
    • 144
    • 145
    • 146
    • 147
    • 148
    • 149
    • 150
    • 151
    • 152
    • 153
    • 154
    • 155
    • 156
    • 157
    • 158
    • 159
    • 160
    • 161
    • 162
    • 163
    • 164
    • 165
    • 166
    • 167
    • 168
    • 169
    • 170
    • 171
    • 172
    • 173
    • 174
    • 175
    • 176
    • 177
    • 178
    • 179
    • 180
    • 181
    • 182
    • 183
    • 184
    • 185
    • 186
    • 187
    • 188
    • 189
    • 190
    • 191
    • 192
    • 193
    • 194
    • 195
    • 196
    • 197
    • 198
    • 199
    • 200
    • 201
    • 202
    • 203
    • 204
    • 205
    • 206
    • 207
    • 208
    • 209
    • 210
    • 211
    • 212
    • 213
    • 214
    • 215
    • 216
    • 217
    • 218
    • 219
    • 220
    • 221
    • 222
    • 223
    • 224
    • 225
    • 226
    • 227
    • 228
    • 229
    • 230
    • 231
    • 232
    • 233
    • 234
    • 235
    • 236
    • 237
    • 238
    • 239
    • 240
    • 241
    • 242
    • 243
    • 244
    • 245
    • 246
    • 247
  • 相关阅读:
    Git仓库迁移记录
    2.区块链系列之部署合约
    外汇天眼：美联储如预期再次加息75个基点 并誓言进一步加息以对抗通胀
    【RuoYi-Vue-Plus】学习笔记 34 - Redisson（九）RedissonMapCache 缓存流程分析（下）（Lua 脚本）
    工业自动化应用智能制造技术有哪些作用？
    什么是“2 Way SSL”以及它是如何工作的？
    华为vrrp+mstp+dhcp配置案例
    flutter开发实战-应用更新apk下载、安装apk、启动应用实现
    MybatisPlus常用设置
    C++二级指针的指向与解引用
  • 原文地址：https://blog.csdn.net/u011386173/article/details/127870057