-
信息熵,交叉熵,KL散度,互信息一网打尽
talk
一直以来都是自己有时候 想去搞明白就搜搜博客看,模棱两可,记忆也比较模糊,这次直接较为系统的记录一下,之后忘了也能看看~
1. 信息熵
这个概念是从信息论出现的,是香农定义的,根据事件发生的概率进行定义。具体上:
事件发生概率越小,包含的信息量越大。- 1
意思就是,很少发生的事件,会让人surprise,维基百科Entropy很好的解释了这个,当时看到surprise开始不理解,查了之后具体就是 等价于 信息。 因为香农认为让人惊奇的事情包含信息量大,如 太阳每天东边升起,没什么信息量=0(必然事件,概率=1),中彩票,概率小,信息量大。
公式是: 根据对数定义,和事件发生的概率 是 成反比的。log满足了 p=1,信息量=0
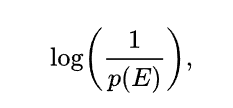
一般就是这两种形式,对数 分数或者-log, 信息量有时候也被称为 编码长度,方便理解
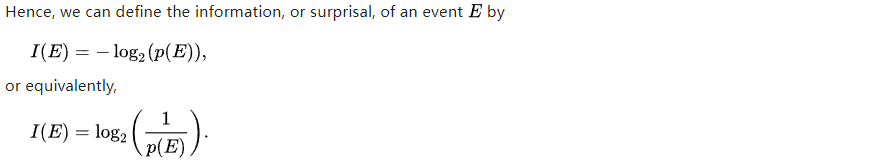
熵被定义为= 相应事件的概率*事件的信息量
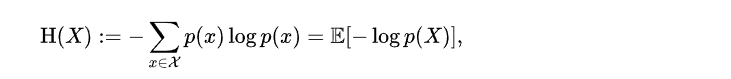
2. 交叉熵 wiki
含义: 数据是基于一个wrong的 q的编码长度 然而 数据真正是 遵循一个p分布。

p的期望*基于q的编码长度。 p一般是真实的数据分布概率,q的编码长度是 模型输出的,根据交叉熵,能够对模型输出的q一直进行调整,当p和q的 编码一致时,损失最小。(多分类,one-hot标签情况下)
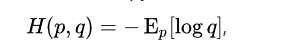
知乎有个分类的例子去计算 ,真实标签作为p的期望,所得的概率,计算出编码长度和p的期望进行计算交叉熵。3. KL散度
性质:不对称
衡量两个分布之间的距离,但这个不是常见的距离,这也是被称为散度,而不是距离的原因。 因为KL散度不符合距离的对称性,即KL(P||Q) != KL(Q||P) . 同时不满足三角不等式,因此不是距离,而是 divergence
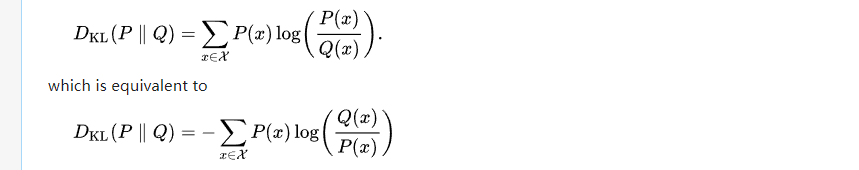
上面是离散形式,底下是连续变量之间的。 通过离散形式的第二项(变成类似熵形式),可以看出KL散度=交叉熵-熵,这就是多分类里面常用交叉熵来代替KL散度的原因,因为KL散度第二项熵是 常量,因此可以省略。
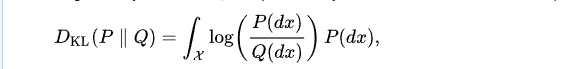
解释:
KL散度本质上是 采用Q编码系统来解码 基于P编码系统的数据 所 额外需要 进行传输 的数据,即就是 交叉熵(Q解码P)-熵(P解码P)。当两者分布相同,交叉熵 H(P,Q)-熵H(P) =0, 即 通过Q解码数据P 和 通过P解码P一样。
这里 知乎或者csdn 有部分解答,但是很多都说错了。他们都是说 基于P去解码Q,只有一个对的,和wiki一样
这个链接是错的,就是底下这个 他说 是 基于P编码 Q

这个是对的KL散度解释, 两个不同之处就在于 是Q去编码P,开始一直疑惑这里到底谁是,

维基百科 这里很直接指出了:KL= 采用一个Q编码系统而不是 P编码系统 来去编码 P的数据 的差值,也就是 交叉熵-熵

4. 互信息 wiki
这个Venn图经典也直观,两个圆相交的区域 (紫色)就是互信息。性质:非负,对称。

互信息有很多种定义形式:-
边缘分布和联合分布乘积之间的KL散度
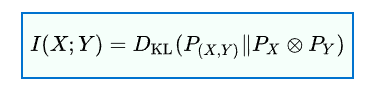
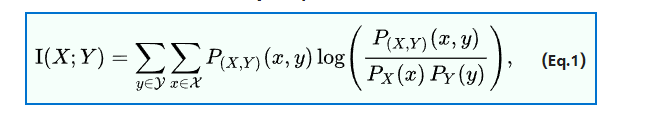
-
熵-条件熵 。
这里从Venn图就可以看出来,紫色=左侧圆(熵)-左侧红色(条件熵)- 1
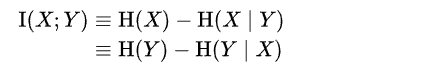
-
2个熵-联合熵
这里先指出:联合熵=上面Venn图中所有有颜色的区域,即两个圆面积-1*相交区域(紫色)。 因此从 Venn图看出 MI= H(x)+H(Y) - H(X,Y)。 前面两项把中间算2次-后面这项只算一次,就=中间紫色区域- 1
- 2
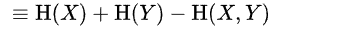
-
联合熵-2个条件熵
紫色=总面积-左边红-右边蓝- 1
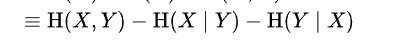
Proof:
从1推其余的 wiki里面的
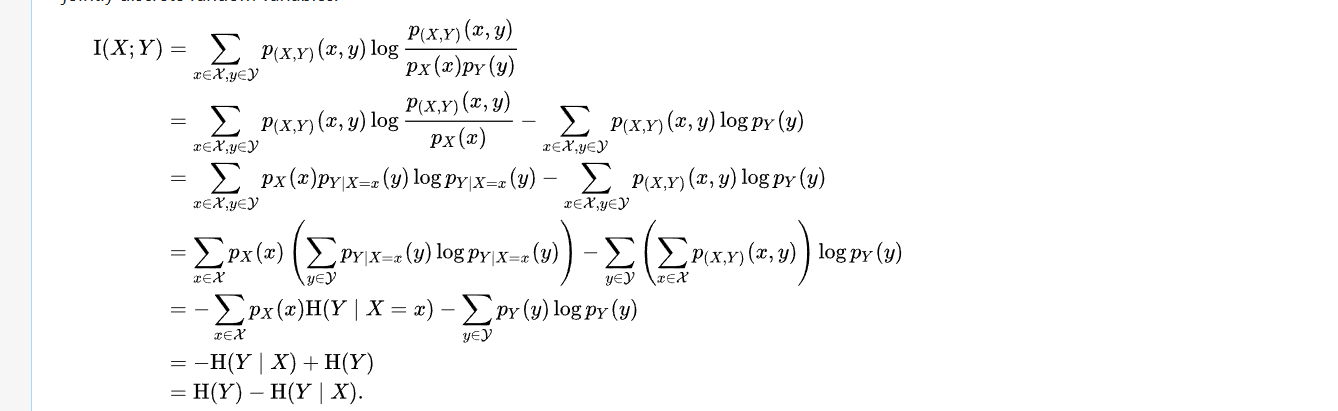
从 其余的推1推导
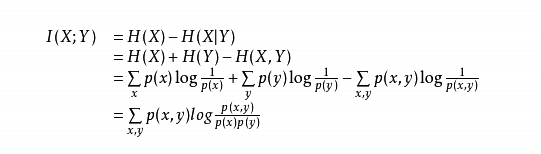
-
相关阅读:
感悟:一个小小的摄像头APP,也解决了很多BUG
在物理计算机上安装Linux的方法,台式机安装CentOS时报错dracut-initqueue timeout解决办法
ZZULIOJ:1158: 又是排序(指针专题)
CSS Layout
【无标题】360压缩软件怎么用?超级好用!
pnpm项目内网迁移技巧
飞书开发学习笔记(七)-添加机器人及发送webhook消息
Jenkins配置远程服务器之Publish over SSH、SSH Servers
Word控件Spire.Doc 【图像形状】教程(5) 如何在 C# 中将文本环绕在图像周围
Python Day3 爬虫-数据接口和selenium基础
- 原文地址:https://blog.csdn.net/qq_40926715/article/details/127830719