刷题日记【第十一篇】-笔试必刷题【小易的升级之路+找出字符串中第一个只出现一次的字符+微信红包+计算字符串的编辑距离】

1.计算字符串的编辑距离【动态规划编程题】

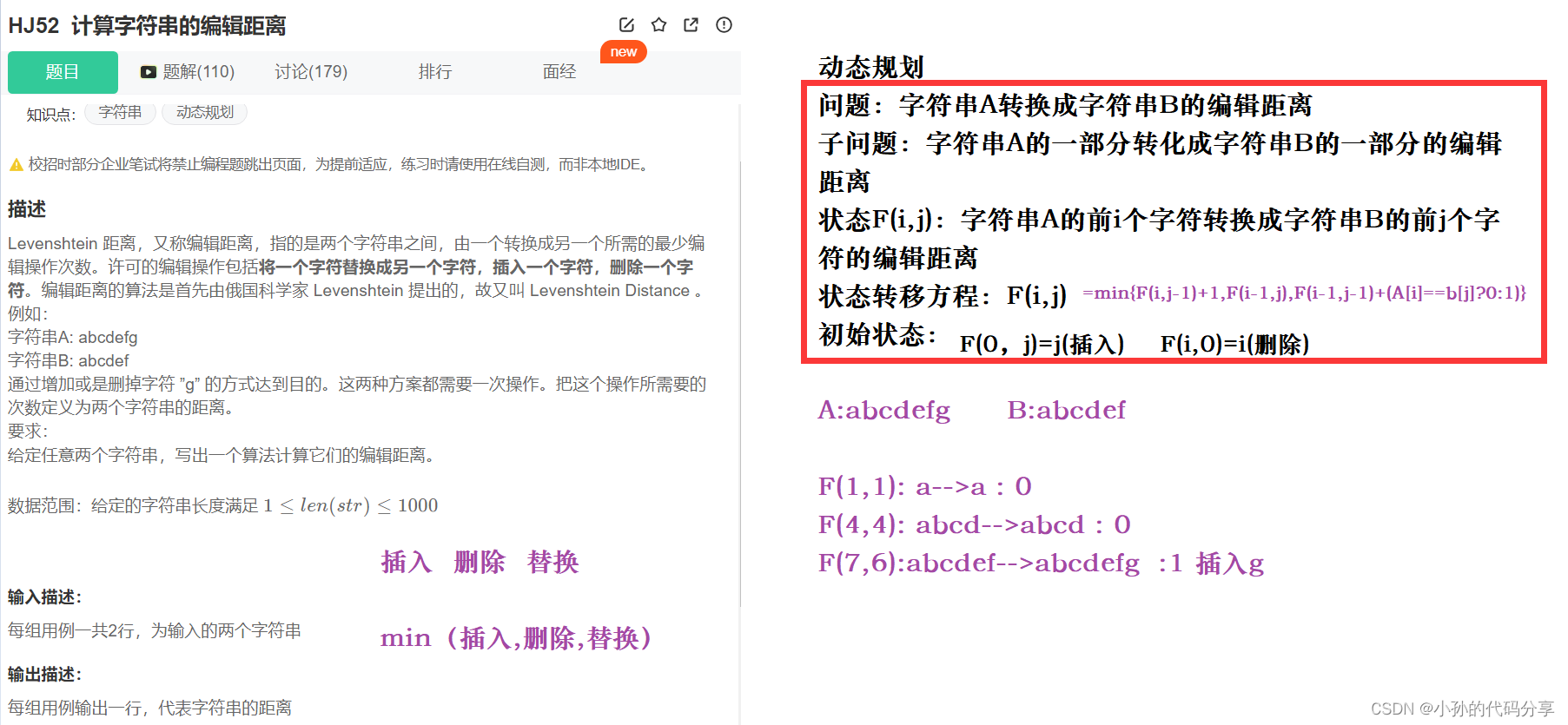
import java.util.Scanner;
import  java.io.*;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {


    public static void main(String args[])  throws Exception{
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in)); 
        String str1 ;
        while((str1=reader.readLine())!=null){
            String str2 = reader.readLine();
            System.out.println(getDistance(str1,str2));
        }

    }


    public  static int getDistance(String str1, String str2) {

        char[] ch1 = str1.toCharArray();
        char[] ch2 =  str2.toCharArray();

        int len1  = ch1.length;
        int  len2  = ch2.length;
        //定义一个矩阵
        int[][] dist = new  int[len1 + 1][len2 + 1];
        //初始状态 F(i,0) = i F(0,j) = j
        for (int i = 0; i <= len1; ++i) {
            dist[i][0] = i;
        }
        for (int j = 0; j <= len2; ++j) {
            dist[0][j] = j;
        }

        for (int i = 1; i <= len1; ++i) {
            for (int j = 1; j <= len2; ++j) {
                //F[i,j] = min(F(i-j,j)+1,F(i,j-1)+1,F(i-1,j-1)+(ch1[i]==ch2[j]?0:1))
                //          插入           删除                替换
                dist[i][j] = Math.min(dist[i - 1][j] + 1, dist[i][j - 1] + 1);
                //在和替换比较
                if (ch1[i - 1] == ch2[j - 1]) {
                    dist[i][j] = Math.min(dist[i ][j], dist[i - 1][j - 1]);
                } else {
                    dist[i][j] = Math.min(dist[i ][j], dist[i - 1][j - 1]+1);
                }
            }

        }
        return dist[len1][len2];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

2.微信红包

import java.util.*;

public class Gift {
    public int getValue(int[] gifts, int n) {
        // write code here
        int mid = gifts.length / 2;
        int count = 0;
        for (int i = 0; i < gifts.length; i++) {
            if (gifts[i] == gifts[mid]) {
                count++;
            }
        }
        if (count > mid) {
            return gifts[mid];
        }
        return 0 ;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.找出字符串中第一个只出现一次的字符

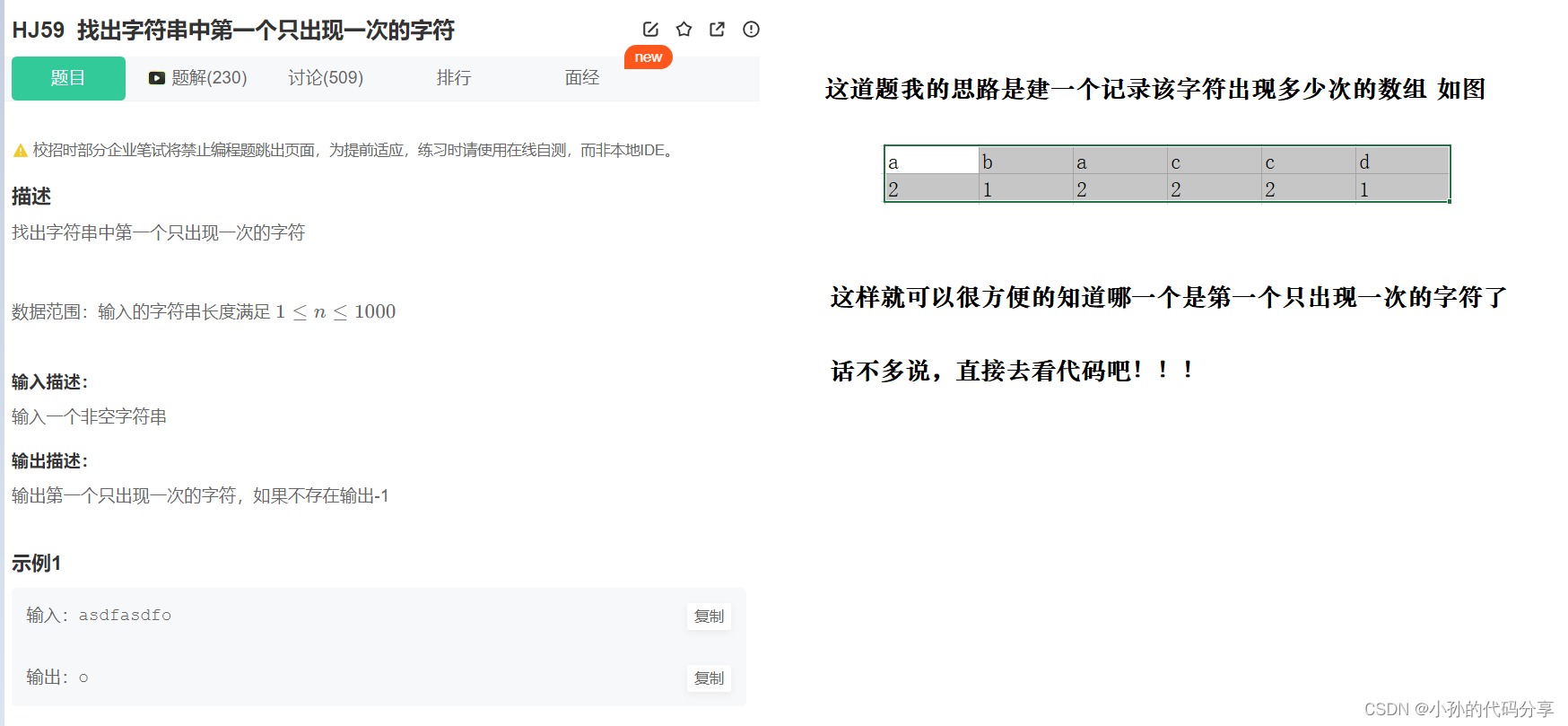
import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        String str = in.nextLine();
        int[] arr = new int[str.length()];
        for(int i=0;i<str.length();i++){
            arr[i]= count(str,str.charAt(i));
        }
        for(int j =0;j<arr.length;j++){
            if(arr[j]==1){
                System.out.println(str.charAt(j));
                break;
            }

            if(none(arr)==-1){
                System.out.println(-1);
                break;
            }
        }
    }
    public  static int none(int[] arr){
        int count = 0;
        for(int i= 0;i<arr.length;i++){
            if(arr[i]!=1){
                count++;
            }
        }
        if(count==arr.length){
            return -1;
        }
        return 0;
    }

    public  static int count(String str,char ch){
        int count = 0;
        for(int i =0;i<str.length();i++){
            if(str.charAt(i)==ch){
                count++;
            }
        }
        return count;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

4.小易的升级之路

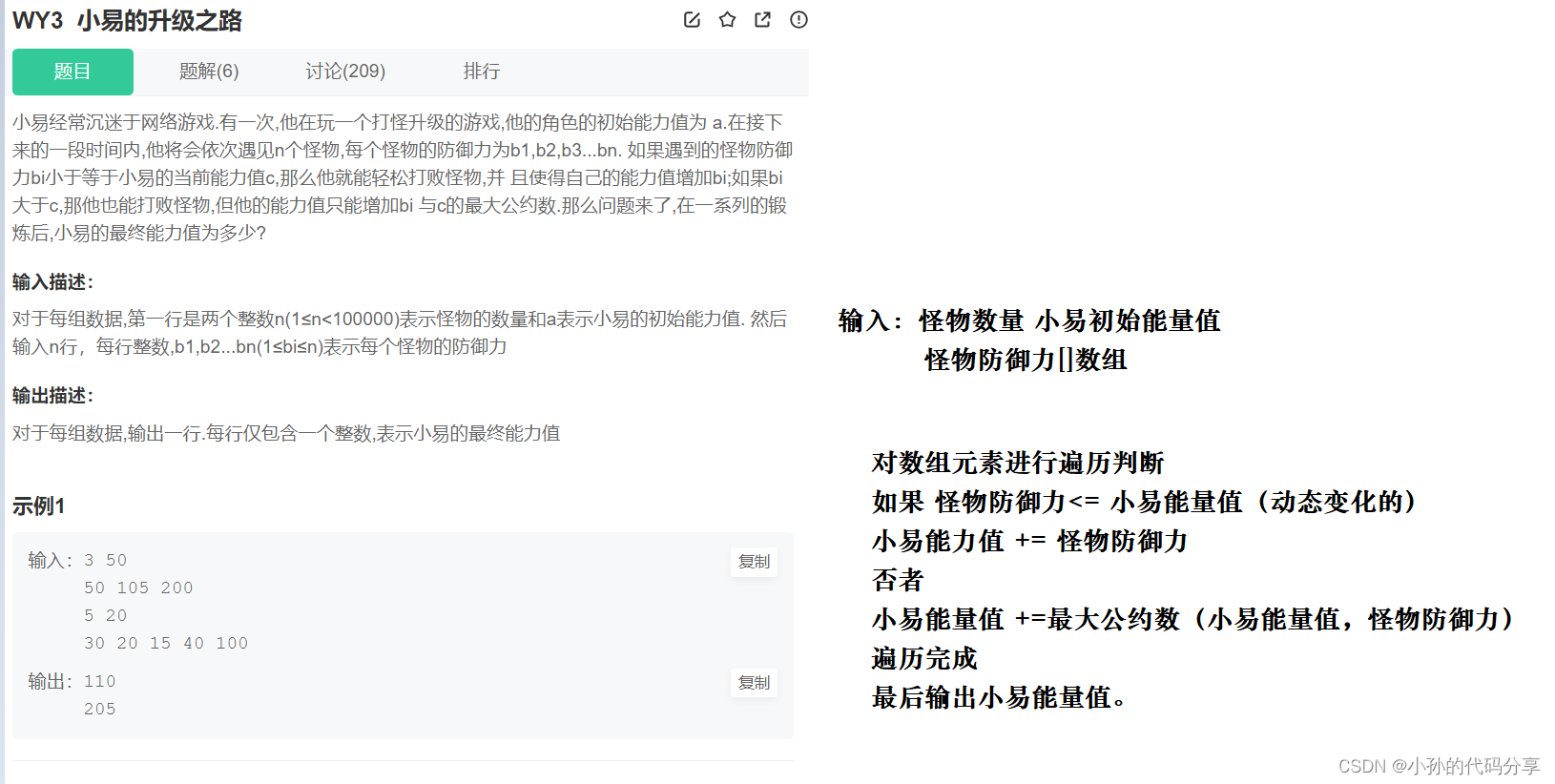
import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextInt()) { // 注意 while 处理多个 case
            int n = in.nextInt();
            int c = in.nextInt();
            int[] arr = new int[n];
            for (int i = 0; i < n; i++) {
                arr[i] = in.nextInt();
            }

            for (int i = 0; i < n; i++) {
                if (arr[i] <= c) {
                    c += arr[i];
                } else {
                    c += zdgy(c, arr[i]);
                }
            }
            System.out.println(c);
        }

    }
    public static int zdgy(int c, int arr) {
        for (int i = c; i > 0; i--) {
            if (arr % i == 0 && c % i == 0) {
                return i;
            }
        }
        return 0 ;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

4.数据结构中具有记忆功能的是【栈】

下列数据结构具有记忆功能的是? C
A. 队列 B. 循环队列 C. 栈 D. 顺序表
记忆功能比如, 浏览器的回退功能,文本编辑器的撤销功能,都属于记忆功能
栈的LIFO特性,A函数调用B函数,B函数调用C函数,然后最后一层一层返回,这也具有记忆功能

5.递归程序的优化一般为 【尾递归优化】

对递归程序的优化的一般的手段为(A)

A. 尾递归优化       B. 循环优化        C. 堆栈优化            D. 停止值优化

比如快速排序和归并排序,在递归的终止条件是 l 是区间最左侧,r 是区间最右侧

//终止条件

(l >= r){return ;}

//在递归终止条件处进行优化

//当区间个数较小时,采用插入排序来优化

(r - l <= 15)  --->  采用插入排序

所以这种对递归的优化一般都是 尾递归优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

6.时间复杂度的判断

A 红黑树插入操作的平均时间复杂度为O(logn)，最坏时间复杂度为O(logn)
B B+树插入操作的平均时间复杂度为O(logn)，最坏时间复杂度为O(logn)
C Hash表插入操作的平均时间复杂度为O(logn)，最坏时间复杂度为O(n)
D 排序链表插入操作的平均时间复杂度为O(n)，最坏时间复杂度为O(n)
1
2
3
4

由图可知，Hash表插入操作的平均时间复杂度为O(1)，最坏时间复杂度为O(1)

7.为提高散列（Hash）表的查找效率，可以采取的正确措施是（II,III ）

Ⅰ．增大装填（载）因子
Ⅱ．设计冲突（碰撞）少的散列函数
Ⅲ．处理冲突（碰撞）时避免产生聚集（堆积）现象
1
2
3

散列表的查找效率取决于：散列函数、处理冲突的方法和装填因子。 冲突的产生概率与装填因子成正比，故错。
采取合适的冲突处理方法可以避免聚集现象，也提高查找效率。