实验八 数据处理与多项式处理（matlab）

实验八 数据处理与多项式处理

1.1实验目的

1.2实验内容

1.3流程图

1.4程序清单

1.5运行结果及分析

1.6实验的收获与体会

1.1实验目的

1，掌握数据统计和分析的方法；

2，掌握数值插值与曲线拟合的方法；

3，掌握多项式计算的常用运算。

1.2实验内容

 

 

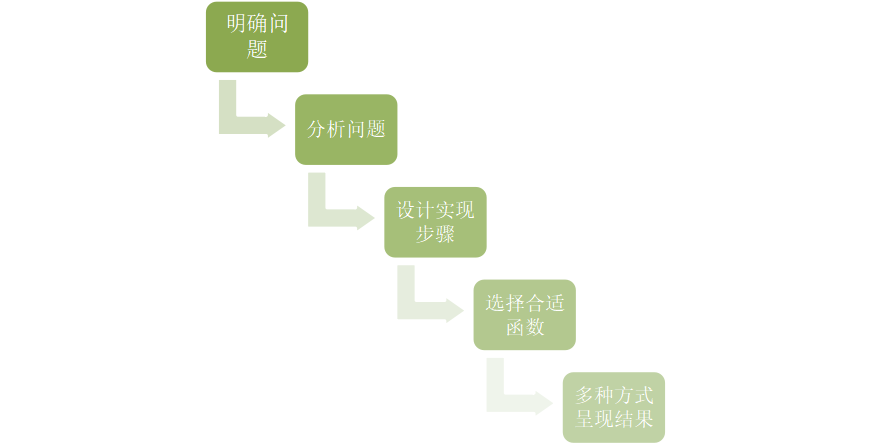
1.3流程图

 

1.4程序清单

clc

clear

%% 1

A=rand(30000,1);

pjz=mean(A)

bzfc=std(A)

zdz=max(A)

zxz=min(A)

bfb=length(find(A>0.5))/30000

%% 2

P=45+(95-45)*rand(100,5)

[Y,U]=max(P)

[Y1,U1]=min(P)

mean(P)

std(P,0,1)

K=sum(P,2)

[E,F]=max(K)

[E1,F1]=min(K)

[zcj,xsxh]=-sort(-K,1)

%% 3

h=6:2:18;

t1=[18 20 22 25 30 28 24]

t2=[15 19 24 28 34 32 30]

h2=6.5:2:17.5;

t1c=interp1(h,t1,h2,'spline')

t2c=interp1(h,t2,h2,'spline')

%% 4

x=1:10:101

lgx=[0 1.0414 1.3222 1.4914 1.6128 1.7076 1.7853 1.8513 1.9085 1.959 2.0043]

P=polyfit(x,lgx,5)

Y1=polyval(P,x)

plot(x,lgx,':o',x,Y1,'-*')

legend('lgx','多项式')

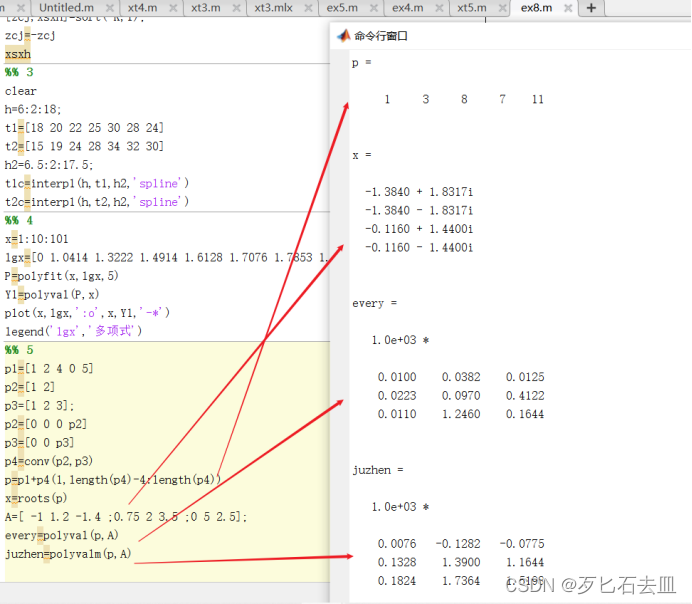
%% 5

p1=[1 2 4 0 5]

p2=[1 2]

p3=[1 2 3];

p2=[0 0 0 p2]

p3=[0 0 p3]

p4=conv(p2,p3)

p=p1+p4(1,length(p4)-4:length(p4))

x=roots(p)

A=[ -1 1.2 -1.4 ;0.75 2 3.5 ;0 5 2.5];

every=polyval(p,A)

juzhen=polyvalm(p,A)

1.5运行结果及分析

1． 

 

2.

 

3．

 

 

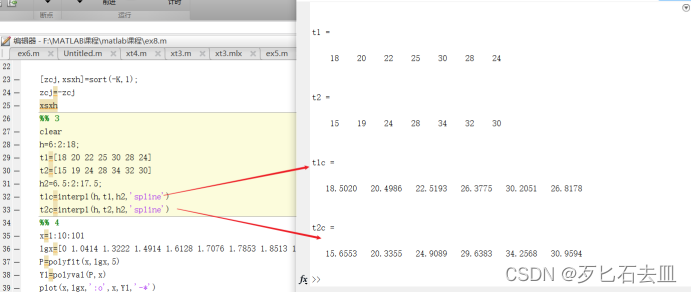
4

 

5．

 

1.6实验的收获与体会

本次实验过后，我掌握了数据统计和分析的方法和数值插值与曲线拟合的方法，以及多项式计算的常用运算。

这次实验对接的是实际问题，可以对实际的数据进行处理。得到一些数据然后输入matlab里面，无论是取平均值，标准差还是做各种差值处理，matlab里面都有相应的函数可供直接调用，为我们省下不少时间，减弱了自己计算的繁琐步骤。

同时matlab进行的数值计算对于其他数学问题也非常有帮助，在别的问题里面需要花费10-20分钟的时间进行列式和计算的工作，放在matlab里面简简单单一个函数，一行代码就可以在1分钟内解决，而且计算精度和准确度得到了保障。

总之，经过这次实验收获很大，对学习帮助很大。