【math】Hiden Markov Model 隐马尔可夫模型了解

Introduction to Hidden Markov Model

Introduction

• Markov chains were first introduced in 1906 by Andrey Markov
• HMM was developed by L. E. Baum and coworkers in the 1960s
• HMM is simplest dynamic Bayesian network and a directed graphic model
• Application: speech recognition, PageRank(Google), DNA analysis, …

Markov chain

A Markov chain is “a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event”.

Space or time can be either discrete(𝑋_𝑡:t=0, 1, 2,…) or continuous(𝑋_𝑡:t≥0). (we will focus on Markov chains in discrete space an time)

Example for Markov chain：

• transition matrix 𝑄 :
• 5-step transition matrix is 𝑄^5 :
  

Hidden Markov Model(HMM)

HMM is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved (i.e. hidden) states.

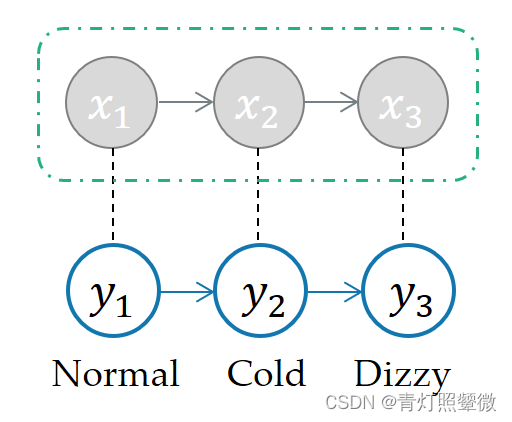
State: x = (x1, x2, x3) ; 
Observation: y = (y1, y2, y3);
Transition matrix: A = (aij); 
Emission matrix: B = (bij)
1
2
3
4

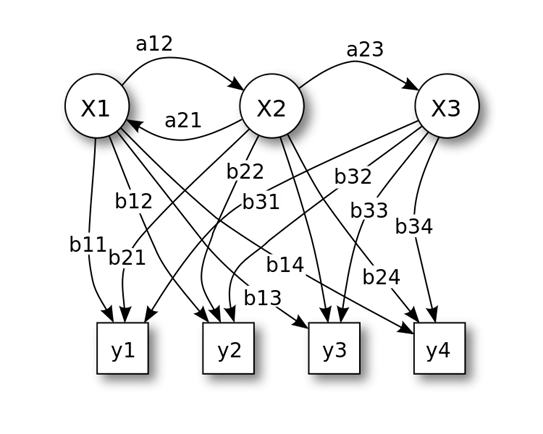
Example:

Three Questions

• Given the model 𝜆=[𝐴, 𝐵,𝜋], how to calculate the probability of producing the observation 𝒚={𝑦${}_1$,𝑦${}_2$,…,𝑦${}_n$ | 𝑦${}_i$∈𝑂}? In other words, how to evaluate the matching degree between the model and the observation ?
• Given the model 𝜆=[𝐴, 𝐵,𝜋] and the observation 𝒚={𝑦${}_1$,𝑦${}_2$,…,𝑦${}_n$| 𝑦${}_i$∈𝑂}, how to find most probable state 𝒙={𝑥${}_1$,𝑥${}_2$,…,𝑥${}_n$ |𝑥${}_i$∈𝑆} ? In other words, how to infer the hidden state from the observation ?
• Given the observation 𝒚={𝑦${}_1$,𝑦${}_2$,…,𝑦${}_n$ | 𝑦${}_i$∈𝑂}, how to adjust model parameters 𝜆=[𝐴, 𝐵,𝜋] to maximize to the probability 𝑃(𝒚│𝜆) ? In other words, how to train the model to describe the observation more accurately ?

Q1: evaluate problem – Forward algorithm

Q1: how to evaluate the matching degree between the model and the observation ? ( forward algorithm)

• the probability of observing event 𝑦${}_1$: 𝑃${}_{i0}$ = 𝑃${}_i$ (𝑂=𝑦${}_1$) = 𝜋${}_i{b}_{1i}$
• the probability of observing event 𝑦${}_{j+1}$ (𝑗≥1): 𝑃${}_{i}j$=𝑏${}_{j,i+1}$ ∑${}_k$𝑃${}_{i,j-1}$ 𝑎${}_{ij}$
• 𝑃(𝒚)=∑${}_k$ 𝑃${}_{ij}$∗𝑎${}_{j0}$
  

Q2: decode problem – Viterbi algorithm

Q2: how to infer the hidden state from the observation ? (Viterbi algorithm)

Observation 𝒚=(𝑦${}_1$, 𝑦${}_2$,…, 𝑦${}_T$), initial prob. 𝝅=(𝜋${}_1$,𝜋${}_2$,…, 𝜋${}_K$), transition matrix 𝐴, emission matrix 𝐵.

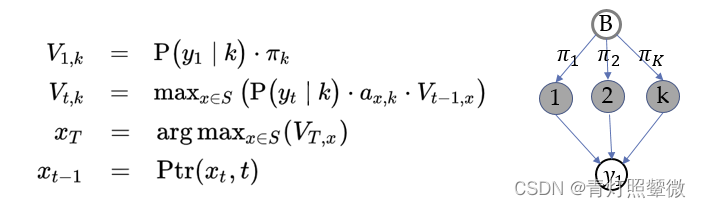
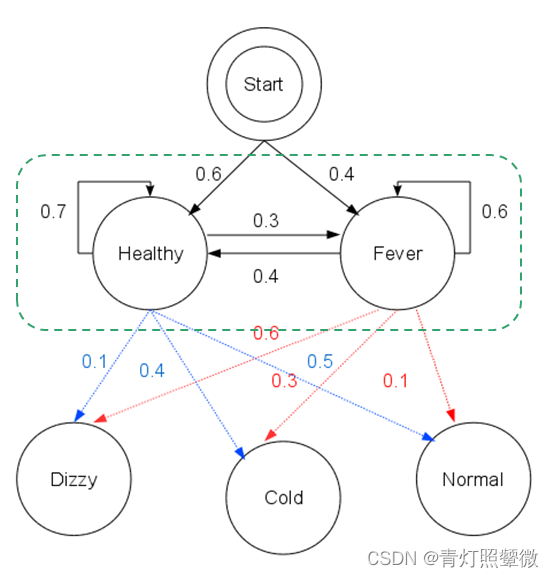
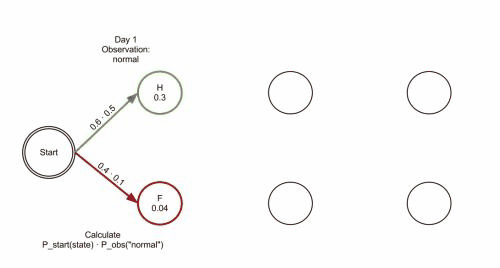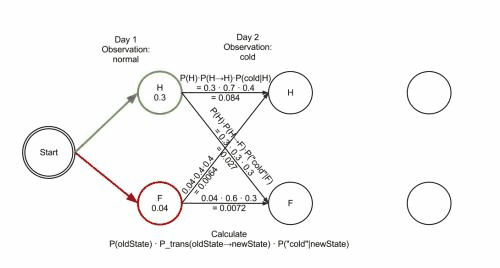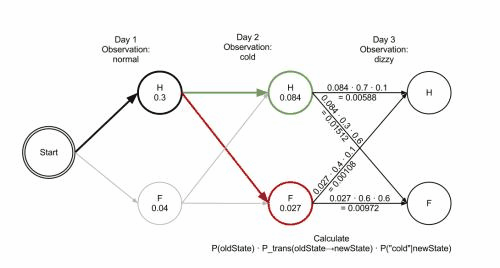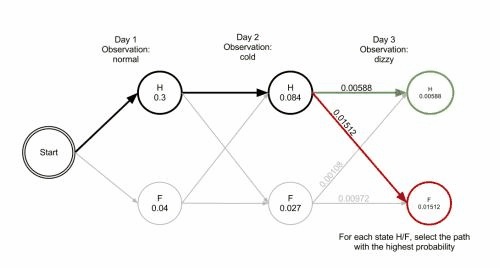
Viterbi algorithm(optimal solution) backtracking method; It retains the optimal solution of each choice in the previous step and finds the optimal selection path through the backtracking method.

Example:

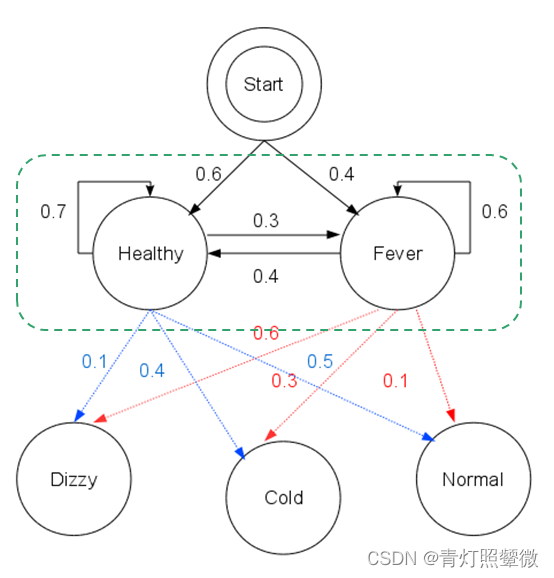
• The observation 𝒚={“′Normal′, ′Cold′, ′Dizzy′” } , 𝜆=[𝐴, 𝐵,𝜋], the hidden state 𝒙={𝑥${}_1$,𝑥${}_2$,𝑥${}_3$}= ?
  
  

Q3: learn problem – Baum-Welch algorithm

Q3: how to train the model to describe the observation more accurately ? (Baum-Welch algorithm)

The Baum–Welch algorithm uses the well known EM algorithm to find the maximum likelihood estimate of the parameters of a hidden Markov model given a set of observed feature vectors.


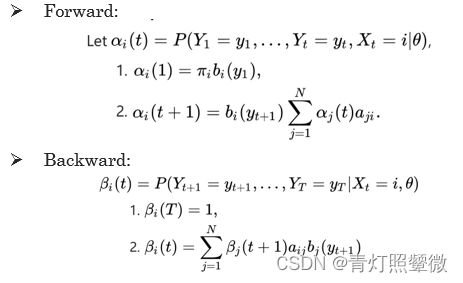
Baum–Welch algorithm(forward-backward alg.) It approximates the optimal parameters through iteration.

• (1) Likelihood function :
  𝑙𝑜𝑔𝑃(Y,𝐼|𝜆)
• (2) Expectation of EM algorithm:
  𝑄(𝜆,𝜆 ̂ )= ∑${}_I$ 𝑙𝑜𝑔𝑃(𝑌,𝐼|𝜆)𝑃(𝑌,𝐼|𝜆 ̂ )
• (3) *Maximization of EM algorithm:
  max 𝑄(𝜆,𝜆 ̂ )

use Lagrangian multiplier method and take the partial derivative of Lagrangian funcition。

Application

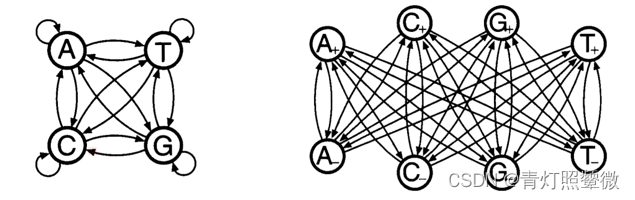
CpG island:

• In the human genome wherever the dinucleotide CG occurs, the C nucleotide is typically chemically modified by methylation.
• around the promoters or ‘start’ regions
• CpG is typically a few hundred to a few thousand bases long.
  
  three questions: of CpG island:
• Given the model of distinguished the CpG island, how to calculate the probability of the observation sequence ?
• Given a short stretch of genomic sequence, how would we decide if it comes from a CpG island or not ?
• Given a long piece of sequence, how would we find the CpG islands in it?
  

reference：

• Markov chain Defination
• A Revealing Introduction to Hidden Markov Models
  
• Top 10 Algorithms in Data Mining
• An Introduction to Hidden Markov Models for Biological Sequences
• python-hmmlearn-example
• Viterbi algorithm
• Baum-Welch blog
• Biological Sequence Analysis. Probabilistic Models of Proteins and Nucleic Acids. R. Durbin, S. Eddy, A. Krogh and G. Mitchison

---

未完待续…