【C++笔试强训】第二十四天

🎇C++笔试强训

---

• 博客主页：一起去看日落吗
• 分享博主的C++刷题日常，大家一起学习
• 博主的能力有限，出现错误希望大家不吝赐教
• 分享给大家一句我很喜欢的话：夜色难免微凉，前方必有曙光 🌞。

---

💦🔥

---

选择题

💦第一题

请指出选择排序，冒泡排序，快速排序的时间复杂度分别是（）

A O(n^2)、O(n2)、O(nlog2n)
B O(nlog2n)、、O(n^2)、O(nlog2n）
C O(n)、O(n^2)、O(n2)
D O(nlog2n)、O(n^2)、O(n2)

先进排序都是对数阶，一般排序方法都是n方

这道题的答案是A

---

💦第二题

在单链表中，增加头结点的目的是（）

A 标识表结点中首结点的位置
B 算法实现上的方便
C 使单链表至少有一个结点
D 说明单链表是线性表的链式存储实现

增加头节点代码会简单些，做其他节点的插入删除两个没区别，如果是第一个节点，不带头节点需要特殊处理

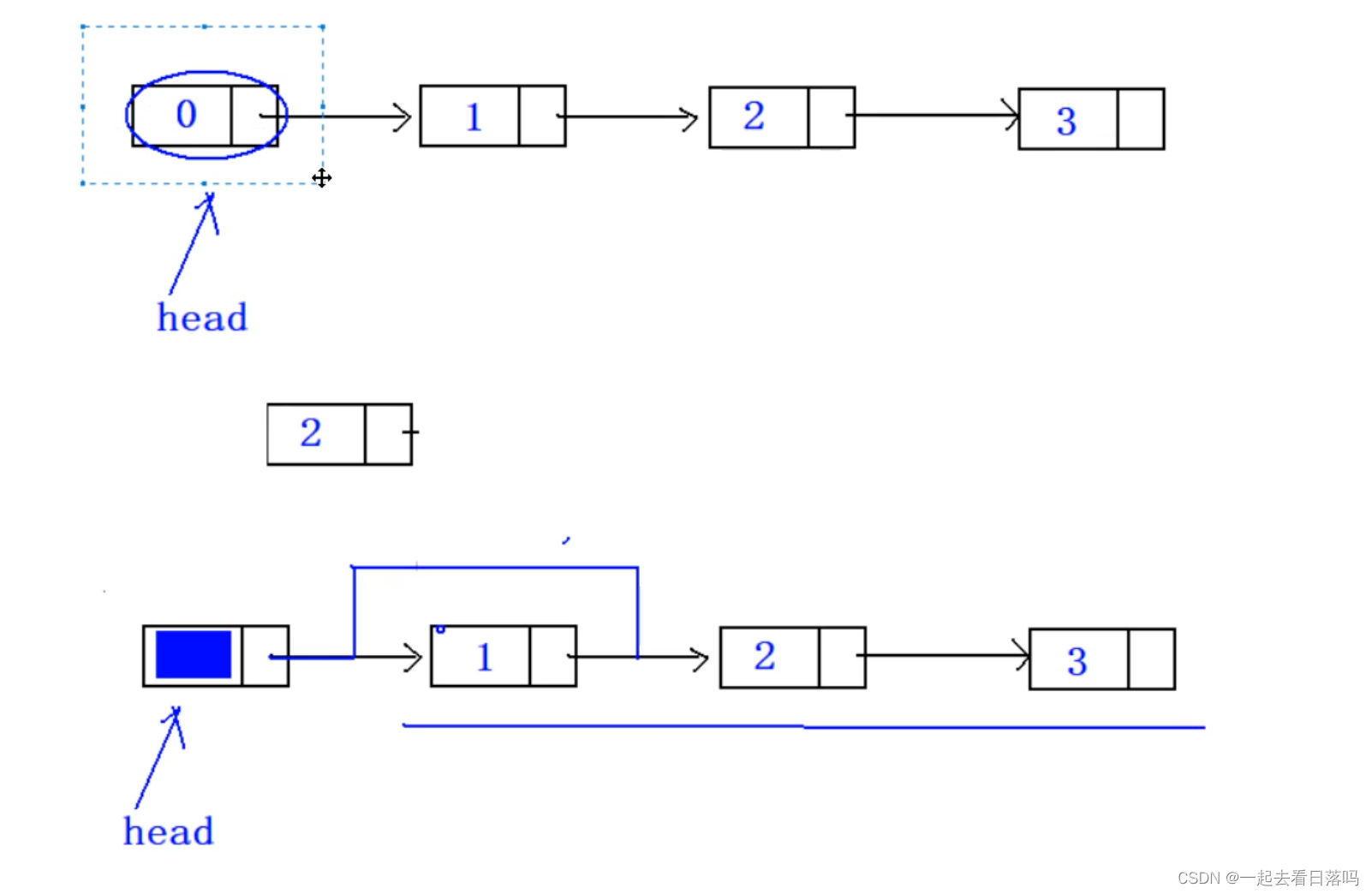
这道题的答案是B

---

💦第三题

下列算法的功能是什么？

/*L是无头节点单链表*/
LinkList Demo(LinkList L){
	ListNode *Q,*P;
	if(L&&L->next){
		Q=L;
		L=L->next;
		P=L;
		while(P->next)
			P=P->next;
		p->next=Q;
	}
	return L;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

根据代码的操作画图，得出结论是让链表变得循环了

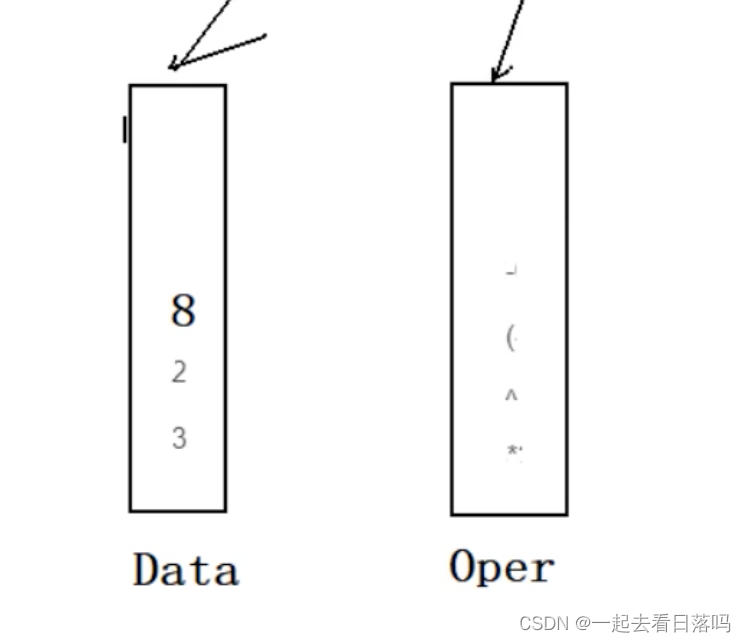
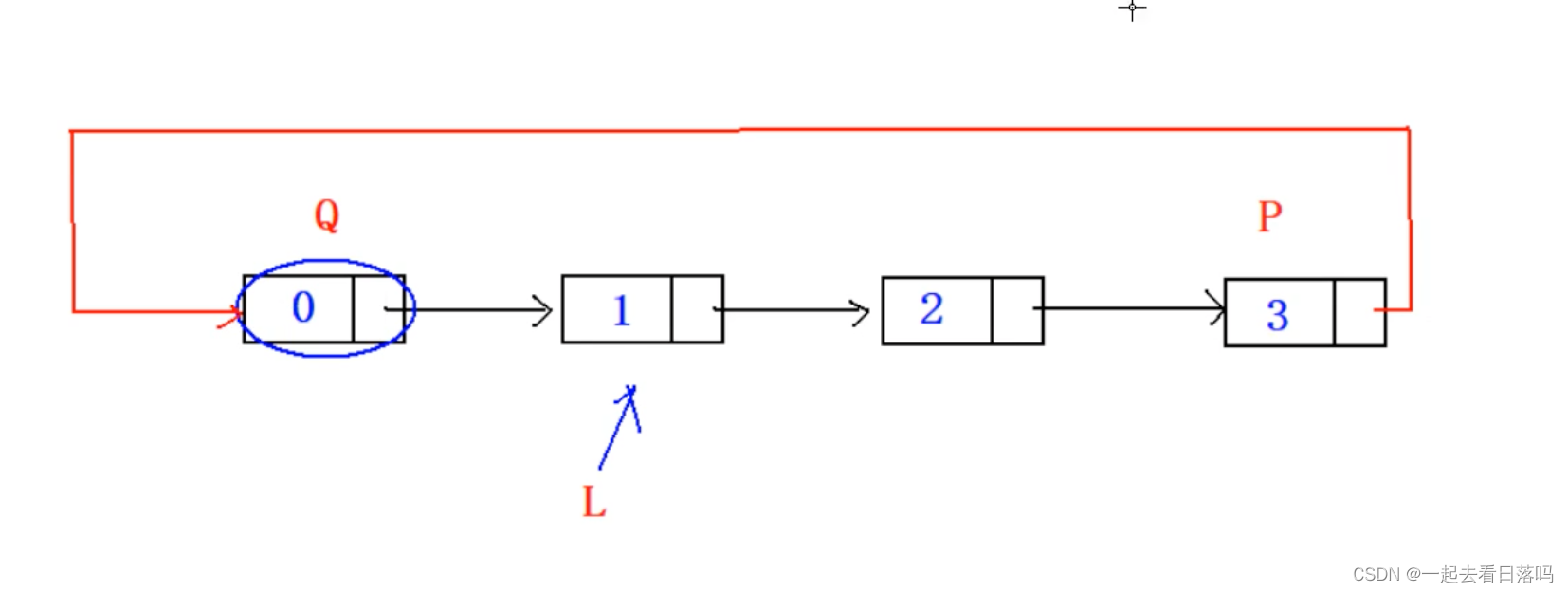
A 遍历链表

B 链表深拷贝

C 链表反转

D 单链表转变为循环链表

这道题的答案是D

---

💦第四题

表达式32^(4+22-6*3)-5求值过程中当扫描到6时,对象栈和运算符栈为(),其中 ^ 为乘幂

A 3,2,4,1,1;( * ^(+ * -
B 3,2,8;( * ^ -
C 3,2,4,2,2; ( * ^(-
D 3,2,8;*^(-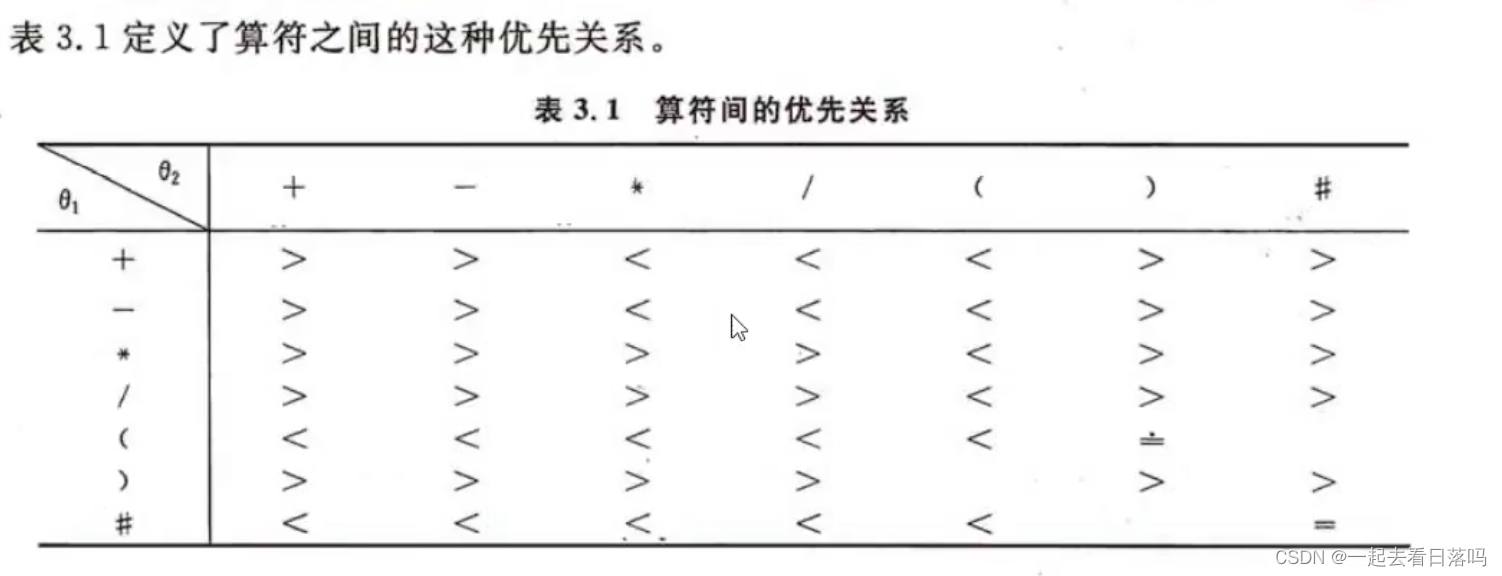

这道题的答案是D

---

💦第五题

假设以数组A[60]存放循环队列的元素,其头指针是front=47,当前队列有50个元素,则队列的尾指针值为()

A 3
B 37
C 97
D 50

这道题很简单，当前是47，存50个元素，就是47+50-60 = 37

这道题的答案是B

---

💦第六题

一棵完全二叉树第六层有9个叶结点（根为第一层），则结点个数最多有（）

A 112
B 111
C 107
D 109

第六层有九个结点，七层满二叉树的结点个数 2 ^ 7 - 1 = 128

则这棵树的结点 128 - 9 * 2 = 109

这道题主要考察二叉树的性质

这道题的答案是D

---

💦第七题

有权值分别为11，8，6，2，5的叶子结点生成一棵哈夫曼树，它的带权路径长度为（）

A 24
B 71
C 48
D 53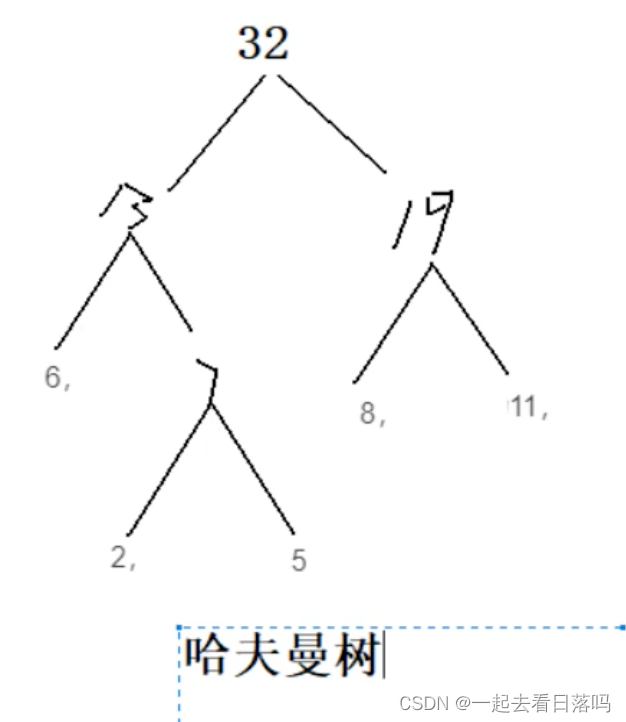

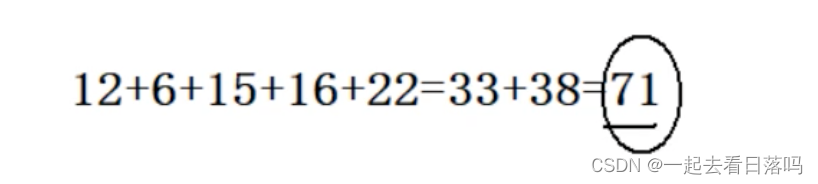
这道题的答案是B

---

💦第八题

已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，最后的叶子节点为（）

A 34

B 21

C 16

D 12

这道题的答案是C

---

💦第九题

将10个元素散列到100000个单元的哈希表中,则()产生冲突

A 一定会

B 一定不会

C 仍可能会

空间很多，数据很少，哈希最大的特点是空见少数据多，哈希函数是映射函数，保不准数据很特殊，可能还是会映射同一个地址，只不过是产生冲突的可能性减少了，不能保证一定不会产生冲突

这道题的答案是C

---

💦第十题

下列排序算法中，元素的移动次数与关键字的初始排列次序无关的是 （） 。

A 直接插入排序

B 起泡排序

C 基数排序

D 快速排序

ABD正序和反序都不同，基数排序是不需要移动数据和比较数据的，是所有排序里面唯一的，是通过分发和收集对数据的排序

这道题的答案是C

---

编程题

🔥 第一题

链接：年终奖

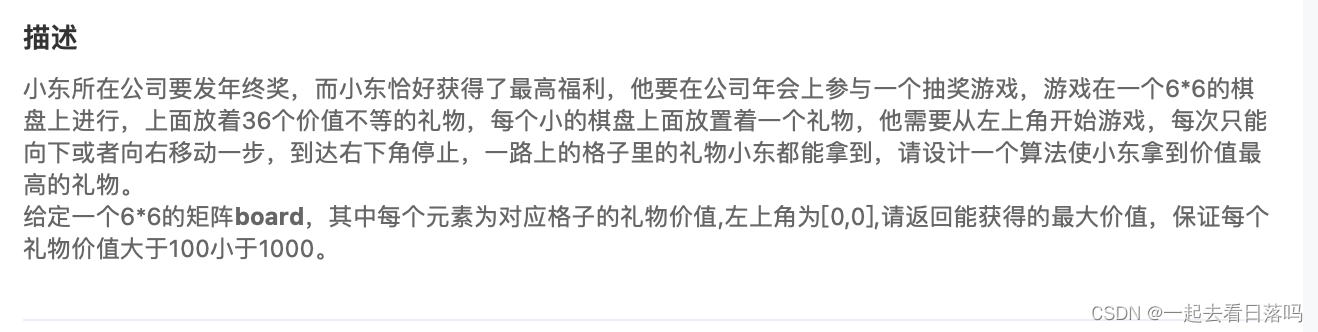
• 解题思路

本题需要使用动态规划求解。
定义f(i,j)表示从左上角走到坐标(i，j)处能获得的最大奖励。
搜索所有从左上角走到右下角的路径，找到最优路径。
f(i,j)分三种情况：
第一列：f(i, 0) = f(i-1, 0) + board(i, 0)
第一行：f(0,j) = f(0, j - 1) + b(0, j)
其它位置：f(i, j) = max{f(i-1, j), f(i, j - 1)} + board(i, j)
最后返回右下角的值。

• 代码演示

class Bonus {
public:
    int getMost(vector<vector<int> > board) {
        // write code here
        int row = board.size();
        int col = board[0]. size();

        vector<vector<int>> allPrice(row,vector<int> (col,0));

        allPrice[0][0] = board[0][0];

        for(int i = 0;i < row;++i)
        {
            for(int j = 0;j < col;++j)
            {
                if(i == 0 && j == 0)
                    continue;

                if(i == 0)//在第一行，只能往右走
                    allPrice[i][j] = allPrice[i][j-1] + board[i][j];
                else if(j == 0)//在第一列，只能往下走
                    allPrice[i][j] = allPrice[i-1][j] + board[i][j];
                else
                    allPrice[i][j] = max(allPrice[i][j-1],allPrice[i-1][j]) + board[i][j];
            }
        }
        return allPrice[row-1][col-1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

---

🔥 第二题

链接：迷宫问题

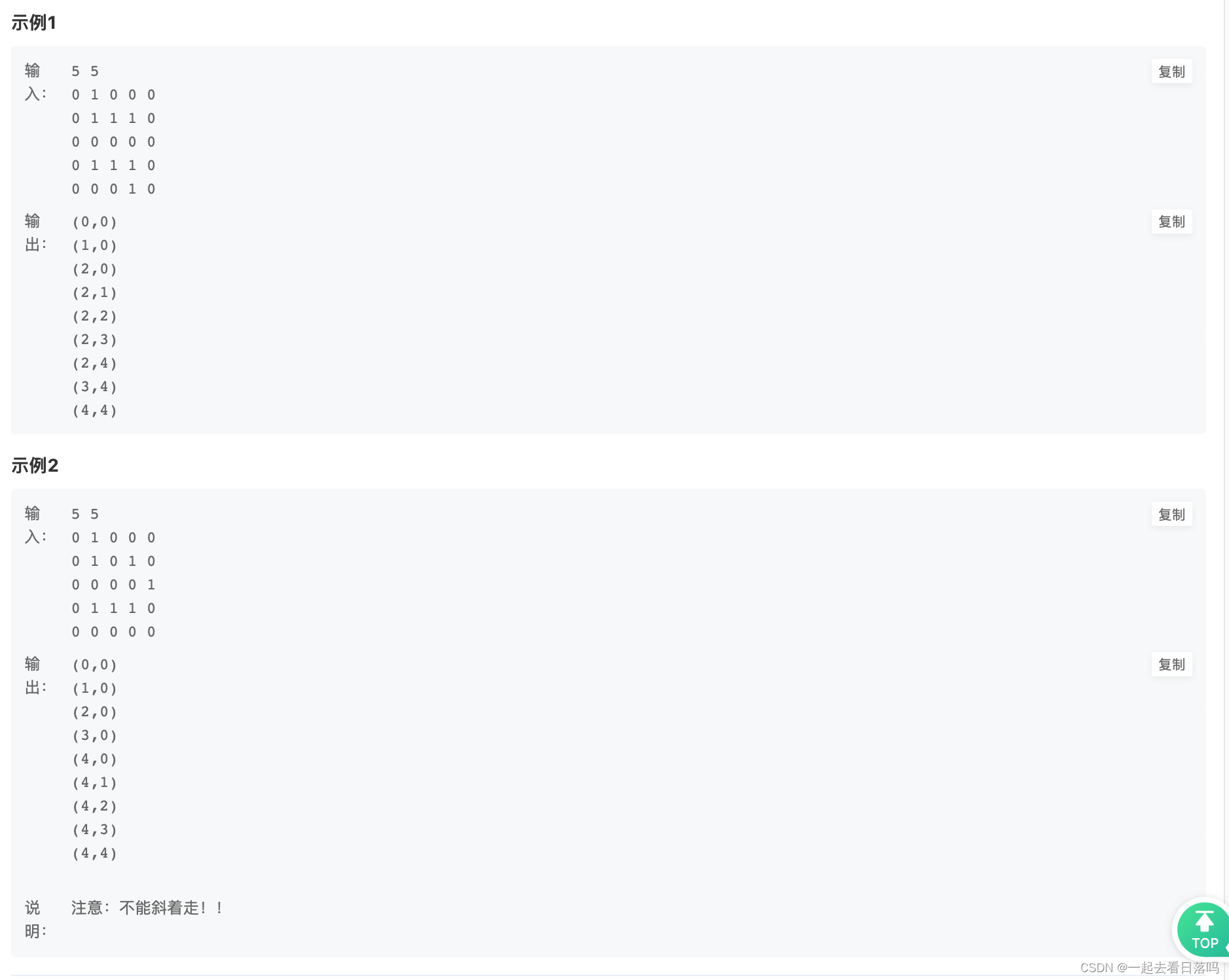
• 解题思路

本题可用回溯法求解 具体步骤为：

1. 首先将当前点加入路径，并设置为已走
2. 判断当前点是否为出口，是则输出路径，保存结果；跳转到4
3. 依次判断当前点的上、下、左、右四个点是否可走，如果可走则递归走该点
4. 当前点推出路径，设置为可走

• 代码演示

#include 
#include 
using namespace std;

int ROW,COL;
vector<vector<int>> maze;
vector<vector<int>> path_tmp;//临时路径
vector<vector<int>> path_best;//最佳路径

void MazeTrack(int i ,int j)
{
    maze[i][j] = 1;//代表（i，j）已经走过
    path_tmp.push_back({i,j});

    //判断是否到达出口
    if(i == ROW - 1 && j == COL - 1)
    {
        if(path_best.empty() || path_best.size() > path_tmp.size())
            path_best = path_tmp;
    }

    //向右走
    if(j+1 < COL && maze[i][j+1] == 0)
        MazeTrack(i, j+1);
    //向左走
    if(j-1 >= 0 && maze[i][j-1] == 0)
        MazeTrack(i, j-1);
    //向上走
    if(i-1 >= 0 && maze[i-1][j] == 0)
        MazeTrack(i-1,j);
    //向下走
    if(i+1 < ROW && maze[i+1][j] == 0)
        MazeTrack(i+1, j);

    maze[i][j] = 0;//回溯，恢复
    path_tmp.pop_back();
}

int main()
{
    while(cin >> ROW >> COL)
    {
        maze = vector<vector<int>>(ROW,vector<int>(COL,0));//开辟迷宫空间 
        path_tmp.clear();
        path_best.clear();
        //输入迷宫
        for(int i = 0;i < ROW;++i)
        {
            for(int j = 0;j < COL;++j)
            {
                cin >> maze[i][j];
            }
        }

        MazeTrack(0,0);//从（0，0）位置开始走

        //输出路径
        for(int i = 0;i < path_best.size();++i)
        {
            cout << "(" << path_best[i][0] << "," << path_best[i][1] << ")" << endl;
        }
    }
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

---