LCT 的基本操作

一 点睛

LCT 有 7 种基本操作

• access(x) 

• makeroot(x) 

• findroot(x)

• split(x , y)

• link(x , y)

• cut(x , y)

• isroot(x)

二 access(x)

1 定义

access(x) 是动态树所有操作的基础，用于打通 x 到原树根节点的一条实链。

2 图解

a 原树变化

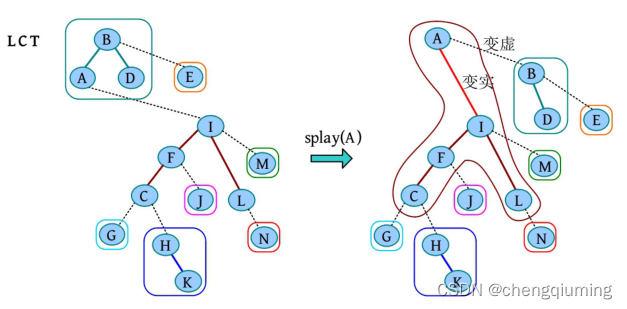
access(L) 指将 L 到树根的路径变为实链，这条实链上的节点 L、I、F、C、A 与其他子节点的边变虚边，原树的变化如下图所示。

b LCT 变化

（1）将 L 旋转为所在伸展树的根，将 L 的右儿子置空（相当于变虚边）。

（2）将 L 的父节点 I 也旋转到所在伸展树的根，将 I 的右儿子置为 L。

（3）将 I 的父节点 A 也旋转到所在伸展树的根，将 A 的右儿子置为 I。此时，A-C-F-I-L 是一条实链，由一棵伸展树维护（按节点在原树中的深度，中序有序），如下图所示。

三 makeroot(x)

1 定义 

将指定的点 x 换成原树的根。

2 换根操作

① access(x)，打通一条 x 到原树根的实链。

② splay(x)，将 x 旋转为所在伸展树的根。

③ reverse(x)，反转当前伸展树的左右子树。

3 图解

（1）access(L)，得到一条 L 到原树根的实链，此时 L 在该实链中深度最大。原树和 LCT 的变化如下图所示。

（2）splay(L)，将 L 旋转为所在伸展树的根，在原树中，L 是该实链上深度最大的节点，因此在当前伸展树中，L 没有右子树。

（3）reverse(L)。在原树中，树根的深度最小，于是反转当前伸展树的左右子树，使所有节点的深度都倒过来，原来按照深度递增形成的序列为 A-C-F-I-L，反转后按照深度递增形成的序列为 L-I-F-C-A。此时 L 没有左子树，反倒成了深度最小的点（根节点）。

四 findroot(x)

1 定义

findroot(x) 表示查找 x 所在原树的树根，主要用来判断两点之间的连通性。若 findroot(x) = findroot(y)，则表明x 、y 在同一棵树中。

2 操作步骤

① access(x)，打通一条 x 到原树根的实链。

② splay(x )，将 x 旋转为所在伸展树的根。

③ 查找当前伸展树的最左节点（深度最小的点，即树根），返回根节点即可。

3 图解 

原树及对应的 LCT 如下图所示，求 L 所在原树的树根 findroot(L)，操作过程如下。

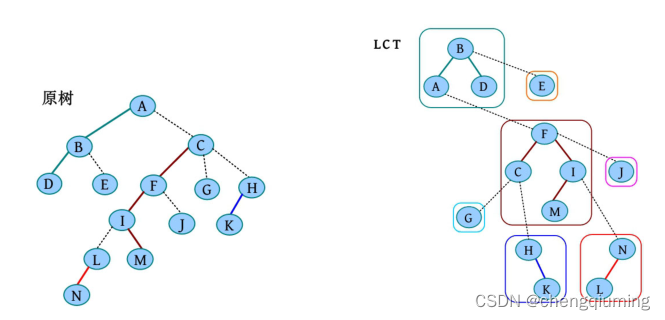
执行 access(L)、splay(L) 之后的 LCT 如下图所示。

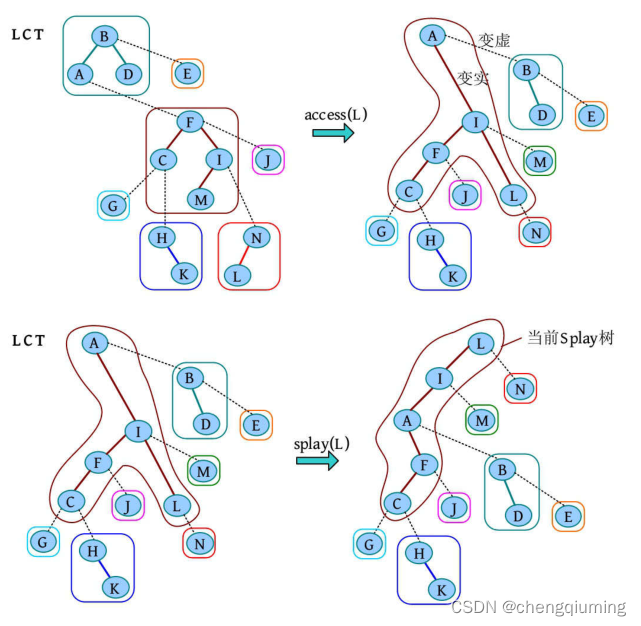
当前伸展树的最左节点为 A（深度最小的点，即树根），返回根节点 A 即可。

五 split(x , y)

1 定义

split(x , y) 表示分离出 x -y 的路径为一条实链，用一个伸展树维护。

2 分离步骤

① makeroot(x)，将 x 变成原树的根。

② access(y)，打通一条 y 到原树根的实链。

③ splay(y )，将 y 旋转到当前伸展树的树根。

3 图解

原树及其对应的 LCT 如下图所示，分离出 L-B 的路径，操作过程如下。

（1）makeroot(L)，将 L 变为原树的树根，对应的 LCT 如下图所示。

（2）access(B)，打通 B 到根的一条实链，这条实链的中序序列正好是原树中 L-B 的路径 L-I-F-C-A-B，对应的 LCT 如下图所示。

（3）splay(B)，将 B 旋转到当前伸展树的根，对应的 LCT 如下图所示。

六 link(x , y)

1 定义

link(x , y) 表示在 x 、y 之间连接一条边。若 x 、y 之间连通，则不可以连边。

2 操作步骤

① makeroot(x) 将 x 变成原树的根。

② 将 x 的父节点修改为 y，fa(x)=y。

3 图解

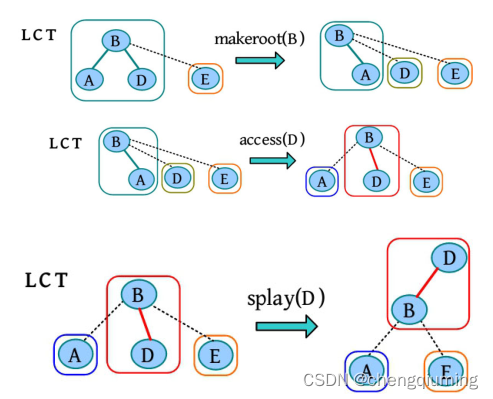
例如，两棵原树和对应的 LCT 如下图所示，在 B、H 之间连接一条边，操作过程如下。

（1）makeroot(B)，将 B 变为原树的树根，对应的 LCT 如下图所示。

（2）fa[B]=H，将 B 的父节点修改为 H，相当于在 LCT 中连接了 B-H 的一条虚边，对应的 LCT 如下图所示。

七 cut(x , y)

1 定义

cut(x , y) 表示将 x -y 的边断开（删边）。若 x、y 之间不连通，则不可以删边。若 x、y 之间连通，则还要判断两者之间是否有边，因为连通只代表有一条通路，中间可能有节点。

2 操作步骤

① split(x , y)，分离出 x-y 的路径为一条实链，若 x 不是 y 的左儿子或 x 有右子树，则说明 x 到 y 之间有其他节点，不能删边。

② 将 x-y 的边断开，修改 y 的左儿子为 0，y 的左儿子的父节点为 0。

③ update(y)，更新 y 的相关信息。

3 图解

原树及对应的 LCT 如下图所示，将 B-D 的边断开，操作过程如下。

（1）split(B, D) 分 3 步

① makeroot(B) 

② access(D)

③ splay(D)

（2）双向断开 B-D 的连接。

八 isroot(x)

isroot(x) 表示判断 x 是否为所在伸展树的根。注意：伸展树的根和原树的根不是一回事。若 x 是所在伸展树的根，则 x 与其父节点之间是一条虚边，x 既不是其父节点的左儿子，也不是其父节点的右儿子。例如，原树及对应的 LCT 如下图所示，N 是其所在伸展树的树根，既不是其父节点I的左儿子，也不是右儿子；F 是其所在伸展树的树根，既不是其父节点 A 的左儿子，也不是右儿子。A 没有左右儿子，A 和 F 之间的虚边仅说明 F 的父节点是 A，A 却不把 F 当作儿子，即“认父不认子”。