图形学-几何-网格操作

1. 什么是网格操作?

我们会对模型的网格进行一些操作来达到我们使用的目的。基本的操作包括网格细分（Mesh Subdivision），网格简化（Mesh Simplify）以及网格正则化（Mesh Regularization）。本章将会对前两个操作进行讲解。网格正则化指的是将三角形的平面变成接近于正三角形的一种操作。

2. 网格细分

网格细分（Mesh Subdivision）会增加更多的三角形面数量，可以看到更多的细节。细分分为两步，第
一步是增加三角形的数量，第二步是计算三角形的位置（实际就是计算顶点位置）。

3. Loop 细分

Loop 细分适用于只有三角形面的模型。首先，每一个三角形面上我们依次连接三条边中点划分为四个
新的三角形面。每条边上的中点称为新顶点（New Vertex），原来三角形面上的三个顶点称为旧顶点（OldVertex）。

对于新顶点和旧顶点，我们采用不同的位置计算方法：

对于非边界上的新顶点，一定被两个三角形面共享。我们假设共享边的顶点是 𝐴, 𝐵，非共享边的两个顶
点是 𝐶, 𝐷，那么新顶点的位置是：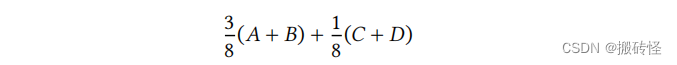

对于旧顶点，假设顶点的度为 𝑛，原顶点为 𝑂，周围顶点位置之和为 𝑆，那么新的顶点位置是：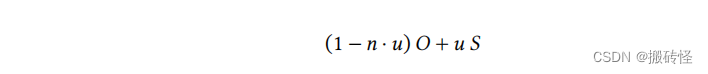

这里，𝑢 = 3/8n
顶点的计算是一个加权平均的过程，会使整个模型更加的平滑。

4. Catmull-Clark 细分

Catmull-Clark 细分适用于某些面是非三角形的时候进行细分。我们做出以下定义，如果一个面是四边形，那么称为四边形面，反之为非四边形面。任何一个度不是 4 的点都称为奇异点，反之为非奇异点。

每一次细分我们都在每一条边的中点产生新的顶点，并在每一个面上引入一个中点，将面的中点和边上的中点相连，这就是一次细分操作。这样的细分操作满足一下规律：

1. 在第一次细分后，所有原本是非四边形内部都会引入奇异点，并且所有的面都变成了四边形面；
2. 之后的细分，不会再引入新的奇异点，所有的面都是四边形面。

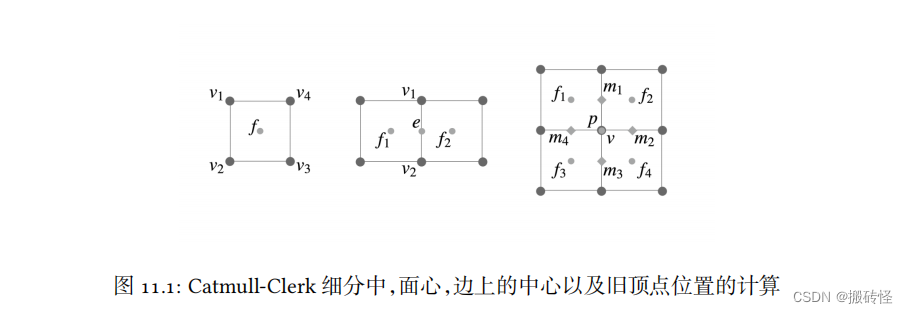
这样，对于出现各种形状的面，我们都可以进行细分。这些点新的位置的计算方式如下：对于面心的点𝑓 ，计算方式为：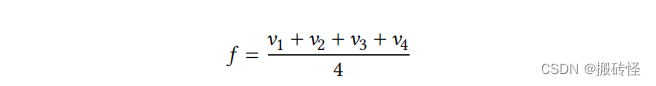

对于边上新生成的中点 𝑒，计算公式为:

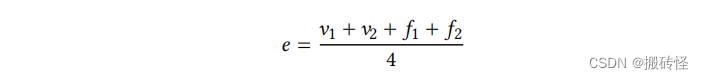
对于旧顶点 𝑣，新的位置的计算公式为：

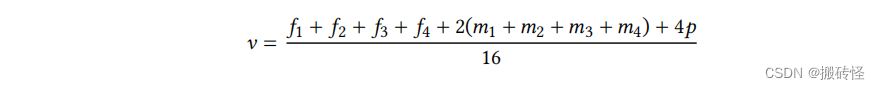
5. 网格简化

网格简化（Mesh Simplify）通过减少模型的面数简化模型。对于一个模型，我们可以通过构造不同的层级，在不同的情况下选择不同的模型。

我们使用坍缩（Collapsing）的方式进行网格简化。我们将边坍缩变成一个点。我们希望这个点和旧顶点连接后与之前的形状差不多，因此我们引入二次误差度量（Quadric Error Metrics）来度量任意一点与旧顶点连接后与原来的相似程度，并选择最小值作为结果.

在模型中，当我们进行坍缩的时候，我们会对所有可以坍缩的点进行排序，每一次探索误差最小的点后，更新这个点周围的点新的误差值。这里采用堆进行实现。

网格简化是一种贪心算法，我们使用局部的最优解并认为是全局最优的结果