七天强化学习DAY1-2｜(二)马尔科夫决策过程MDP｜学习笔记

这一篇主要就是讲如何利用马尔科夫决策过程(Markov Decision Process)简化强化学习模型；MDP这一篇对应Sutton书的第三章和UCL强化学习课程的第二讲。

强化学习（二）马尔科夫决策过程(MDP) - 刘建平Pinard - 博客园

目录

1.强化学习引入MDP的原因

2.MDP的价值函数与贝尔曼方程

3. 状态价值函数与动作价值函数的递推关系

4.最优价值函数

5.MDP实例(本节难点)

6.MDP小结　 ​​​​​​​

---

1.强化学习引入MDP的原因

        强化学习的8个要素我们在第一节已经讲了。其中的第七个是环境的状态转化模型，它可以表示为一个概率模型，即在状态s下采取动作a，转到下一个状态s'的概率，表示为

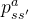
        如果按照真实的环境转化过程看，转化到下一个状态s'的概率既与上一个状态s有关，还与上上个状态，以及上上上个状态有关。这会使环境转化模型非常复杂，复杂到难以建模。因此我们需要对其进行简化。简化的方法就是假设状态转化的马尔科夫性，也就是假转化到下一个状态s'的概率仅与上一个状态s有关，与之前的状态无关。用公式表示就是：

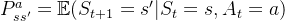
        对于马尔科夫性本身，本身是一个比较简单的假设：(1)齐次马尔科夫链假设。即任意时刻的隐藏状态只依赖于它前一个隐藏状态；(2) 观测独立性假设。即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态，这也是一个为了简化模型的假设。

        第四个要素：个体策略(policy)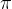也做了马尔科夫假设，即在状态s时采取动作a的概率仅与当前状态s有关，与其他要素无关，用公式表示就是：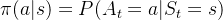

        第五个要素：价值函数 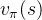也是一样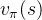，现在仅仅依赖于当前状态，价值函数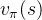 

表示为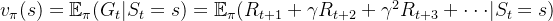：，其中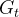 代表收获(return)，是一个MDP中从某一状态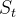开始采样直到终止状态时所有奖励的有衰减的之和。

2.MDP的价值函数与贝尔曼方程

        对于MDP，我们在第一节里已经讲到了它的价值函数表达式，但是这个表达式没有考虑到所采用的动作a带来的价值影响，因此我们除了状态价值函数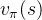外，还有一个动作价值函数 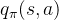，即：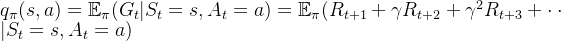

        根据价值函数的表达式，我们可以推导出价值函数基于状态的递推关系，比如对于状态价值函数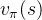，得到：

3. 状态价值函数与动作价值函数的递推关系

        根据动作价值函数 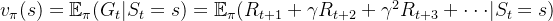和状态价值函数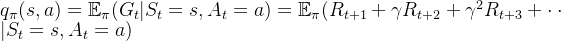  

的定义，我们很容易得到它们之间的转化关系公式： 

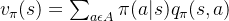
        也就是说，状态价值函数是所有动作价值函数基于策略𝜋的期望。通俗说就是某状态下所有状态动作价值乘以该动作出现的概率，最后求和，就得到了对应的状态价值。

        反过来，利用贝尔曼方程，我们也很容易通过状态价值函数表示动作价值函数，即：

---

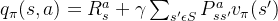
        通俗说就是状态动作价值由两部分相加组成，第一部分是即时奖励，第二部分是环境所有可能出现的下一个状态的概率乘以该下一状态的状态价值，最后求和，并加上衰减。

        这两个转化过程也可以从下图中直观的看出：

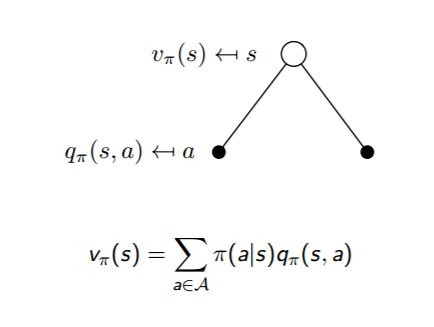
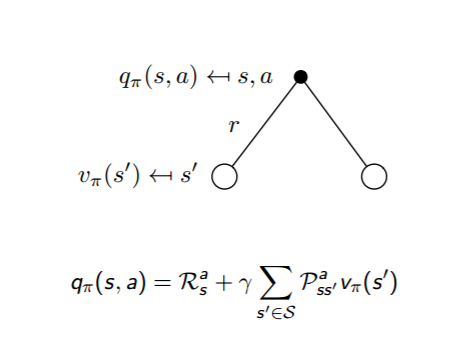
        把上面两个式子互相结合起来，我们可以得到：

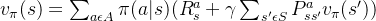
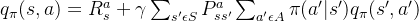
4.最优价值函数

        解决强化学习问题意味着要寻找一个最优的策略让个体在与环境交互过程中获得始终比其它策略都要多的收获，这个最优策略我们可以用 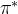 表示。一旦找到这个最优策略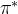，那么我们就解决了这个强化学习问题。一般来说，比较难去找到一个最优策略，但是可以通过比较若干不同策略的优劣来确定一个较好的策略，也就是局部最优解。

        如何比较策略的优劣呢？一般是通过对应的价值函数来比较的，也就是说，寻找较优策略可以通过寻找较优的价值函数来完成。可以定义最优状态价值函数是所有策略下产生的众多状态价值函数中的最大者，即：

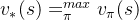
        同理也可以定义最优动作价值函数是所有策略下产生的众多动作状态价值函数中的最大者，即：

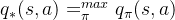
        对于最优的策略，基于动作价值函数我们可以定义为：

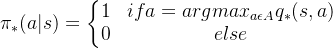
        同时，利用状态价值函数和动作价值函数之间的关系，我们也可以得到:

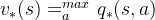
        最优价值函数关系也很容易得到：

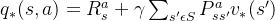
        利用上面的两个式子也可以得到和第三节末尾类似的式子：

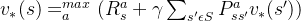
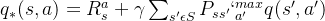
‼️上述设计公式很多，需要花费时间慢慢消化‼️

5.MDP实例(本节难点)

        如何利用给定策略来计算价值函数：

 

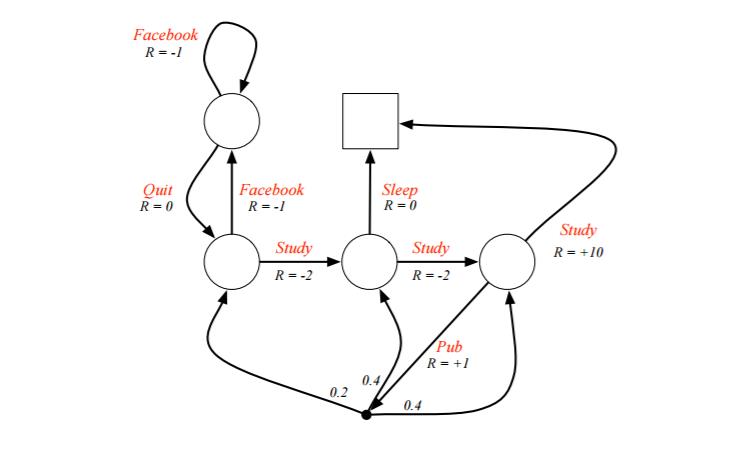
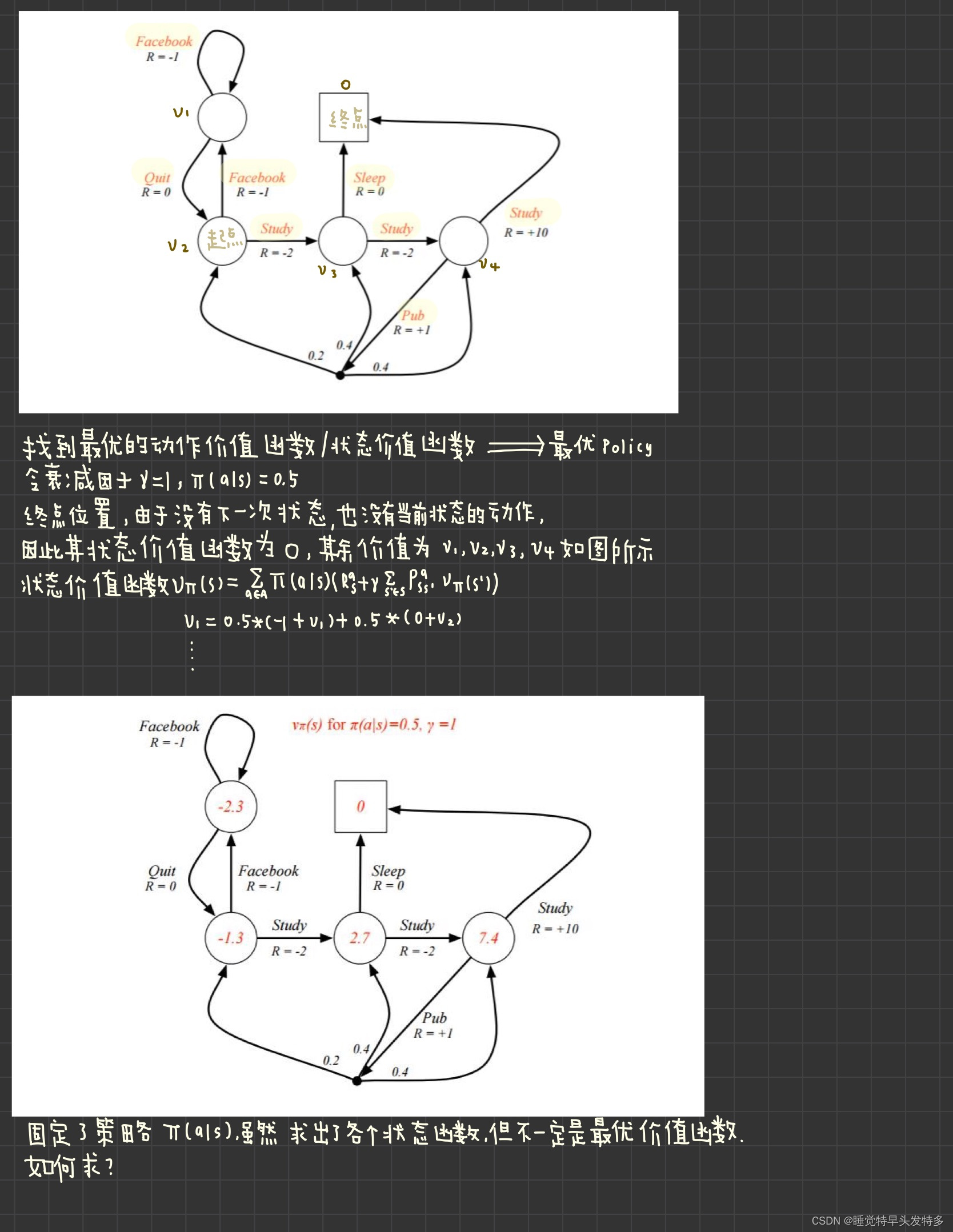
        终点处好求，以动作价值函数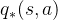为例求解：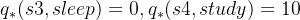

        接着利用 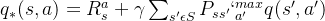 列方程组求出所有的 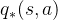，再利用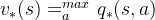求出所有的。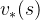

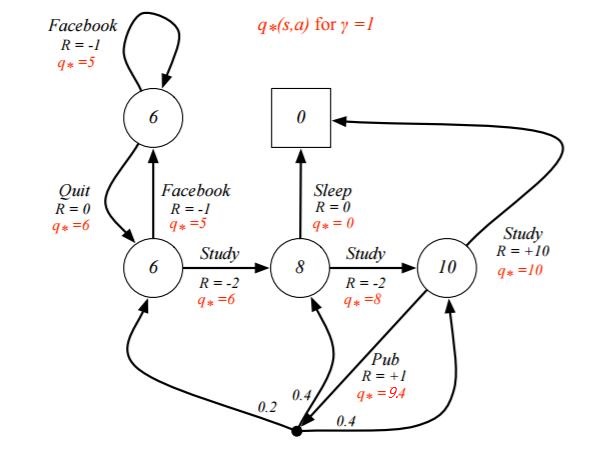
        从而我们的最优决策路径是走6->6->8->10->结束。　

6.MDP小结　 

        虽然MDP可以直接用方程组来直接求解简单的问题，但是更复杂的问题却没有办法求解，因此我们还需要寻找其他有效的求解强化学习的方法。