【LeetCode-中等】198. 打家劫舍（详解）

题目

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/house-robber

 

---

启初我想的太简单了，不就是两种么，每隔一个挑一个房间么，提交之后发现不然，因为有的时候为了最大的利润，是可以跳两个房间的。

 方法1：动态规划

思路、图片来源下面作者

作者：nettee
链接：https://leetcode.cn/problems/house-robber/solution/dong-tai-gui-hua-jie-ti-si-bu-zou-xiang-jie-cjavap/
来源：力扣（LeetCode）

这道题是典型的动态规划题，动态规划问题主要有下面三个步骤

• 定义子问题
• 写出子问题的递推关系
• 确定 DP 数组的计算顺序

步骤一：定义子问题
稍微接触过一点动态规划的朋友都知道动态规划有一个“子问题”的定义。什么是子问题？子问题是和原问题相似，但规模较小的问题。例如这道小偷问题，原问题是“从全部房子中能偷到的最大金额”，将问题的规模缩小，子问题就是“从 kk 个房子中能偷到的最大金额”，用 f(k)f(k) 表示。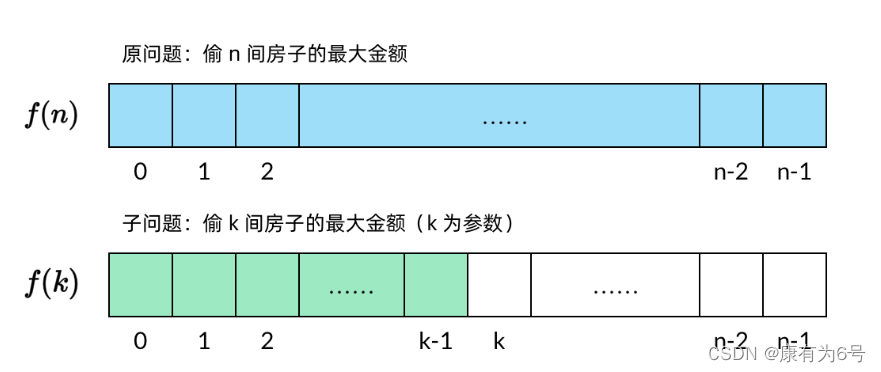

可以看到，子问题是参数化的，我们定义的子问题中有参数 kk。假设一共有 nn 个房子的话，就一共有 nn 个子问题。动态规划实际上就是通过求这一堆子问题的解，来求出原问题的解。这要求子问题需要具备两个性质：

• 原问题要能由子问题表示。例如这道小偷问题中，k=nk=n 时实际上就是原问题。否则，解了半天子问题还是解不出原问题，那子问题岂不是白解了。
• 一个子问题的解要能通过其他子问题的解求出。例如这道小偷问题中，f(k)f(k) 可以由 f(k-1)f(k−1) 和 f(k-2)f(k−2) 求出，具体原理后面会解释。这个性质就是教科书中所说的“最优子结构”。如果定义不出这样的子问题，那么这道题实际上没法用动态规划解。

小偷问题由于比较简单，定义子问题实际上是很直观的。一些比较难的动态规划题目可能需要一些定义子问题的技巧。

步骤二：写出子问题的递推关系

 

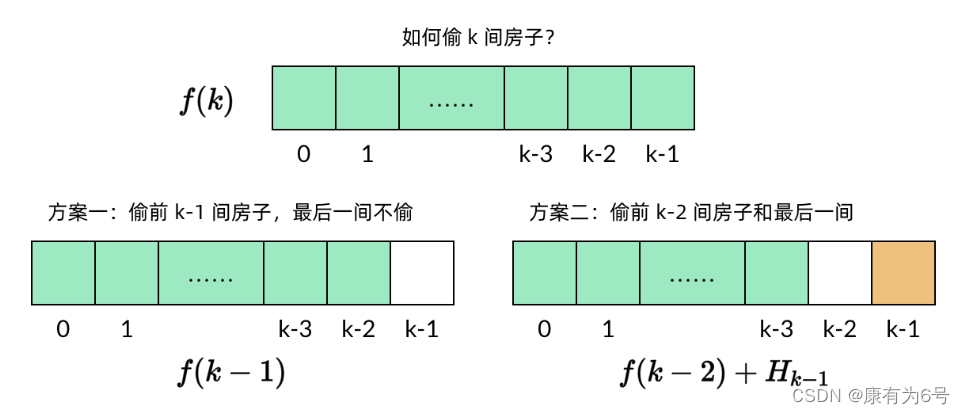
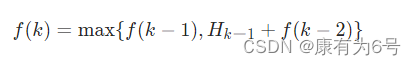
在写递推关系的时候，要注意写上 k=0k=0 和 k=1k=1 的基本情况：

当 k=0 时，没有房子，所以 f(0)=0
当 k=1 时，只有一个房子，偷这个房子即可，所以 f(1) = H0

步骤三：确定 DP 数组的计算顺序
大部分动态规划问题都是自底向上的。

DP 数组也可以叫”子问题数组”，因为 DP 数组中的每一个元素都对应一个子问题。如下图所示，dp[k] 对应子问题 f(k)，即偷前 k间房子的最大金额。

 

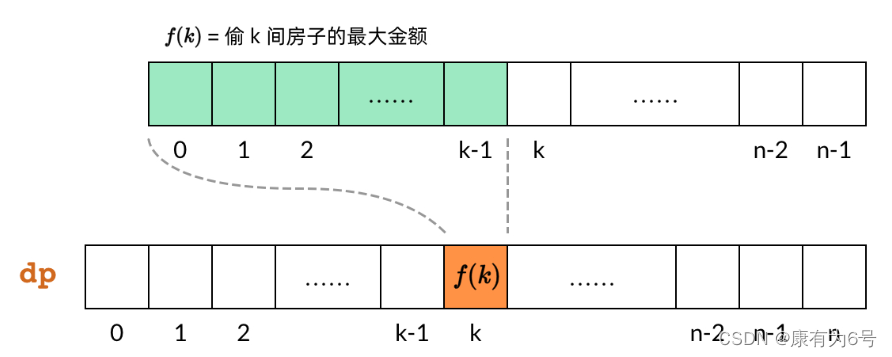
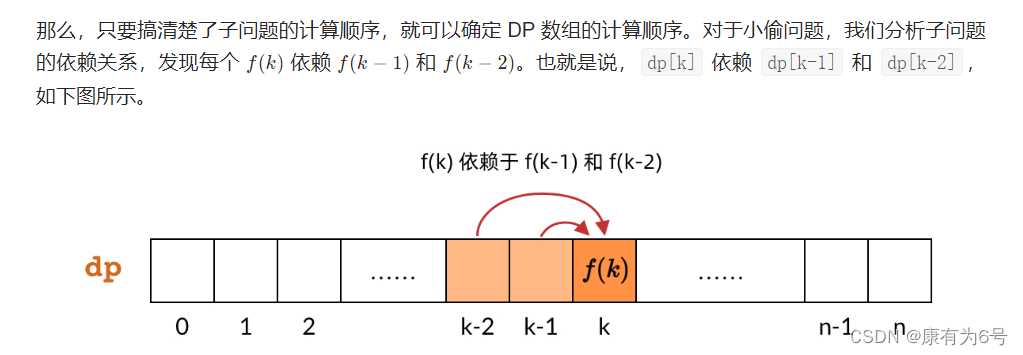
那么，既然 DP 数组中的依赖关系都是向右指的，DP 数组的计算顺序就是从左向右。这样我们可以保证，计算一个子问题的时候，它所依赖的那些子问题已经计算出来了。

确定了 DP 数组的计算顺序之后，我们就可以写出题解代码了：

public int rob(int[] nums) {
    if (nums.length == 0) {
        return 0;
    }
    int N = nums.length;
    int[] dp = new int[N+1];//最终结果就是dp数组最后一个
    dp[0] = 0;
    dp[1] = nums[0];
    for (int k = 2; k <= N; k++) {
        dp[k] = Math.max(dp[k-1], nums[k-1] + dp[k-2]);
    }
    return dp[N];
}
 

 

 动态规划真的强，最重要的是能写出递推公式，可以专门练习一下动态规划问题