0094 动态规划算法，KMP算法

 

 

 

 

 

 

 

/*
 * 动态规划算法
 * 1.将大问题划分为小问题进行解决，从而一步步获得最优解
 * 2.与分治法不同的是，它适用于动态规划求解问题，分解得到的子问题不是互相独立的
 * 3.动态规划可以通过 填表 的方式来逐步推进，得到最优解
 * 
 * 应用——背包问题
 * 一个给定容量的背包，若干具有一定价值和重量的物品，如何选择物品放入背包使背包物品价值最大
 * 其中又分01背包和完全背包（01背包指每个物品最多放1个，完全背包指每种物品都有无限件使用）
 * 
 * 思路
 * 设给定n个物品，设w[i]和v[i]分别为第i个物品的重量和价值，C为背包容量
 * 令v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值
 * 每次遍历得到的第i个物品，根据w[i]和v[i]来确定是否需要将该物品放入背包中：
 * 
 * 1.v[i][0] = v[0][j] = 0 //表示填入表第一行和第一列为0
 * 2.当 w[i]>j 时： v[i][j] = v[i-1][j] //当准备加入物品容量 大于 当前背包容量时，直接使用上一个单元格的装入策略
 * 3.当 w[i]<=j 时：v[i][j] = max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
 *      //当准备加入物品容量 小于等于 当前背包容量时，两种策略取最大值
 *          v[i-1][j]：上一个单元格装入的最大值
 *         v[i]：当前商品的价值
 *         v[i-1][j-w[i]]：装i-1个物品到剩余空间j-w[i]的最大值
 * 
 */
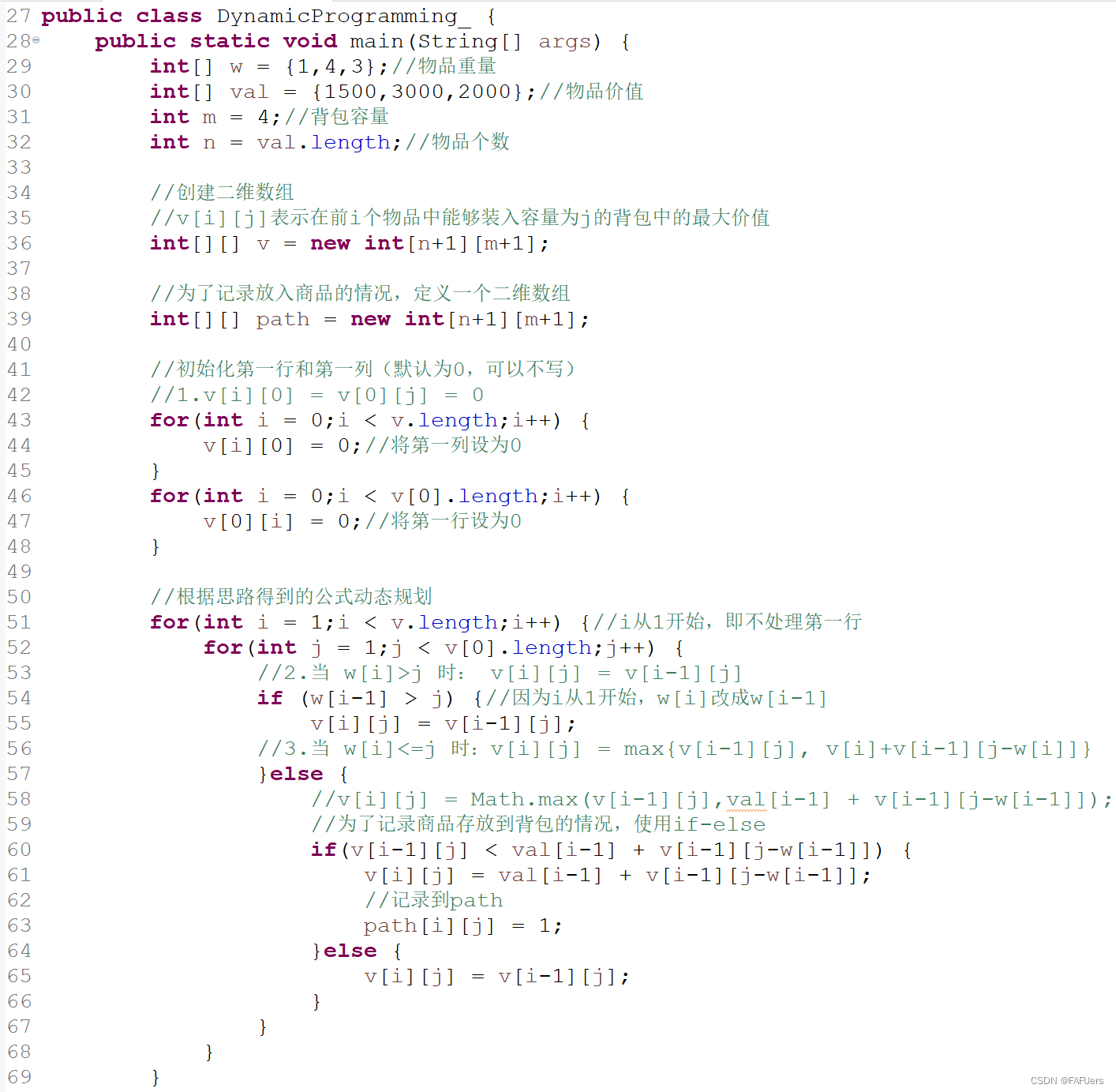
public class DynamicProgramming_ {
    public static void main(String[] args) {
        int[] w = {1,4,3};//物品重量
        int[] val = {1500,3000,2000};//物品价值
        int m = 4;//背包容量
        int n = val.length;//物品个数
        
        //创建二维数组
        //v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值
        int[][] v = new int[n+1][m+1];
        
        //为了记录放入商品的情况，定义一个二维数组
        int[][] path = new int[n+1][m+1];
        
        //初始化第一行和第一列（默认为0，可以不写）
        //1.v[i][0] = v[0][j] = 0
        for(int i = 0;i < v.length;i++) {
            v[i][0] = 0;//将第一列设为0
        }
        for(int i = 0;i < v[0].length;i++) {
            v[0][i] = 0;//将第一行设为0
        }
        
        //根据思路得到的公式动态规划
        for(int i = 1;i < v.length;i++) {//i从1开始，即不处理第一行
            for(int j = 1;j < v[0].length;j++) {
                //2.当 w[i]>j 时： v[i][j] = v[i-1][j]
                if (w[i-1] > j) {//因为i从1开始，w[i]改成w[i-1]
                    v[i][j] = v[i-1][j];
                //3.当 w[i]<=j 时：v[i][j] = max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
                }else {
                    //v[i][j] = Math.max(v[i-1][j],val[i-1] + v[i-1][j-w[i-1]]);
                    //为了记录商品存放到背包的情况，使用if-else
                    if(v[i-1][j] < val[i-1] + v[i-1][j-w[i-1]]) {
                        v[i][j] = val[i-1] + v[i-1][j-w[i-1]];
                        //记录到path
                        path[i][j] = 1;
                    }else {
                        v[i][j] = v[i-1][j];
                    }
                }
            }
        }
        
        //输出v
        for(int i = 0;i < v.length;i++) {
            for(int j = 0;j < v[0].length;j++) {
                System.out.print(v[i][j] + " ");
            }
            System.out.println();
        }
        
        System.out.println("==========最优解==============");
        //输出最后放入的是哪些商品
        int i = path.length - 1;//行的最大下标
        int j = path[0].length - 1;//列的最大下标
        while(i > 0 && j > 0) {//从path的最后开始找
            if (path[i][j] == 1) {
                System.out.printf("第%d个商品放入背包\n",i);
                j -= w[i-1];
            }
            i--;
        }
    }
}

import java.util.Arrays;

/*
 * 暴力匹配算法——字符串匹配问题
 * 1.如果当前字符匹配成功（str1[i]==str2[j]）,则i++,j++，继续匹配下一个字符
 * 2.如果匹配失败，令i=i-(j-1),j=0，相当于每次匹配失败，i回溯，j被置为0
 * 3.用暴力解决有大量回溯，每次只移动一位，若不匹配则移动到下一位，浪费了大量时间
 * 
 * KMP算法
 * 1.字符串查找算法，简称KMP算法，常用于在一个文本串S内查找一个模式串P的出现位置
 * 2.KMP算法利用之前判断过的信息，通过一个next数组，保存模式串中前后最长公共子序列的长度
 *   每次回溯时，通过next数组找到前面匹配过的位置，省去大量时间
 * 
 * 字符串"bread"
 * 前缀：b,br,bre,brea
 * 后缀：read,ead,ad,d
 * 部分匹配值：前缀和后缀的最长的共有元素长度
 * 移动位数 = 已匹配的字符数 - 对应的部分匹配值
 * 
 * KMP算法思想
 * 1.得到子串的部分匹配值表
 * 2.使用部分匹配表完成KMP匹配
 */
public class KMP_ {
    public static void main(String[] args) {
        String str1 = "BBC ABCDAB ABCDABCDABDE";
        String str2 = "ABCDABD";
        
        //暴力匹配算法
        int index = violenceMatch(str1, str2);
        System.out.println("index=" + index);
        
        //KMP算法
        //得到子串的部分匹配值表
        int[] next = kmpNext(str2);
        System.out.println("next=" + Arrays.toString(next));
        
        int index2 = kmpSearch(str1, str2, next);
        System.out.println("index2=" + index2);
    }
    
    //暴力匹配算法实现
    public static int violenceMatch(String str1,String str2) {
        char[] s1 = str1.toCharArray();
        char[] s2 = str2.toCharArray();
        int s1Len = s1.length;
        int s2Len = s2.length;
        
        int i = 0;//i指向str1
        int j = 0;//j指向str2
        while(i < s1Len && j < s2Len) {
            if (s1[i] == s2[j]) {
                i++;
                j++;
            }else {
                i = i - (j-1);
                j = 0;
            }
        }
        
        //判断是否匹配成功
        if (j == s2Len) {
            return i - j;
        }else {
            return -1;
        }
    }
    
    //KMP算法实现
    //获取到子串的部分匹配表
    public static int[] kmpNext(String dest) {
        //创建一个next数组保存部分匹配值
        int[] next = new int[dest.length()];
        //如果字符串长度为1，部分匹配值为0
        next[0] = 0;
        for(int i = 1,j = 0;i < dest.length();i++) {
            //当dest.charAt(i) != dest.charAt(j)时,需要从next[j-1]获取新的j
            //直到dest.charAt(i) == dest.charAt(j)成立后退出
            while(j > 0 && dest.charAt(i) != dest.charAt(j)) {
                j = next[j-1];
            }
            
            //当dest.charAt(i) == dest.charAt(j)时，部分匹配值+1
            if (dest.charAt(i) == dest.charAt(j)) {
                j++;
            }
            next[i] = j;
        }
        return next;
    }
    
    //KMP搜索算法
    //str1:原字符串，str2:子串，next:子串对应的部分匹配表
    public static int kmpSearch(String str1,String str2,int[] next) {
        //遍历str1
        for(int i = 0,j = 0;i < str1.length();i++) {
            //处理str1.charAt(i) ！= str2.charAt(j)
            while(j > 0 && str1.charAt(i) != str2.charAt(j)) {
                j = next[j - 1];
            }
            
            if(str1.charAt(i) == str2.charAt(j)) {
                j++;
            }
            
            if (j == str2.length()) {//找到
                return i - j + 1;
            }
        }
        return -1;
    }
}