2022年认证杯SPSSPRO杯数学建模C题(第一阶段)污水流行病学原理在新冠疫情防控方面的作用求解全过程文档及程序

2022年认证杯SPSSPRO杯数学建模

C题 污水流行病学原理在新冠疫情防控方面的作用

原题再现：

  2019 年新型冠状病毒肺炎疫情暴发至今已过两年，新型冠状病毒历经多次变异，目前已有 11 种变异毒株，包括阿尔法、贝塔、德尔塔、奥密克戎等。其中变异株奥密克戎已在世界上多个国家和地区流行。相比此前流行的变异株，奥密克戎具有大量关键突变，其传播力和隐匿性更强，且存在免疫逃逸，更容易多点散发或集中暴发。截至 2021-12-08，全球共有 57 个国家和地区报告奥密克戎变异株，截至 2022-01-20，奥密克戎已经波及我国 14 个省。虽然可以通过区域全员核酸检测的方式快速发现感染者并进行有效隔离。但是大规模核酸检测成本较高，而且对于经济、生活都会产生较大的影响，使用频率有限。为了解决这个问题，2020 年 8 月，世界卫生组织（WHO）发布了名为“新冠病毒环境监测的现状（Status of environmental surveillance forSARS-CoV-2 virus）”的科学简报。文中总结了通过市政污水进行新冠病毒监测的背景、方法和用途，为全球抗击疫情提供了一份指导方案。污水监测是以污水流行病学（Wastewater-Based Epidemiology，WBE）的原理为手段，通过分析市政污水处理厂进水中的污染物或者生物标记物浓度，结合人体代谢机理、进水流量和服务人群数量等信息，反推该物质在污水集水区内的状况，这一方法或在未来新冠疫情的大规模防控上发挥重要的作用。
  所谓污水流行病学便是基于污水中蕴藏的丰富信息，通过分析污水处理厂进水中的化学物质浓度，根据人体代谢机理、进水流量和服务人口数量估算该地区人群消费某类化学物质的规律，调查与之相关的疾病、消费、健康等公众信息，从而预防和控制相关疾病，提高公众健康水平的科学。当前正在全球范围内流行的新冠疫情，更是将污水流行病学的应用扩展到对疫情的定性早期预警、对疾病流行率的定量估计以及疾病突发的定量警报，进一步拓展了污水流行病学的内涵。该方法有如下几个优点：1、监测的范围大、覆盖面广，可以评估大规模的社区总体的感染情况。市政污水厂通过污水管网承接了城市千家万户排放的污水，污水集水区域的人口数量少则千人，多则上百万人，覆盖的人口非常广泛，包括不能及时或者未发现症状而不进行核酸检测的感染者，因此能够更好的对疫情进行评估和预测。2、可预知病毒社区感染的重新爆发。由于污水新冠病毒的检测结果比临床患者出现早，因此会有预警作用。3、可作为疾病传播动态监测的辅助手段。对卫生监督结果进行有效的补充，这一点在中低收入的国家尤为重要。
  第一阶段问题：
  1. 请根据附注网站上的数据，研究美国污水监测采样点的分布是否合理？如果可以增加十个采样点，请建立数学模型，选择最合理的位置设置采样点。
  2. 请对数据进行分析，对于可能出现的大规模疫情进行预警，并给当地的政府写一封信（一或二页），说明对疫情的预判，对情况严重性的估计，并给出一定的防控建议。
  附注：数据下载网址:
  https://covid.cdc.gov/covid-data-tracker/#wastewater-surveillance

整体求解过程概述(摘要)

  本文针对污水监测采样点分布合理性问题，基于主成分分析分析法对 701 个污水监测采样点进行综合评价；随后，针对新增 10 个污水监测采样点最优选址问题，基于非线性离散动态规划对此构建决策模型，并且以启发式算法代替非线性规划模型进行求解，基于“逐步最优，得到整体最优解”的思想。最后，针对疫情爆发预警问题，基于典型相关性分析法和灰色关联法求解典型相关系数和灰色关联度系数分析疫情爆发与否。
  针对问题一：首先，我们对数据集进行特征提取与标注解析，增加经纬度坐标标注，扩建特征指标；随后，我们通过无监督 DBSCAN 聚类迭代搜寻出 701 个污水监测采样点的中心点，其经纬度（118.679、34.894），并引入欧式距离进行结果检验；其次，构建污水监测采样点分布特征指标体系，进行数据标准化处理及正负相关性处理；紧接着，为了探究七个特征指标是否适用于主成分分析，进行数据先验：KMO 检验和 Bartlett’s检验，其中 KMO 检验系数为 0.883 和 Bartlett’s 检验的 P 值小于 0.01，证明了七个特征指标适用于主成分分析；最后我们构建基于主成分分析法的污水监测采样点分布合理性综合评价模型，计算出每个污水监测采样点分布合理性综合评分，并列出 60 个分布合理性最高的采样点，统计可得，有 666 个采样点（占比为 95%）所得的分布合理性综合评分均高于 0.5，仅有 35 个采样点（占比为 5%）所得的分布合理性综合评分低于 0.5；得出结论：美国分布绝大部分污水监测采样点分布合理性极高。为了确定新增 10 个采样点的坐标，我们构建基于非线性离散动态规划的最优污水监测采用点选址决策模型，将 7 类特征指标均作为决策变量加入目标函数中，确定约束条件，将特征指标水平限制在对于区间范围内，最后我们基于粒子群算法求解迭代结果，得出 10 个采样点经纬度为：（116.839、45.143）（109.737、42.288）（117.832、38.202）（108.376、36.646）（94.026、42.233）（81.589、35.089）（86.078、34.482）（73.347、43.156）（81.921、39.496）（84.827、34.847），并利用皮尔逊相关系数热力图进行结果检验。
  针对问题二：首先，我们以会爆发大规模新冠肺炎疫情与不会爆发大规模新冠肺炎疫情作为两组典型变量，计算典型相关系数，并且进行显著性检验：𝑷 值检验与统计量检验；其次，得出结论：7 类特征指标的典型性相关系数均通过了显著性检验，其中，污水中当前病毒水平𝜂𝑡特征指标的典型相关系数最大，对大规模的新冠肺炎疫情的爆发起到影响作用也最大；医疗水平𝜇𝑡特征指标的典型相关系数较小；最后，我们利用灰色关联分析法求解灰色关联度系数，求和探究疫情的爆发与否。给出一封关于疫情预警、严重性估计、防控的建议信。
  我们对 DBSCAN 聚类进行𝑴𝒊𝒏𝑷𝒕𝒔和𝒆𝒑𝒔𝒊𝒍𝒐𝒏调参，分析模型的灵敏度；并且分析了本文模型的优缺点，提出了模型的推广和改善方向。

问题分析：

  本文主要从 701 个污水监测采样点的 7 个维度特征指标来分析美国污水监测采样点的分布合理性问题、新增污水监测采样点的选址问题以及地区中大规模的新冠肺炎疫情爆发预警问题。

  针对问题一：
  为了探究美国污水监测采样点的分布合理性以及如何新增 10 个污水监测采样点的选址问题。我们首先下载得到 wastewater_surveillance_data.csv 数据集，并且对数据集进行解析，并且初步统计分析，将 wastewater_surveillance_data.csv 数据集进行翻译解析，所得 15-Day Percent Change（15 天内变化百分比）、15-Day Detection Proportion（15 天内监测比例）的统计分布图以及数据表；紧接着对数据集经纬度坐标进行标注，并利用Geopandas 库进行绘制数据集中已知污水监测采样点经纬度统计表以及分布图；随后，我们对数据集进行了指标扩建，以人口数量、15 天内变化百分比、15 天内监测比例、区域流通水量、污水中当前病毒水平、与聚类采样点中心的距离、医疗水平 7 类特征指标为污水监测采样点分布特征指标体系的核心评价指标；利用无监督 DBSCAN 聚类实现采样点中心的经纬度空间定位，并且引入欧氏距离作为结果检验。通过构建污水监测采样点分布特征指标体系，并且将相关数据带入基于主成分分析法的污水监测采样点分布合理性评价模型中，求解采样点分布合理性综合评分，分析美国污水监测采样点的分布合理性；最后，构建基于非线性离散动态规划的最优污水监测采样点选址决策模型，并且利用粒子群算法迭代求解 10 个最优污水监测采样点经纬度坐标，并利用皮尔逊相关系数热力图进行结果检验。
  针对问题二：
  为了探究地区是否会爆发大规模新冠肺炎疫情，其影响因素有很多，若是想要对其进行及时预警，我们首先利用典型相关性法对污水监测采样点分布特征指标体系的核心评价指标进行因素解析，将会爆发大规模新冠肺炎疫情与不会爆发大规模新冠肺炎疫情作为两组典型变量，利用污水监测采样点分布特征指标体系中的 7 类特征指标数据得出典型相关系数，建立典型相关分析模型；随后，我们利用灰色关联分析法，以污水中当前病毒水平𝜂𝑡为参考数列，15 天内变化百分比水平𝛿𝑡、15 天内监测比例水平𝜀𝑡、人口数量𝜁𝑡、区域流通水量𝑄𝑡、与聚类采样点中心的距离𝜌𝑡共 6 类特征指标为比较数列，依次计算出每个污水监测采样点相对污水中当前病毒水平𝜂𝑡的灰色关联度系数，并且将计算所得 6 个灰色关联度系数相加求和，并且绘制灰色关联系数热力图进行结果检验。

模型假设：

  （1）假设人口不大规模流动，并且存在一定数量的现有感染者。
  （2）假设病毒对水的影响仅由监测收集的数据决定，不考虑其他人为干涉因素。
  （3）假设污水监测采样点的分布合理性仅由所搜集数据所反映的特征指标所决定，不考虑采样点自身其他主观因素。
  （4）假设没有新型类似的关联病毒出现，只有目标样本病毒。

模型的建立与求解

Data.Cdc.Gov 网站数据特征提取与标注解析

  为了探究污水流行病学原理在新冠疫情防控方面的作用，我们首先对题目所提供的Data.Cdc.Gov 网站中的相关数据进行特征提取与标注解析，做出初步的分析，为后续构建污水监测采样点分布特征指标体系增加合理性与可行性。
  wastewater_surveillance_data.csv 数据集解析：
  于 Data.Cdc.Gov 网站中，我们下载可得wastewater_surveillance_data.csv 数据集，其中包含：Jurisdiction（管辖区域）、Sewershed ID（排水管编号）、Reporting Jurisdiction（报告管辖区域）、County（所在区县）、Population Served（人口数量）、15-Day Percent Change（15 天内变化百分比）、15-Day Detection Proportion（15 天内监测比例），共 7 列元素、701 个污水监测采样点。
  经过初步统计分析，将 wastewater_surveillance_data.csv 数据集进行翻译解析，所得15-Day Percent Change（15 天内变化百分比）、15-Day Detection Proportion（15 天内监测比例）统计分布图以及数据表，如下所示：

  其中，总的污水监测采样点总数为 747 个；当前有数据变化的污水监测采样点总数为 458 个。

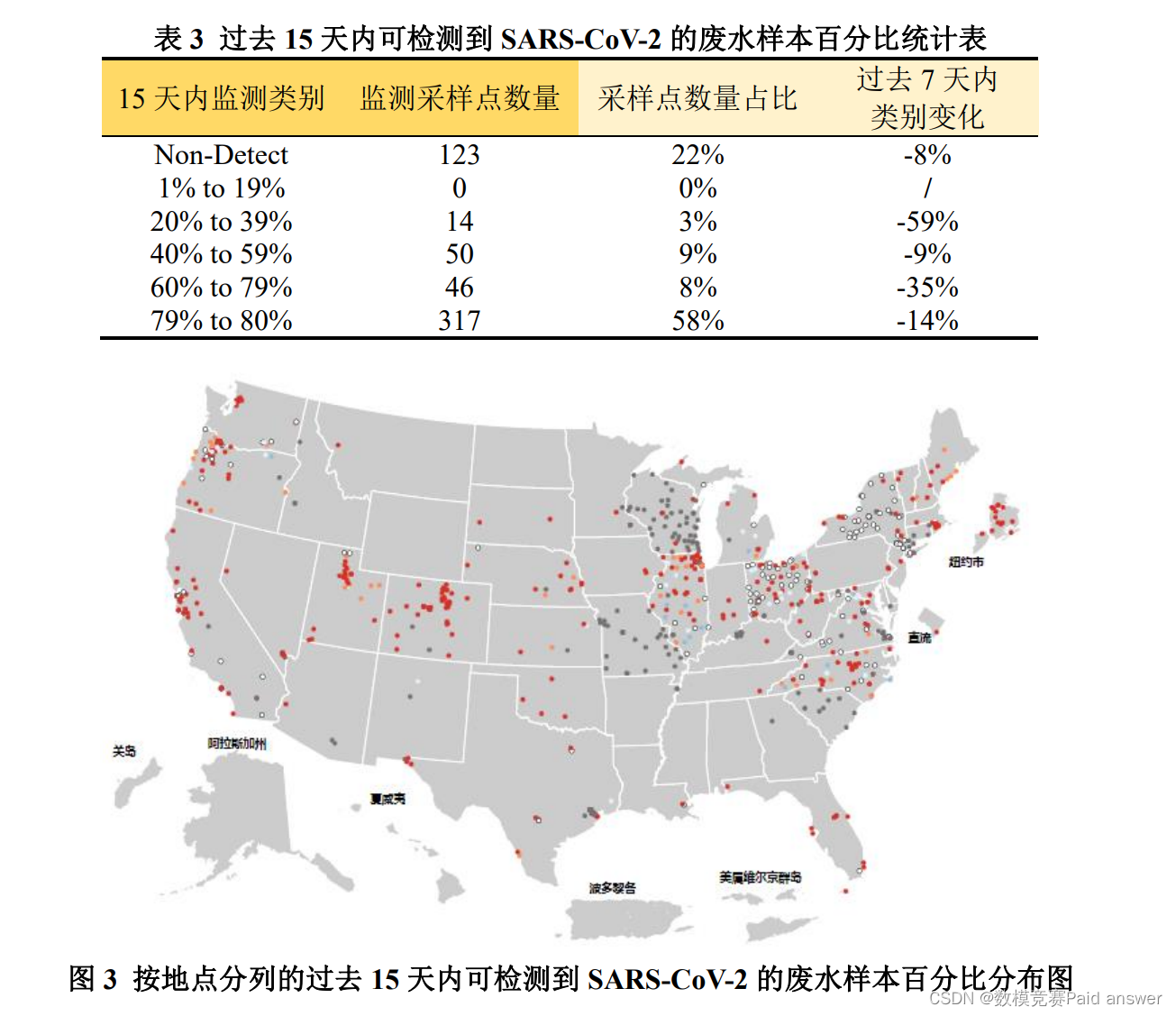
  其中，总的污水监测采样点总数为 747 个；当前有数据变化的污水监测采样点总数为 550 个。
  wastewater_surveillance_data.csv 数据集经纬度坐标标注：
  为了后续的污水监测采样点的地理位置分析，我们利用 Map Location 在线网站为wastewater_surveillance_data.csv 数据集中的 701 个污水监测采样点标注经纬度坐标。部分经纬度标注数据统计表（由于篇幅问题，正文仅展示部分），如下所示：

  同时为了验证根据经纬度坐标在地图上精准定位的可行性，以便后续根据动态优化求得新增 10 个污水监测采样点的经纬度坐标来反推采样点在美国地图的具体位置。为此，我们利用 Python 的内置库 Geopandas 进行绘制数据集中的 8 个已知污水监测采样点经纬度统计表以及分布图，如下所示：

  wastewater_surveillance_data.csv 数据集指标扩建：
  由于污水监测是以污水流行病学（Wastewater-Based Epidemiology，WBE）的原理为手段，并且通过分析市政污水处理厂进水中的污染物或者生物标记物浓度，结合人体代谢机理、进水流量和服务人群数量等信息，反推该物质在污水集水区内的状况。
  因此为了确定美国污水监测采样点的分布是否合理，仅靠已有数据集中的特征指标无法科学地分析美国污水监测采样点分布的合理性。
  对此，我们将为 wastewater_surveillance_data.csv 数据集进行特征指标扩建，添加相关特征指标，重构污水监测采样点分布特征指标体系。
  除开数据集中已有的 Jurisdiction（管辖区域）、Sewershed ID（排水管编号）、Reporting Jurisdiction（报告管辖区域）、County（所在区县）、Population Served（人口数量）、15-Day Percent Change（15 天内变化百分比）、15-Day Detection Proportion（15 天内监测比例），我们增加经度坐标、纬度坐标、区域流通水量、污水中当前病毒水平、与聚类采样点中心的距离、医疗水平（以美国北卡罗莱纳沃塔的医疗水平为基准线，超过即为正；反之，则为负）6 类特征指标；
  同时，以人口数量、15 天内变化百分比、15 天内监测比例、区域流通水量、污水中当前病毒水平、与聚类采样点中心的距离、医疗水平 7 类特征指标为污水监测采样点分布特征指标体系的核心评价指标。

无监督 DBSCAN 聚类实现采样点中心经纬度空间定位

  为了计算污水监测采样点分布特征指标体系中每个坐标点与聚类采样点中心的距离以及后续新增 10 个污水监测采样点的地址分布，我们首先利用无监督机器学习算法中的 DBSCAN 聚类算法，经过 701 次迭代，实现精准定位污水监测采样点中心的经纬度。
  DBSCAN 聚类算法概述：
  DBSCAN 是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，DBSCAN 算法将“簇”定义为密度相连的点的最大集合。
  DBSCAN 聚类算法的核心概念：


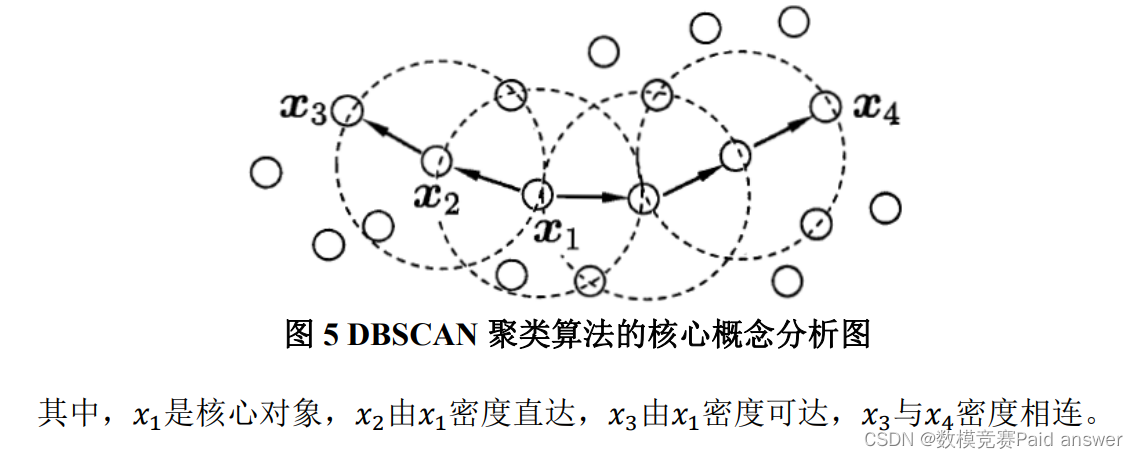
  求解过程：
  设置参数𝑀𝑖𝑛𝑃𝑡𝑠 = 4和𝑒𝑝𝑠𝑖𝑙𝑜𝑛 = 1.00。以 wastewater_surveillance_data.csv 数据集中的每个污水监测采样点为样本点，并且以每个污水监测采样点为中心，探寻其𝑟邻域来搜索簇。

  当某个样本点的𝑟邻域包含多于𝑀𝑖𝑛𝑃𝑡𝑠个样本点时，则创建一个以该样本点为核心对象的簇；进行不断迭代，聚集从这些核心对象直接密度可达的对象，包括一些密度可达簇的合并过程。当没有新的簇产生时，迭代过程结束。
  以𝑀𝑖𝑛𝑃𝑡𝑠 = 4和𝑒𝑝𝑠𝑖𝑙𝑜𝑛 = 1.00为参数设定，我们对所实例化构建的 DBSCAN 聚类模型进行迭代；当迭代次数达到 701 次时，污水监测采样点样本集中没有新的簇产生，于是迭代过程结束，并且实现精准定位污水监测采样点中心的经纬度为：经度（118.679）、纬度（34.894）。
  以纽约市的 45 个污水监测采样点的聚类过程为例，具体过程如下所示：
  以下是纽约市原始过去 15 天内 SARS-CoV-2 按采样点变化百分比分布图和按地点分列的过去 15 天内可检测到 SARS-CoV-2 的废水样本百分比分布图，如下所示：


  图解：
  其中，红色圆圈代表该污水监测采样点𝑟邻域所生成的簇；蓝色圆圈代表污水监测采样点为离群点；绿色圆圈代表该污水监测采样点𝑟邻域为密度可达或密度直达。
  结果分析：
  对纽约市的45个污水监测采样点进行多次迭代，模型从样本集的左下角开始搜寻，起初几次迭代只能搜寻少许生成簇和离群点；随着迭代次数的增加，搜寻所得的生成簇的个数不断增加，逐渐可以搜寻到密度可达或密度直达的存在；直到最终将所有离群点、生成簇、密度可达、密度直达搜寻完毕，迭代结束。
  搜寻所得纽约市的 45 个污水监测采样点的中心采样点的经纬度坐标分别如下：经度（118.679）、纬度（34.894）。具体分布图，如下所示：

污水监测采样点分布特征指标体系的构建

  为了分析美国污水监测采样点的分布合理性，我们需要对此进行综合评价分析。在此之前，我们需要构建污水监测采样点分布特征指标体系。
  我们以人口数量、15 天内变化百分比、15 天内监测比例、区域流通水量、污水中当前病毒水平、与聚类采样点中心的距离、医疗水平 7 类特征指标为污水监测采样点分布特征指标体系的核心评价指标。
  污水监测采样点分布特征指标体系构建图，如下所示：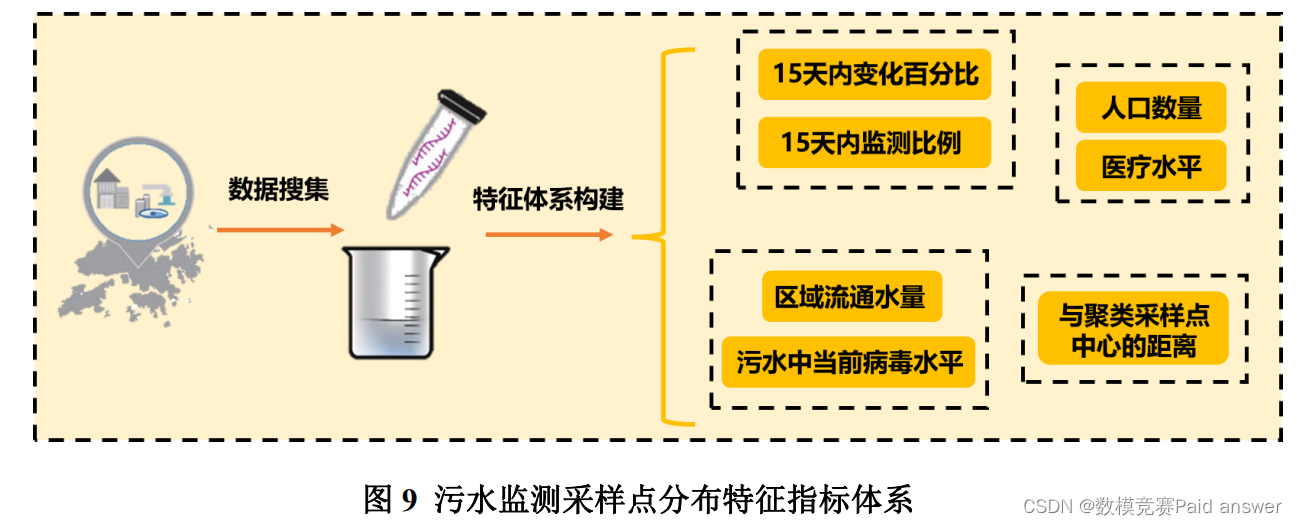

  由图分析可知，当某个污水监测采样点的 15 天内变化百分比水平越高、15 天内监测比例水平越高、人口数量越多、区域流通水量越大、污水中当前病毒水平越高、与聚类采样点中心的距离越近、医疗水平越低时，越容易发生大规模疫情，造成大规模人口
感染，值得预警。
  当某个污水监测采样点越符合上述 7 种情况，则该污水监测采样点的分布合理性越高。

  数据正负相关性处理：
  由于我们利用主成分分析综合评价模型对美国污水监测采样点的分布合理性进行分析，因此在综合评价的应用之前，我们需要明确各个传入参数指标的正负相关性，并且做好相关处理。

基于主成分分析法的污水监测采样点分布合理性评价模型

  通过搜集所得相关数据和已经建立的污水监测采样点分布特征指标体系，可以发现污水监测采样点分布的合理性评价与七个特征指标有着必然联系；并且众多指标之间存在复杂的相关性，增加了量化分析的复杂度。
  单独对每个指标进行分析，往往会将指标孤立化，不能够完全利用数据中的信息，盲目导致指标损失许多有用的信息，从而产生错误的结论。
  因此我们采用主成分分析法来建立污水监测采样点分布合理性评价模型。
  数据先验：
  为了更好地应用主成分分析, 我们需要对主成分分析结果进行统计检验并建立统计检验体系。其中不可或缺的一步便是主成分适用性检验，即该七个特征指标数据是否适合使用主成分方法进行分析[2]。
  KMO 检验是从比较原始变量之间的简单相关系数和偏相关系数的相对大小出发来进行的检验。当所有变量之间的偏相关系数的平方和, 远远小于所有变量之间的简单相关系数的平方和时, 变量之间的偏相关系数很小, KMO 值接近 1, 变量适合进行主成分分析。
  Bartlett’s 检验的原假设是研究数据之间的相关矩阵是一个完美矩阵，即所有对角线上的系数为 1，非对角线上的系数均为 0。在这种完美矩阵的情况下，各变量之间没有相关关系，即不能将多个变量简化为少数的成分，没有进行主成分提取的必要。因此，我们希望拒绝 Bartlett’s 检验的零假设，即 Bartlett’s 检验的 P 值小于 0.01。
  我们利用 SPSS 软件，对七个特征指标进行 KMO 检验和 Bartlett’s 检验，结果表如下：

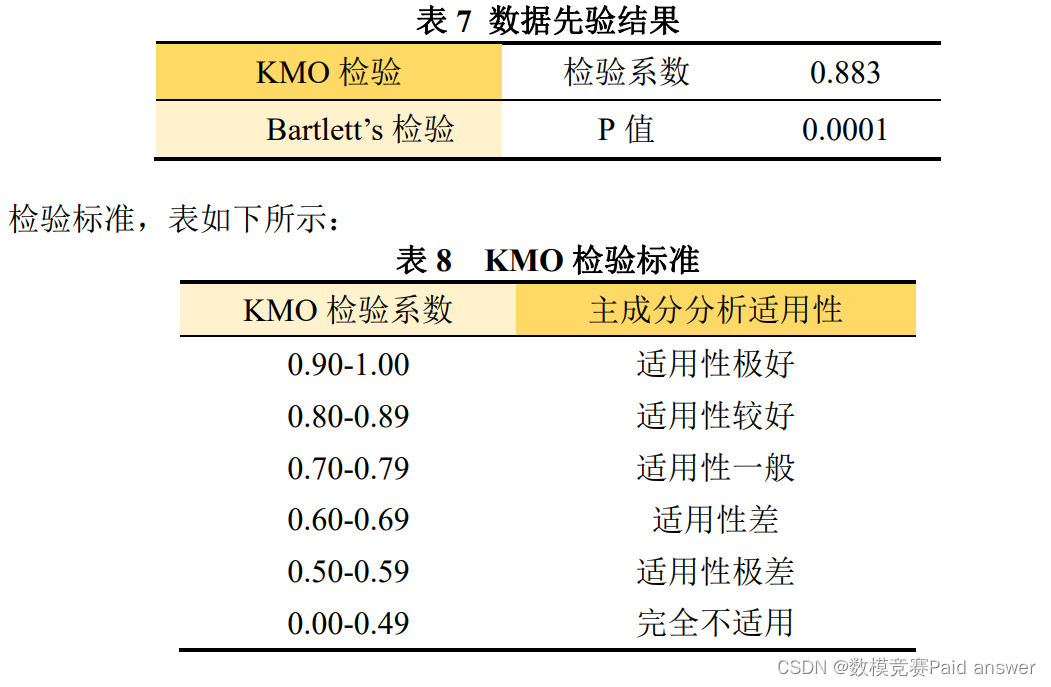
  根据检验结果表和检验标准表可知，KMO 检验系数为 0.883，代表将七个特征指标应用于主成分分析的适用性较好；并且 Bartlett’s 检验的 P 值小于 0.01，拒绝了零假设；因此，七个特征指标之间具有相关关系，能够进行主成分分析。

求解：

  我们首先运用 Python 软件对搜集所得数据进行指标构建，得到 7 个特征指标；随后我们依据主成分分析法的算法流程，运用 Matlab 软件进行编程，对 7 个特征指标进行主成分分析；求得相关系数矩阵的 7 个特征根、贡献率、累计贡献率，如下表所示：

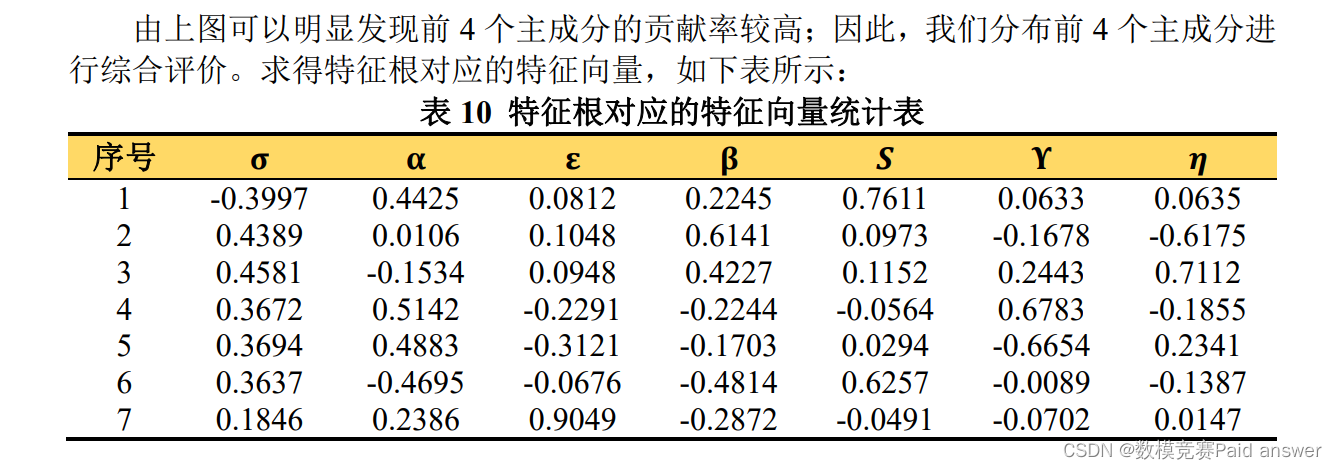
基于非线性离散动态规划的最优污水监测采样点选址决策模型

  分析完美国污水监测采样点的分布合理性问题，我们需要根据已有的 701 个污水监测采样点分布特征，确定并且新增 10 个污水监测采样点。
  由于每个污水监测采样点管辖范围内的服务人口数量、医疗水平差异较大，以及污水中当前病毒水平、区域流通水量各不相同，造成现有污水监测采样网络系统的预警工作不够完善，导致部分地区无法精准预警疫情的发生。
  因此，我们需要确定并且新增 10 个污水监测采样点来链接原有的污水监测采样网络系统，来解决这一问题。

构建非线性离散动态规划模型：

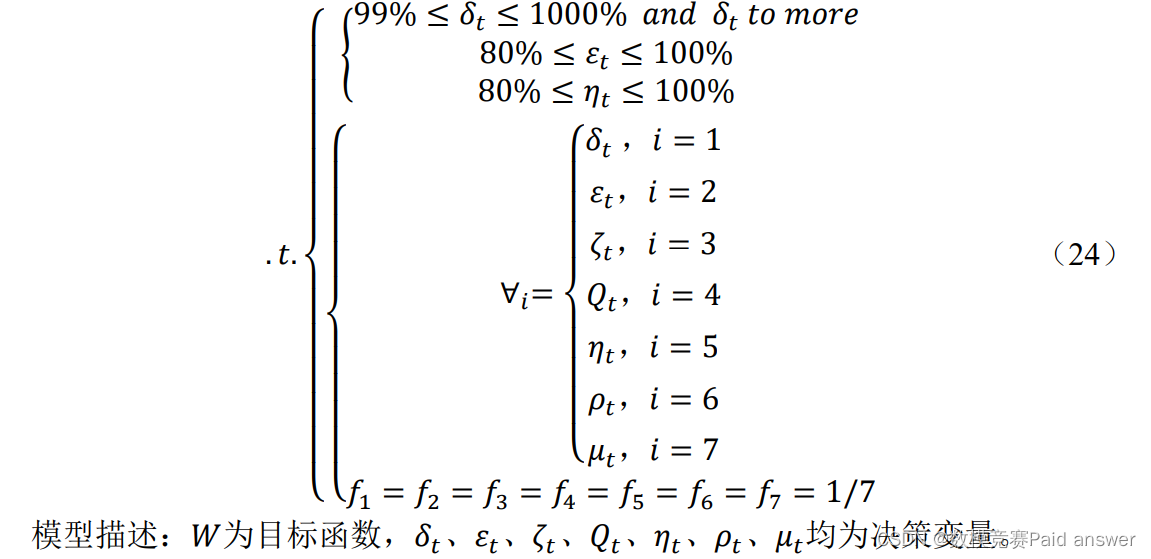
  求解结果展示：
  我们利用 Python 软件编程，按照上述求解流程进行求解，通过 1000 次的迭代，计算得出新增 10 个污水监测采样点的具体经纬度坐标。其中，粒子群算法的迭代过程（迭代概念图+迭代实际效果图），如下所示：


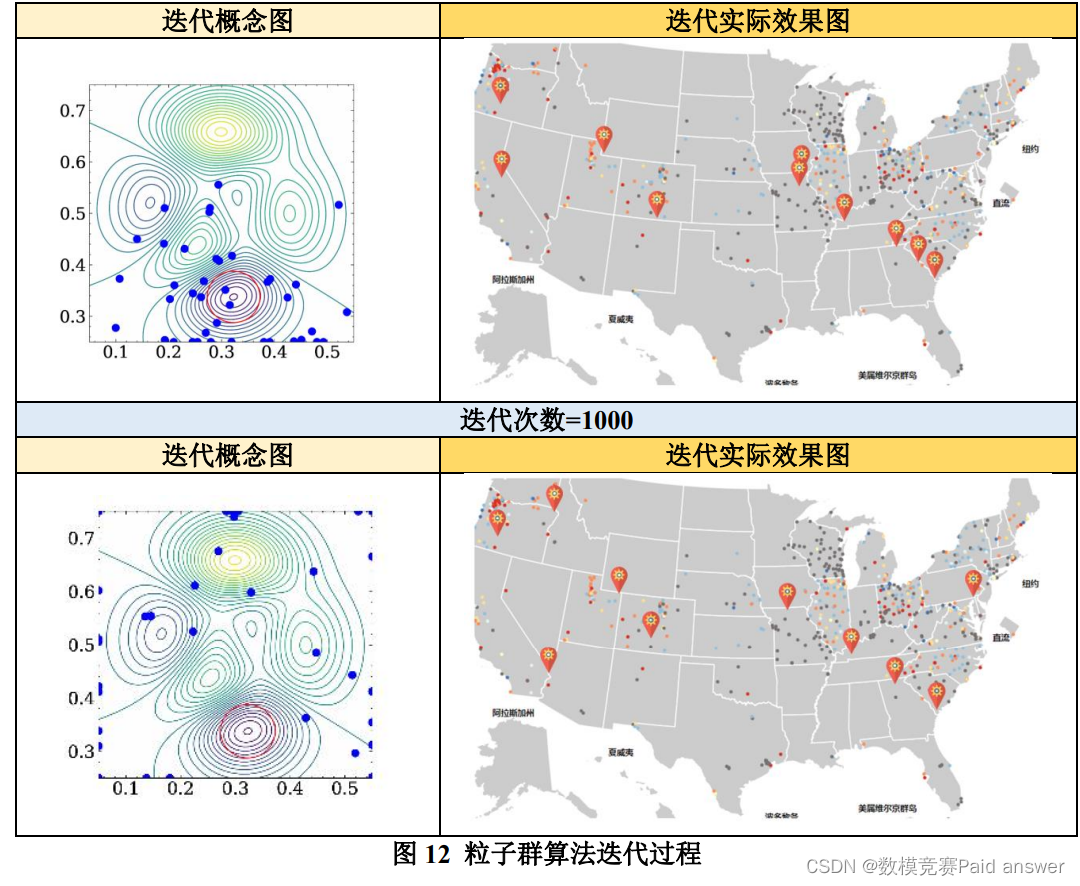
  通过观察上图，我们可以发现经过 1000 次迭代之后，所有粒子均已收敛，说明通过粒子群算法的求解，已经得到 10 个污水监测采样点的最优选址方案。最优选址方案，如下所示：

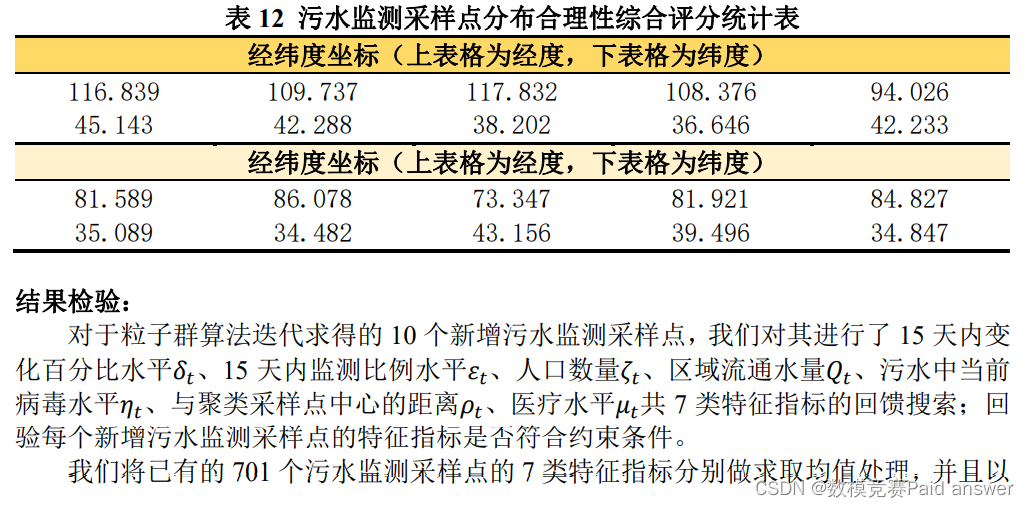
基于典型相关性分析法的因素解析

  决定地区是否会爆发大规模新冠肺炎疫情的影响因素有很多，若是想要对可能出现的大规模疫情进行及时预警，我们首先需要在具有代表性的 7 类特征指标：15 天内变化百分比水平、15 天内监测比例水平、人口数量、区域流通水量、污水中当前病毒水平、与聚类采样点中心的距离、医疗水平中做典型相关性分析，判断每类特征指标对大规模新冠肺炎疫情的爆发是否具有极高的影响力。
  我们将会爆发大规模新冠肺炎疫情与不会爆发大规模新冠肺炎疫情作为两组典型变量，利用污水监测采样点分布特征指标体系中的7类特征指标数据得出典型相关系数，建立典型相关分析模型，取临界值𝜏 = 0.5。

  求解过程：
  首先我们计算出各个指标的典型相关系数，再对结果进行显著性检验，检验典型相关分析法的适用性是否良好。求解过程如下所示：
𝑆𝑡𝑒𝑝1：求解典型相关系数
  我们根据污水监测采样点分布特征指标体系中的 7 类特征指标的相关数据，利用协方差矩阵和相关系数矩阵，解出各个指标的典型相关系数，结果，如下所示：

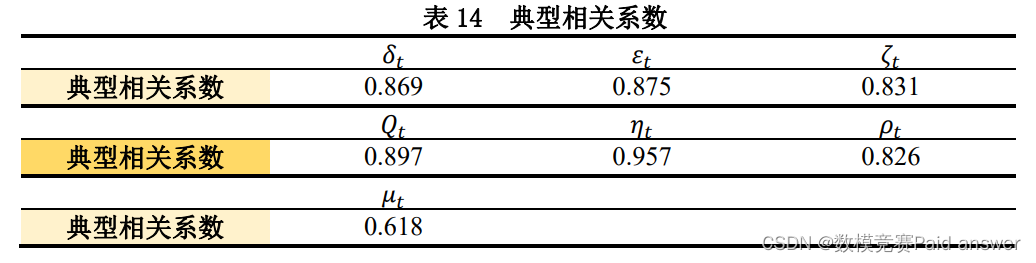
𝑆𝑡𝑒𝑝2：显著性检验
  在典型相关系分析模型中我们使用的检验方法是 𝑷 值检验与统计量检验。
  𝑃值即为(零假设的)拒绝域的面积或概率。用𝑃值做判断与检验统计量做判断得出的结论是完全一样的。
  在检验中有两种方法：第一种，检验统计量是否落在拒绝域中；第二种，𝑃值是否小于显著性水平。
  其实两种判断是等价的，拒绝域是根据显著性水平计算出来的，然后看检验统计量与拒绝域比较；而𝑃值是根据检验统计量算出来的，然后看𝑃值与显著性水平比较。在分布图上，𝑃值所在位置就是检验统计量所在位置。

  因此，得出结论：7 类特征指标的典型性相关系数均通过了显著性检验，都对大规模的新冠肺炎疫情的爆发起到影响作用；其中，污水中当前病毒水平𝜂𝑡特征指标的典型相关系数最大，对大规模的新冠肺炎疫情的爆发起到影响作用也最大；医疗水平𝜇𝑡特征指标的典型相关系数较小，在后续的处理中，不再采用该特征指标。

基于灰色关联分析的新冠肺炎疫情爆发分析模型

  为了对大规模新冠肺炎疫情爆发的预警，我们利用灰色关联分析法，以污水中当前病毒水平𝜂𝑡为参考数列，15 天内变化百分比水平𝛿𝑡、15 天内监测比例水平𝜀𝑡、人口数量𝜁𝑡、区域流通水量𝑄𝑡、与聚类采样点中心的距离𝜌𝑡共 6 类特征指标为比较数列。
  依次计算出每个污水监测采样点相对污水中当前病毒水平𝜂𝑡的灰色关联度系数，并且将计算所得 6 个灰色关联度系数相加求和。若是灰色关联度系数的求和值越小，说明新冠肺炎疫情爆发于其之间的相关性较弱，爆发疫情的可能性越小；反之，说明新冠肺炎疫情爆发于其之间的相关性较强，爆发疫情的可能性越大。通过灰色关联分析法，实现对大规模的新冠肺炎疫情的及时预警。
  求解：
  计算灰色关联系数（由于篇幅问题，正文中仅展示部分），并且绘制灰色关联系数热力图，如下所示：

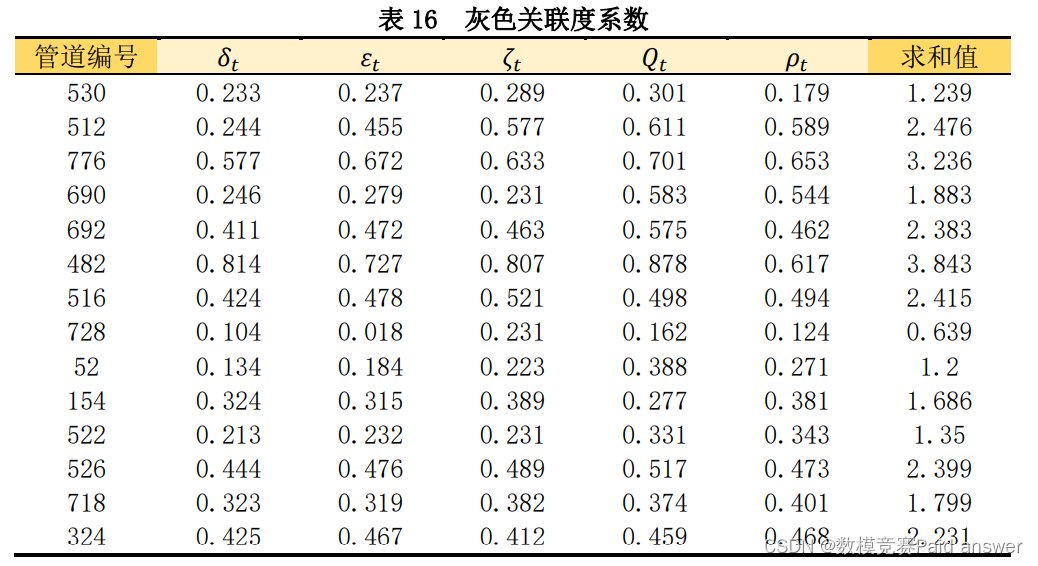
  由表 16 可以得出 482 号管道 6 个灰色关联度系数的求和值达到 3.843，说明新冠肺炎疫情爆发于其之间的相关性较强，爆发疫情的可能性较大；728 号管道的 6 个灰色关联度系数的求和值仅为 0.639，说明新冠肺炎疫情爆发于其之间的相关性较弱，爆发疫情的可能性较小。

论文缩略图：

程序代码：

import pandas as pd
import numpy as np
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
import seaborn as sns
import folium
from sklearn import metrics
from math import radians
from math import tan,atan,acos,sin,cos,asin,sqrt
from scipy.spatial.distance import pdist, squareform
sns.set()
def haversine(lonlat1, lonlat2):
 lat1, lon1 = lonlat1
 lat2, lon2 = lonlat2
 lon1, lat1, lon2, lat2 = map(radians, [lon1, lat1, lon2, lat2])
 dlon = lon2 - lon1
 dlat = lat2 - lat1
 a = sin(dlat / 2) ** 2 + cos(lat1) * cos(lat2) * sin(dlon / 2) ** 2
 c = 2 * asin(sqrt(a))
 r = 6371 # Radius of earth in kilometers. Use 3956 for miles
 return c * r * 1000
df = pd.read_csv('00-污水监测数据.csv')
df = df[['lat_Amap', 'lng_Amap']].dropna(axis=0,how='all')
# df['lon_lat'] = df.apply(lambda x: [x['lng_Amap'], x['lat_Amap']], axis=1)

# df = df['lon_lat'].to_frame()
# data = np.array(data)
# plt.figure(figsize=(10, 10))
# plt.scatter(df['lat_Amap'], df['lng_Amap'])
distance_matrix = squareform(pdist(df, (lambda u, v: haversine(u, v))))
db = DBSCAN(eps=500, min_samples=10, 
metric='precomputed').fit_predict(distance_matrix)
'''
db = DBSCAN(eps=0.038, min_samples=3).fit(data)
'''
labels = db
raito = len(labels[labels[:] == -1]) / len(labels) # 计算噪声点个数占总数的比例
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) # 获取分簇的数目
# score = metrics.silhouette_score(distance_matrix, labels)
df['label'] = labels
sns.lmplot('lat_Amap', 'lng_Amap', df, hue='label', fit_reg=False)
''' 
df['label'] = labels
sns.lmplot('lat_Amap', 'lng_Amap', df, hue='label', fit_reg=False)
'''
map_all = folium.Map(location=[31.574729, 120.301663], zoom_start=12,
 
tiles='http://webrd02.is.autonavi.com/appmaptile?lang=zh_cn&size=1&scale=1&style=7&
x={x}&y={y}&z={z}',
 attr='default')
# colors = ['#DC143C', '#FFB6C1', '#DB7093', '#C71585', '#8B008B', '#4B0082', 
'#7B68EE',
# '#0000FF', '#B0C4DE', '#708090', '#00BFFF', '#5F9EA0', '#00FFFF', 
'#7FFFAA',
# '#008000', '#FFFF00', '#808000', '#FFD700', '#FFA500', '#FF6347', 
'#000000']
colors = ['#DC143C', '#FFB6C1', '#DB7093', '#C71585', '#8B008B', '#4B0082', 
'#7B68EE',
 '#0000FF', '#B0C4DE', '#708090', '#00BFFF', '#5F9EA0', '#00FFFF', 
'#7FFFAA',
 '#008000', '#FFFF00', '#808000', '#FFD700', '#FFA500', 
'#FF6347','#DC143C', 
 '#FFB6C1', '#DB7093', '#C71585', '#8B008B', '#4B0082', '#7B68EE',
 '#0000FF', '#B0C4DE', '#708090', '#00BFFF', '#5F9EA0', '#00FFFF', 
'#7FFFAA',
 '#008000', '#FFFF00', '#808000', '#FFD700', '#FFA500', '#FF6347', 
 '#DC143C', '#FFB6C1', '#DB7093', '#C71585', '#8B008B', '#4B0082', 
'#7B68EE',
 '#0000FF', '#B0C4DE', '#708090', '#00BFFF', '#5F9EA0', '#00FFFF',
 '#7FFFAA',
 '#008000', '#FFFF00', '#808000', '#FFD700', '#FFA500', '#FF6347',
 '#DC143C', '#FFB6C1', '#DB7093', '#C71585', '#8B008B', '#4B0082', 
'#7B68EE',
 '#0000FF', '#B0C4DE', '#708090', '#00BFFF', '#5F9EA0', '#00FFFF', 
'#7FFFAA',
 '#008000', '#FFFF00', '#808000', '#FFD700', '#FFA500', 
'#FF6347','#DC143C', 
 '#FFB6C1', '#DB7093', '#C71585', '#8B008B', '#4B0082', '#7B68EE',
 '#0000FF', '#B0C4DE', '#708090', '#00BFFF', '#5F9EA0', '#00FFFF', 
'#7FFFAA',
 '#008000', '#FFFF00', '#808000', '#FFD700', '#FFA500', '#FF6347', 
 '#DC143C', '#FFB6C1', '#DB7093', '#C71585', '#8B008B', '#4B0082', 
'#7B68EE',
 '#0000FF', '#B0C4DE', '#708090', '#00BFFF', '#5F9EA0', '#00FFFF', 
'#7FFFAA',
 '#008000', '#FFFF00', '#808000', '#FFD700', '#FFA500', 
'#FF6347','#000000']
for i in range(len(df)):
 if labels[i] == -1:
 continue
 else :
 folium.CircleMarker(location=[df.iloc[i,0], df.iloc[i,1]],
 radius=4, popup='popup',
color=colors[labels[i]], fill=True,
fill_color=colors[labels[i]]).add_to(map_all)
 
map_all.save('all_cluster.html')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97