【学习笔记】《模式识别》3：线性分类器

线性分类器

一、判别函数

1. 定义

2. 与聚类准则函数的区别

• 聚类准则函数
  用于度量模式间的相似性；
  取极值，代表聚类达到最优解；
  自变量是样本集

• 判别函数
  取值直接决定样本的类别；
  自变量是单个样本

3. 关键问题

• 确定判别函数的形式，判别函数可以是线性或是非线性，取决于样本分布；
• 确定权重

二、线性判别函数

1. 一般形式

2.性质

3. 三种多类情况介绍

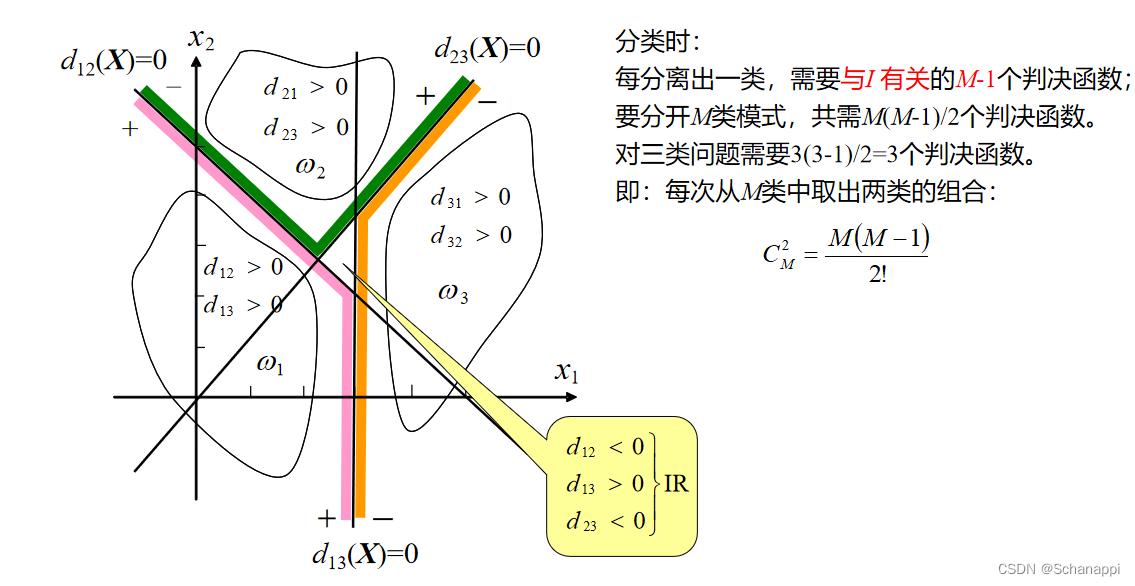
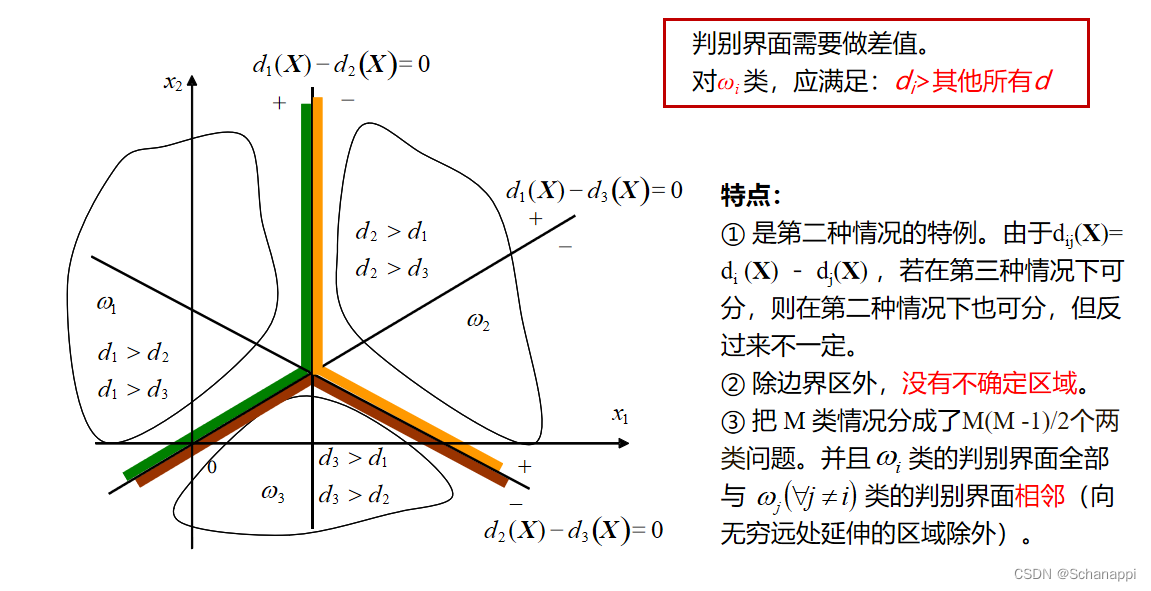
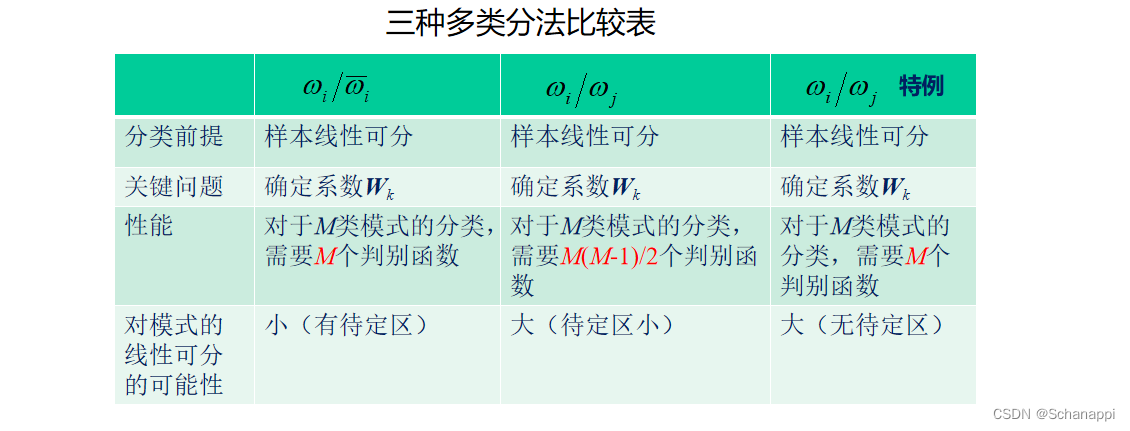
三、广义线性判别函数

1.目的

对非线性边界：通过某映射，把模式空间X变成X*，以便将X空间中非线性可分的模式集，变成在X*空间中线性可分的模式集。

2.非线性多项函数式

四、线性判别函数的几何性质

1.模式空间与超平面

（1）定义
模式空间以n维模式向量X的n个分量为坐标变量的欧式空间，用点、有向线段表示。
超平面，即判别函数d(X)=0。

（2）讨论

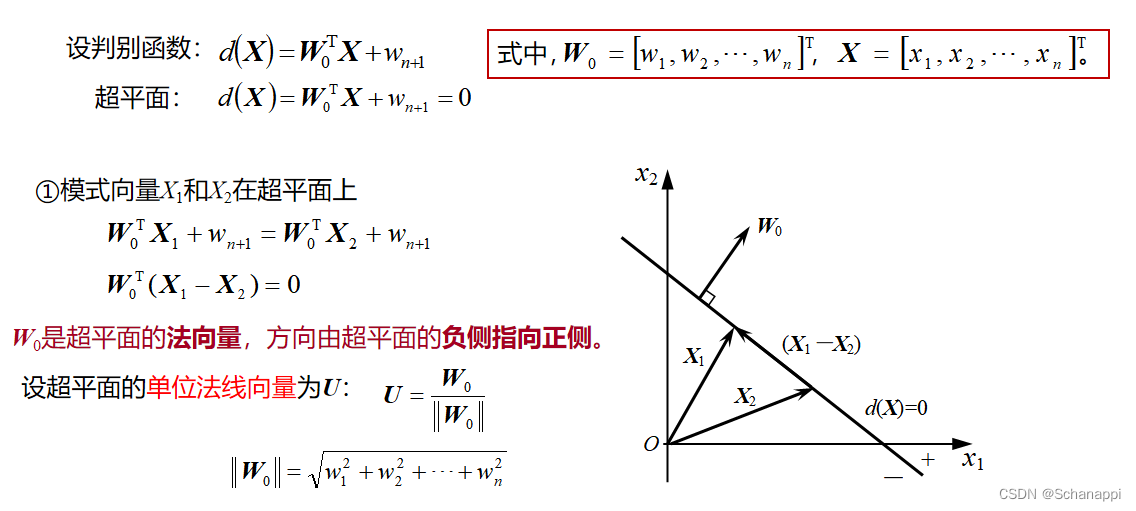
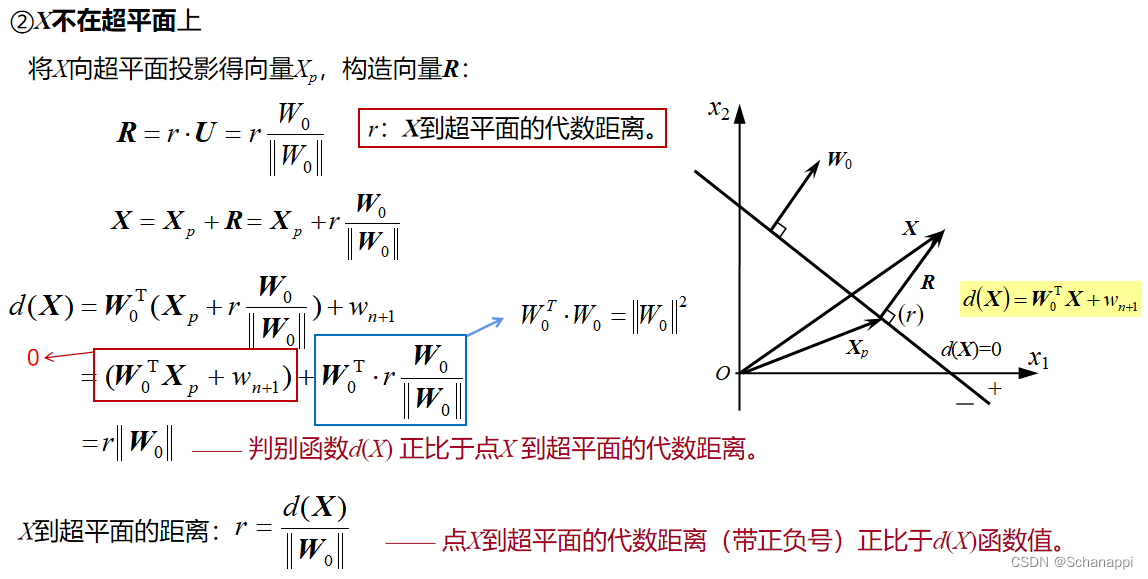
2.权空间与权向量解

（1）定义
权空间，以线性判别函数的权值为坐标变量的n+1维欧式空间；
増广权向量，w=(w₁,w₂,…w_n,w_n+1)^T，对应权空间的一个点，或者原点到该点的有向线段。

3.权重确定

感知器算法、梯度算法、最小平方误差算法

4.线性分类器的设计步骤

五、感知器算法

1.感知器

一种分类学习机模型，其“赏罚概念”得到广泛应用，但无法实现非线性分类。

2.感知器算法原理

3.算法步骤

4.收敛性

感知器算法是收敛的，经过有限次迭代运算后，能求出一个使所有样本都正确分类的W。

但是感知器算法的解不是单值的。

5.感知器算法应用于多类情况

计算题总结：

• 每一次迭代考虑一个w_i 类，使得d_i > 任意d_j均成立，此时才不需要更改权向量，否则就需要调整权向量；
• 每个类依次迭代，除非所有类都正确分类。
• 注意计算w_i类的时候，判别函数也都需要乘以该X，调整权向量的时候也都是用到该X。

六、梯度法

1.梯度概念

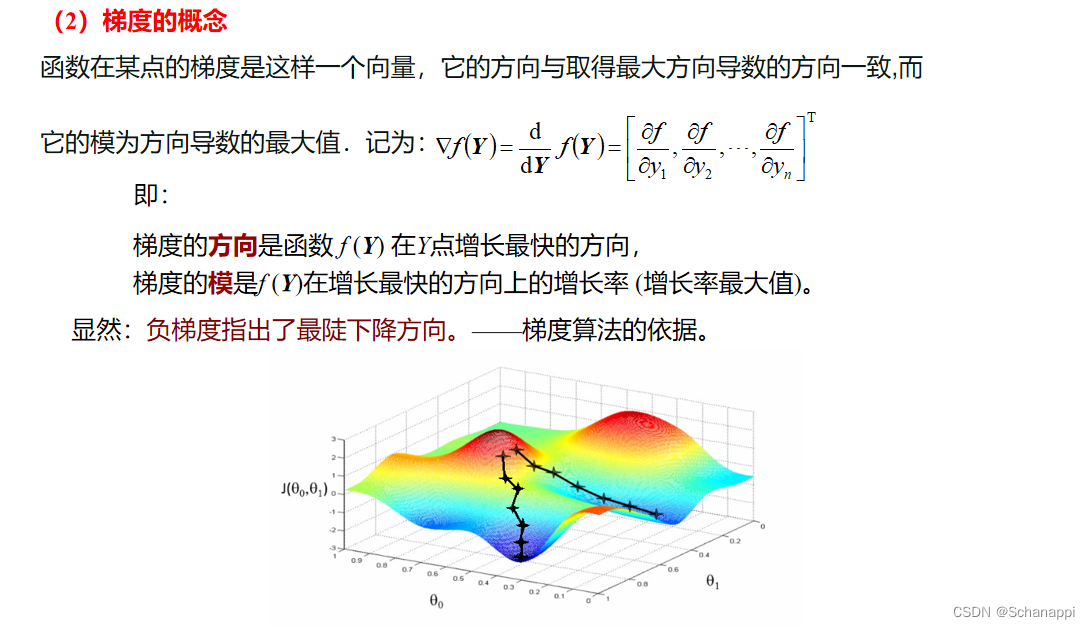
2. 梯度算法

3. 固定增量算法

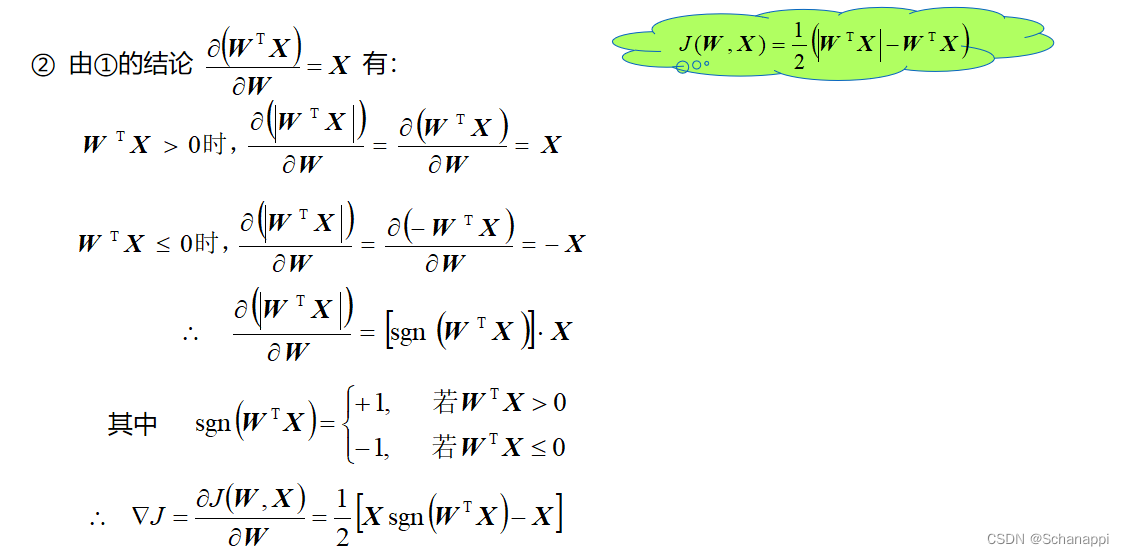
七、最小平方误差算法

最小平方误差算法（least mean square error, LMSE；亦称Ho-Kashyap算法）

感知器算法、梯度算法、固定增量算法或其他类似方法，只有当模式类可分离时才收敛，在不可分的情况下，算法会来回摆动，始终不收敛。
造成不收敛现象的原因有两种可能：

• 迭代过程本身收敛缓慢
• 模式不可分

1.LMSE算法特点

• 对可分模式收敛；
• 对于类别不可分的情况也能指出来。

2.原理

3.不等式方程XW>0的转换

4. 准则函数的计算

5.递推公式的推导

6. 模式类别可分性判别

7. 算法步骤

计算题总结：
难点在于X^# 的计算，需要求矩阵的行列式，求逆运算，可以通过两道例题进行复习。

8. 小结

要获得一个有较好判别性能的线性分类器，需要确定训练样本的数目。

用指标二分法能力N₀来确定训练样本的数目：N₀=2（n+1），其中n为模式维数。训练样本的数目不能低于N₀ ，通常为 N₀的5~10倍左右。

八、势函数法

1. 定义

划分属于ω1和ω2类模式样本：样本是模式空间中的点，将每个点比拟为点能源，在点上势能达到峰值，随着与该点距离的增大，势能分布迅速减小。

• ω1类样本势能为正——势能积累形成 “高地”
• ω2类样本势能×(-1)——势能积累形成 “凹地”

在两类电势分布之间，选择合适的等势面（如零等势面），就是判别界面。

2. 判别函数计算

3. 势函数

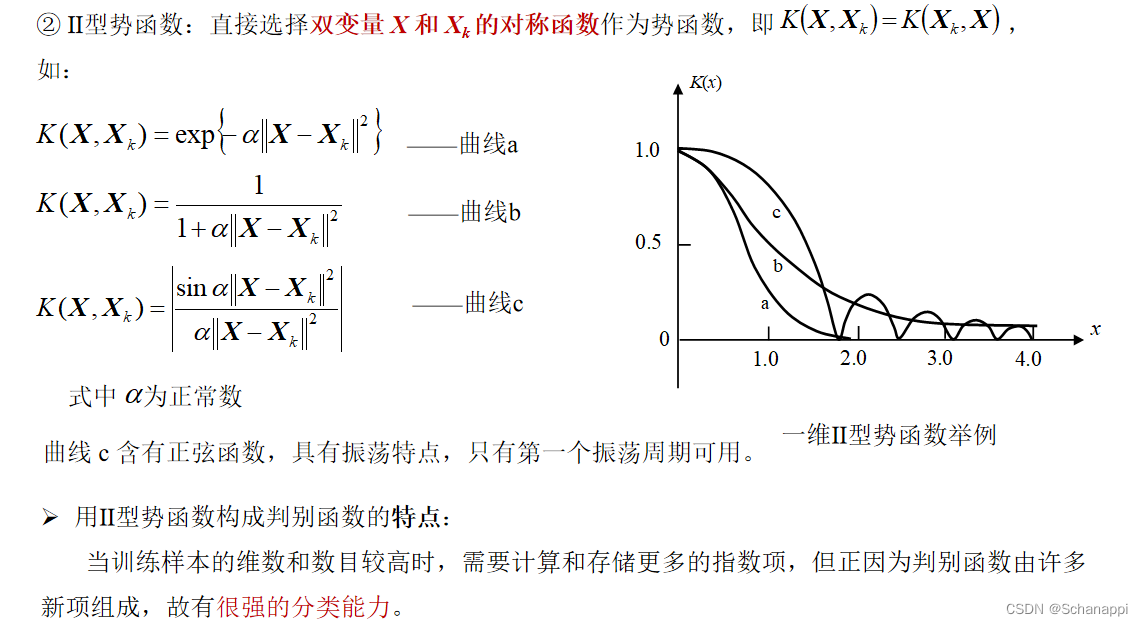
计算题总结
例题给出了II型势函数的示例，注意判断修正情况。