怪兽存活概率问题

怪兽存活概率问题

作者：Grey

原文地址：

博客园：怪兽存活概率问题

CSDN：怪兽存活概率问题

题目描述

给定3个参数，N，M，K 怪兽有 N 滴血，等着英雄来砍自己，英雄每一次打击，都会让怪兽流失，
怪兽每一次流失的血量在区间[0……M]上等概率的获得一个值，求 K 次打击之后，英雄把怪兽砍死的概率。

主要思路

由题目含义可知：怪兽在经历 K 次打击后所有可能的掉血情况有 (M+1) 的 K 次方种，，即：

long all = (long) Math.pow(M + 1, K)
1

如果怪兽在 K 次打击后，被砍死的情况有 kill 种，那么

(double) kill / (double) all;
1

即为怪兽被砍死的概率。

暴力解法

定义递归函数

long process(int times, int M, int hp)
1

递归含义是：怪兽还剩 hp 点血，每次的伤害在[0……M]范围上，还有 times 次可以砍，返回砍死的情况数。

那么 base case 有如下两种情况

// 情况一：已经没有被砍的次数了，这个时候，血量如果正好是小于等于0的值， 说明怪兽已经被砍死一次
// 否则怪兽不可被砍死
if (times == 0) {
    return hp <= 0 ? 1 : 0;
}
// 情况二：怪兽已经死了，但是还可以砍
// 此时，所有的砍法都满足条件，所以情况就是(long) Math.pow(M + 1, times)
if (hp <= 0) {
    return (long) Math.pow(M + 1, times);
}
1
2
3
4
5
6
7
8
9
10

接下来就是普遍情况，由于每次攻击是 [0……M] 中等概率的一个值，则枚举从 0 到 M 任意一个值跑递归函数即可。

long ways = 0;
for (int i = 0; i <= M; i++) {
    ways += process(times - 1, M, hp - i);
}
1
2
3
4

完整代码如下

public class Code_KillMonster {
    public static double right(int N, int M, int K) {
        if (N < 1 || M < 1 || K < 1) {
            return 0;
        }
        // monster在经历K次打击后所有可能的掉血情况是
        long all = (long) Math.pow(M + 1, K);
        long kill = process(K, M, N);
        return (double) kill / (double) all;
    }

    //怪兽还剩 hp 点血，每次的伤害在[0……M]范围上，还有 times 次可以砍，返回砍死的情况数。
    public static long process(int times, int M, int hp) {
        // 情况一：已经没有被砍的次数了，这个时候，血量如果正好是小于等于0的值， 说明怪兽已经被砍死一次
        // 否则怪兽不可被砍死
        if (times == 0) {
            return hp <= 0 ? 1 : 0;
        }
        // 情况二：怪兽已经死了，但是还可以砍
        // 此时，所有的砍法都满足条件，所以情况就是(long) Math.pow(M + 1, times)
        if (hp <= 0) {
            return (long) Math.pow(M + 1, times);
        }
        long ways = 0;
        for (int i = 0; i <= M; i++) {
            ways += process(times - 1, M, hp - i);
        }
        return ways;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

动态规划（未做枚举优化）

根据上述暴力递归函数可以得知，递归函数的可变参数有两个，分别是 times 和 hp，且变化范围是固定的，可以定义一个二维数组 dp，表示所有的递归过程解

long[][] dp = new long[K + 1][N + 1];
1

dp[times][hp] 就表示递归函数long process(int times, int M, int hp)的含义，即：怪兽还剩 hp 点血，每次的伤害在[0……M]范围上，还有 times 次可以砍，砍死的情况数有多少。

根据 base case, 可知

dp[0][0] = 1;
1

且

dp[times][0] = (long) Math.pow(M + 1, times)
1

接下来就是普遍位置，根据上述暴力递归函数可知：process(times, M, hp)依赖process(times - 1, M, hp - i)

即dp[times][hp]依赖dp[times-1][hp-i]位置，如下图所示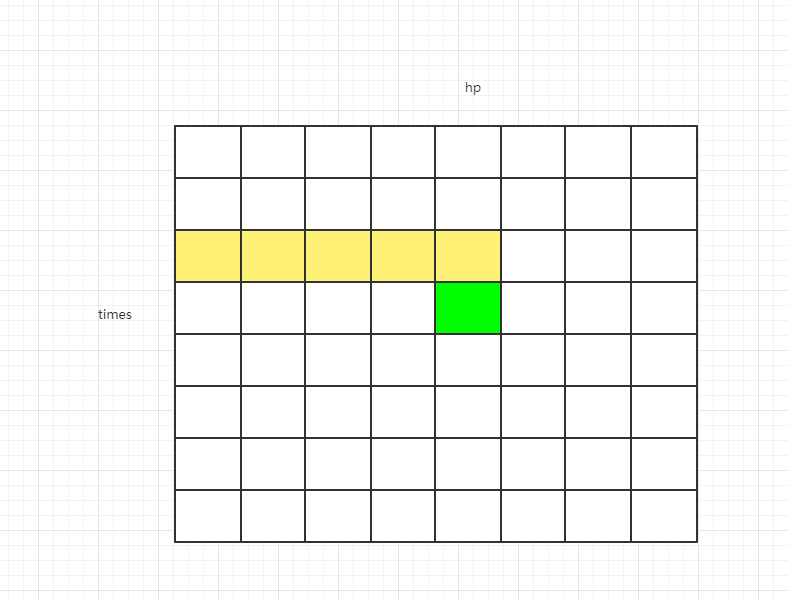

图中绿色部分的格子依赖黄色部分的格子，

代码如下，

for (int times = 1; times <= K; times++) {
    dp[times][0] = (long) Math.pow(M + 1, times);
    for (int hp = 1; hp <= N; hp++) {
        long ways = 0;
        for (int i = 0; i <= M; i++) {
            if (hp - i >= 0) {
                ways += dp[times - 1][hp - i];
            } else {
                ways += (long) Math.pow(M + 1, times - 1);
            }
        }
        dp[times][hp] = ways;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

完整代码如下

public class Code_KillMonster {
    public static double dp1(int N, int M, int K) {
        if (N < 1 || M < 1 || K < 1) {
            return 0;
        }
        long all = (long) Math.pow(M + 1, K);
        long[][] dp = new long[K + 1][N + 1];
        dp[0][0] = 1;
        for (int times = 1; times <= K; times++) {
            dp[times][0] = (long) Math.pow(M + 1, times);
            for (int hp = 1; hp <= N; hp++) {
                long ways = 0;
                for (int i = 0; i <= M; i++) {
                    if (hp - i >= 0) {
                        ways += dp[times - 1][hp - i];
                    } else {
                        ways += (long) Math.pow(M + 1, times - 1);
                    }
                }
                dp[times][hp] = ways;
            }
        }
        long kill = dp[K][N];
        return (double) ((double) kill / (double) all);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

动态规划（枚举优化）

上述动态规划解法中的第三个循环可以优化，再一次看下依赖关系图

当我们得到绿色格子，即dp[times][hp]位置的值以后，如果要求dp[times+1][hp]位置的时候，即如下 target 位置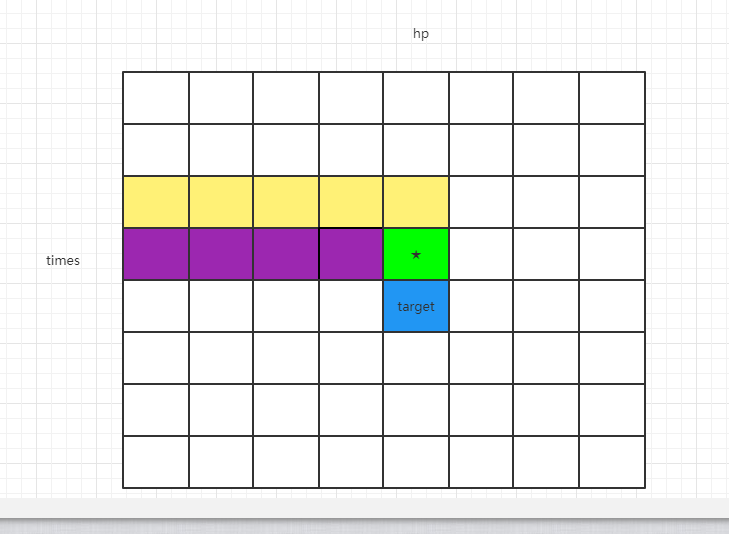

可以考虑 G 和 H 两个位置

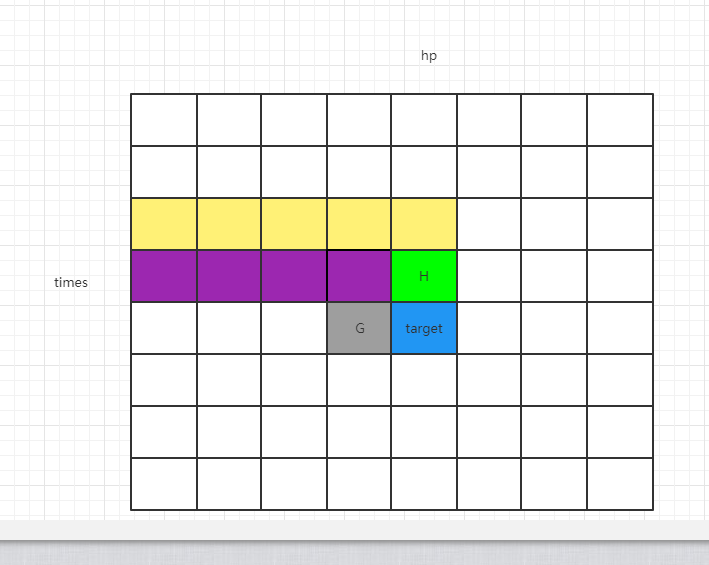
因为 G 位置求的时候，紫色部分格子已经求过了，补上一个 H 位置，就可以把 target 求出来，省略了枚举行为。

完整代码如下

public class Code_KillMonster {
    public static double dp2(int N, int M, int K) {
        if (N < 1 || M < 1 || K < 1) {
            return 0;
        }
        long all = (long) Math.pow(M + 1, K);
        long[][] dp = new long[K + 1][N + 1];
        dp[0][0] = 1;
        for (int times = 1; times <= K; times++) {
            dp[times][0] = (long) Math.pow(M + 1, times);
            for (int hp = 1; hp <= N; hp++) {
                dp[times][hp] = dp[times][hp - 1] + dp[times - 1][hp];
                if (hp - 1 - M >= 0) {
                    dp[times][hp] -= dp[times - 1][hp - 1 - M];
                } else {
                    dp[times][hp] -= Math.pow(M + 1, times - 1);
                }
            }
        }
        long kill = dp[K][N];
        return (double) ((double) kill / (double) all);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

更多

算法和数据结构笔记