第二章：整数二分与浮点数二分（极限思想）

二分的数学思想：

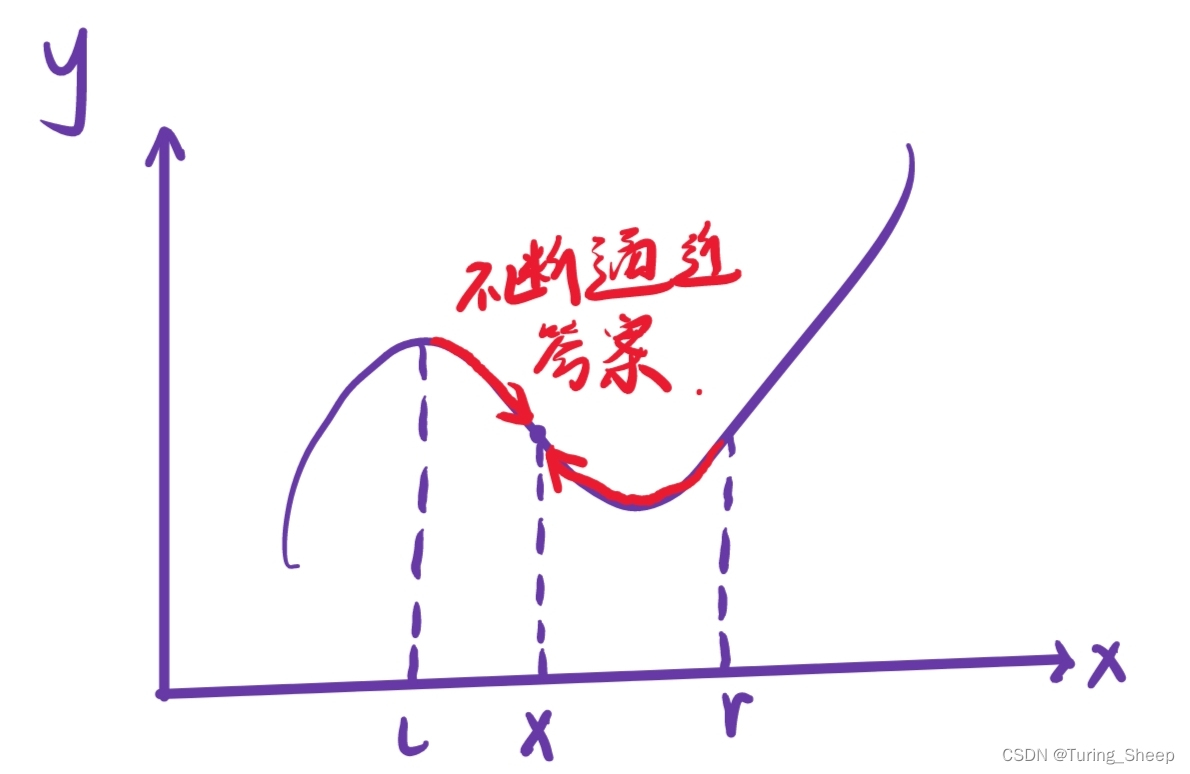
二分的数学思想其实就是极限，我们通过取中点的方式，不断地缩小答案所在的区间，让这个区间不断地逼近答案，类似于我们在高数中所学的极限：

一、整数二分

1、思路

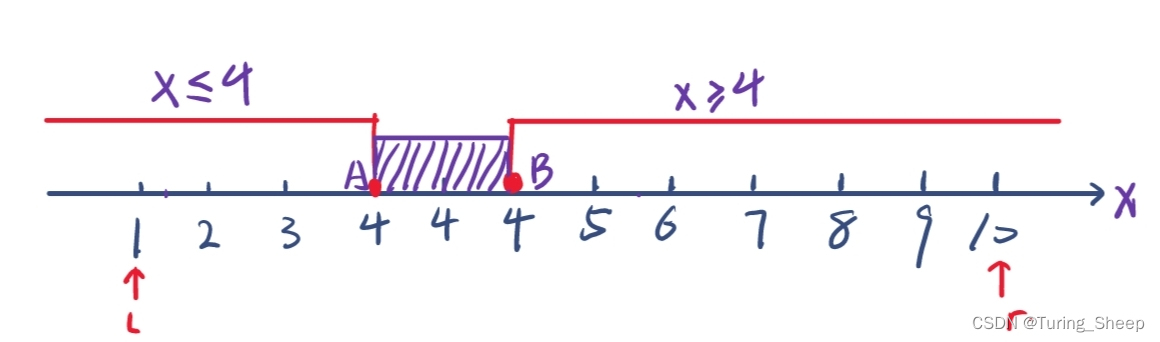
我们假设想要寻找上述数轴中的左右边界。

我们先看左边界中的A点，不看B点。我们仔细观察一下A点处符合的性质。

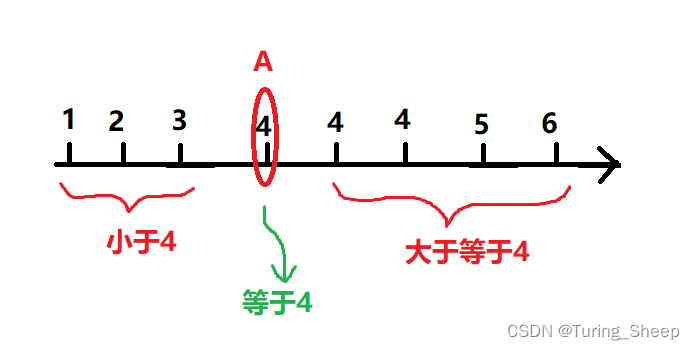
根据上图中的性质，我们就可以开始写二分了。

根据刚刚的描述二分是一个不断逼近地过程，可以理解为两侧端点不断靠近的过程。

将左端点的下标设为$l$，右端点下标设为$r$，中间点的下标设为$mid$，$mid=(l+r)/2$

令$l=0$,$r=n-1$

如果$mid$处所对的元素值小于$4$，说明我们的端点$A$一定不在$mid$点处，又因为这个序列是单调递增的，所以$mid$左侧的数字都是小于$mid$所对的值的。也就是说$mid$左侧的数字都是小于$4$的，而我们的$A$处是等于$4$的。

那么知道这个有什么用呢？

这就说明$mid$的左侧包括$mid$都不可能是$A$点，所以我们可以让$l=mid+1$。

如果$mid$处所对的值是大于等于$4$的，说明$mid$右侧的值也一定是大于等于$4$的。

而$mid$处的值也是等于$4$的，也就是说$mid$处可能是答案，此时我们考虑一下$mid$右侧的情况。

如果$mid$右侧的值都比$mid$大，那么$mid$右侧的树也不可能是答案，因为他们都大于$4$。

如果$mid$右侧还有等于$4$的值，但这些不可能是答案，因为我们找的是区间的左端点，如果$mid$处是$4$，那么$mid$右侧的$4$肯定不是左端点。

通过上面对$mid$右侧的讨论，我们发现$mid$右侧都不可能是答案，但是$mid$处有可能是答案。所以我们可以扔掉$mid$右侧的数，即直接让$r=mid$。

通过一轮的比较，我们发现两端的端点再向中间靠拢。

因此我们只需要重复上面的比较，当左端点和右端点合并到一起的时候，那个点就是区间的左端点$A$。

接着我们考虑区间的右端点。

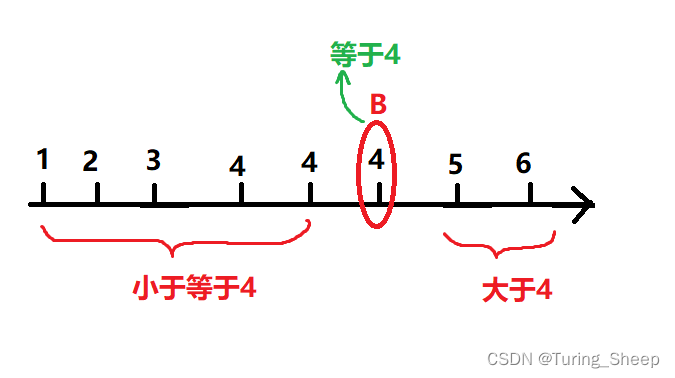
右端点就是$B$点，还是和刚才的思路一样，B点一定在这个数轴上，所以我们让左端点$l$指向起点$0$，右端点$r$指向最后一个元素下标的$n-1$。

我们求出一个中点$mid$，

如果$mid$处所对的值是大于4的。

那么$mid$处肯定不符合条件，由于这个序列是单调递增的，所以$mid$右侧的数字也一定是大于4的，即不符合条件的。因此，我们可以直接扔掉$mid$所对的点和它右面的点。即$r=mid-1$

接着如果$mid$处所对的值是小于等于4的。

那么$mid$处有可能是答案，然后我们考虑$mid$左侧的值。

如果$mid$左侧的值都是小于4的，那么$mid$左侧的数字肯定不是答案，可以直接扔掉，如果$mid$左侧存在等于4的数，这些4也不可能是答案，因为我们找的是右端点，mid在这些4的右面。所以也可以扔掉。

因此如果$mid$处所对的值，我们可以直接扔掉$mid$左侧的数，但是需要保留$mid$，即$l=mid$

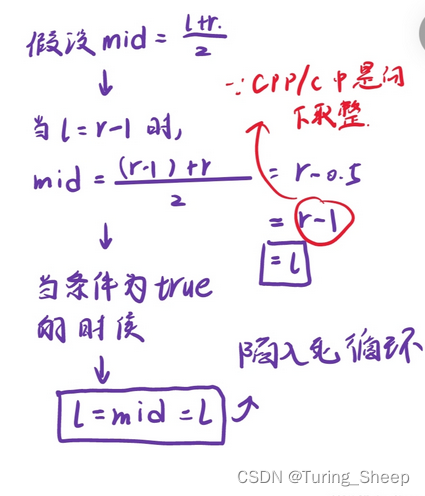
但是我们找左端点的时候，$mid=(l+r)/2$，而现在由于除法是下取整，所以mid的算法是$(l+r+1)/2$。

为什么呢？

我们看下面这个极端的例子：

2、模板

我们以下面的题目为例：

上述题目来自acwing网站

C++版

#include
using namespace std;
const int N=1e6+10;
int arr[N];

int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++)scanf("%d",&arr[i]);
    while(m--)
    {
        //输入要查找的数字
        int f=0;
        cin>>f;
        //开始二分：
        //寻找左边界
        int l=0,r=n-1;
        int mid;
        while(l<r)
        {
            mid=(l+r)>>1;
            if(arr[mid]>=f)r=mid;
            else l=mid+1;
            
        }
        if(arr[l]!=f)cout<<"-1 -1"<<endl;
        else
        {
            cout<<l<<" ";
            //寻找右边界
            l=0,r=n-1;
           
            while(l<r)
            {

                mid=(l+r+1)>>1;
                if(arr[mid]<=f)l=mid;
                else r=mid-1;
            }
            cout<<r<<endl;
        }
    }
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

二、浮点数二分

1、思路：

假设我们想求一个数字的立方根，并且要保留6位小数，那么必定存在一个范围都是满足这个答案的，因为通过四舍五入后，这个范围的答案都是正确的。此时我们就可以利用浮点数二分。

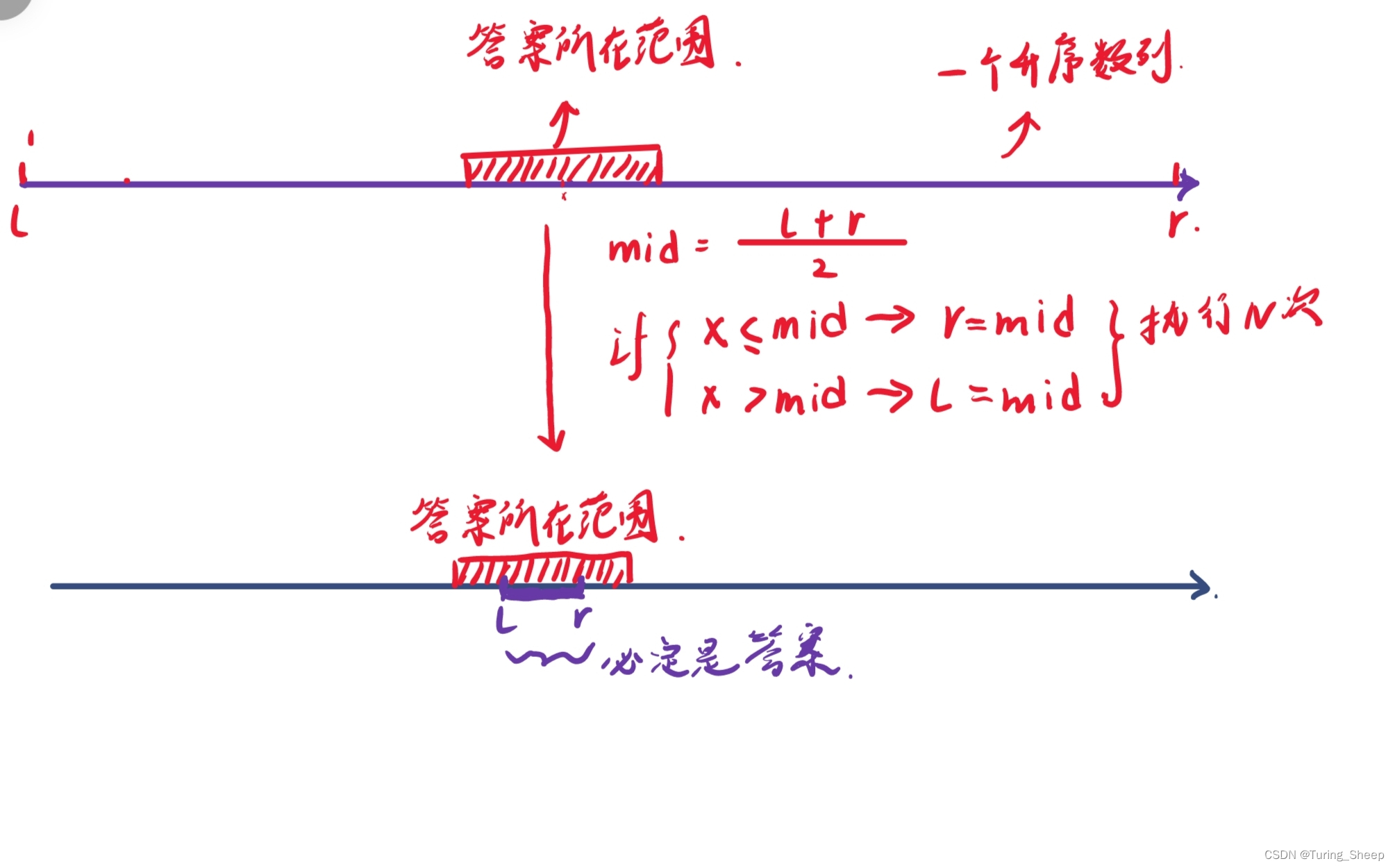
所以浮点数二分的思想就是，我们让l到r所组成的区间全部落在答案所在的范围内。此时我们在输出答案即可。

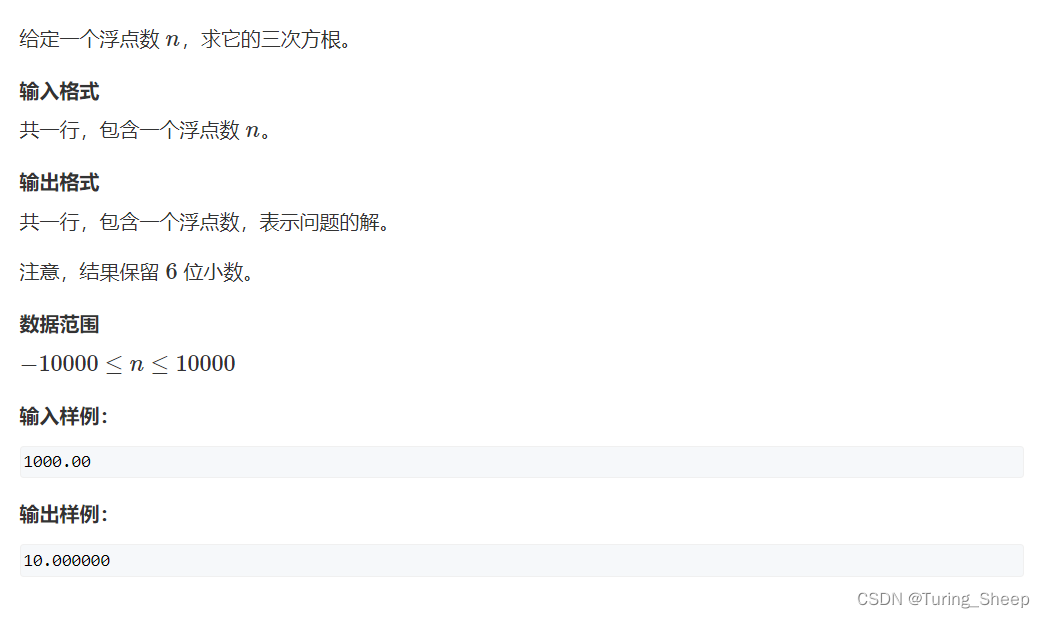
来自acwing。

2、代码：

C++版

#include
using namespace std;

double x;
double l=-10000.00;
double r=10000.00;
int main()
{
    cin>>x;
    while(r-l>1e-10)
    {
        double mid=(r+l)/2;
        if(mid*mid*mid>=x)r=mid;
        else l=mid;
    }
    printf("%.6lf",l);;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

C

#include

double x;
double l=-10000.00;
double r=10000.00;
int main()
{
    scanf("%lf",&x);
    while(r-l>1e-10)
    {
        double mid=(r+l)/2;
        if(mid*mid*mid>=x)r=mid;
        else l=mid;
    }
    printf("%.6lf",l);;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17