2014软专 P117

第二题

思路

1、两点间距离公式

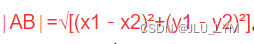
double getDist(point a, point b) {//求两点间距离公式
	return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
1
2
3

2、计算机中常常给三点坐标，要求三角形面积
<1>求出三条边长度(用上一条中的公式)
<2>求出p

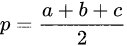
<3>利用“海伦公式”即

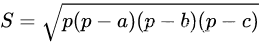
求出三角形面积

double getArea(point a, point b, point c) {//海伦公式求面积
	double ab = getDist(a, b);
	double ac = getDist(a, c);
	double bc = getDist(b, c);
	double p = (double)(ab + ac + bc) / 2;
	return sqrt(p*(p - ab)*(p - ac)*(p - bc));
}

1
2
3
4
5
6
7
8

3、如何判定一个点是否在三角形内部：
看这个点能否三分三角形面积，即：Sabc==Sabd+Sacd+Sbcd是否成立

4、浮点数判断是否相等
用两个浮点数取差值，再取绝对值，和给出的精度比较，小于即是认为二者相等

注意数学公式的记忆！

代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef struct point {
	int x;
	int y;
}point;
double getDist(point a, point b) {//求两点间距离公式
	return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
double getArea(point a, point b, point c) {//海伦公式求面积
	double ab = getDist(a, b);
	double ac = getDist(a, c);
	double bc = getDist(b, c);
	double p = (double)(ab + ac + bc) / 2;
	return sqrt(p*(p - ab)*(p - ac)*(p - bc));
}
void function_two() {
	point a, b, c, d;
	cin >> a.x >> a.y;
	cin >> b.x >> b.y;
	cin >> c.x >> c.y;
	cin >> d.x >> d.y;
	double Sabc = getArea(a, b, c);
	double Sabd = getArea(a, b, d);
	double Sacd = getArea(a, c, d);
	double Sbcd = getArea(b, c, d);
	if (fabs(Sabc - Sabd - Sacd - Sbcd) < 1e-8) {//浮点数判等方法，不等号右侧为精度，具体看题目要求
		cout << "true";
		return;
	}
	cout << "false";
	return;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

第三题

思路

就是模仿我们人类在计算时候的过程

注意：
1、最后一步，需要清空进位中的数字，千万别忘了，将之放到新数的最高位
2、需要知道每次计算后新的数放在何处。eg: a*b j标识a的某一位原来所在位数，i标识b的第几位与之相乘，也同时代表了新数储存时候偏移量(实在不懂就自己写一个乘法运算，自己看)，所以存储位置是i+j

代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
void function_three(int a, int b) {
	//处理数据格式
	int a1[100];
	int n1 = 0;
	int b1[100];
	int n2 = 0;

	int ans[100] = {};

	while (a != 0) {
		a1[n1++] = a % 10;
		a /= 10;
	}
	while (b != 0) {
		b1[n2++] = b % 10;
		b /= 10;
	}

	//开始算法  A * B(就是模拟手动计算过程)
	for (int i = 0; i < n2; i++) {//枚举B中的每一位
		int aOne = 0;//记录两次进位
		int aTwo = 0;
		for (int j = 0; j <= n1; j++) {//枚举A中的每一位
			if (j == n1) {
				ans[i + j] = aOne + aTwo;//把进位中的数再加上即可，防止有遗漏
			}
			else {
				int tmp1 = a1[j] * b1[i] + aOne;//两个目标数相乘
				aOne = tmp1 / 10;//获取第一次进位，用于下一次乘法
				int tmp2 = (tmp1 % 10) + ans[i + j] + aTwo;//准备加入进ans数组
				aTwo = tmp2 / 10;//获取加入时候的进位，用于下一次加入使用
				ans[i + j] = tmp2 % 10;//更新相应位置数据，i+j这个就是模拟咱们做乘法的模式(A中原本的位数+B中偏移的位数)
			}
		}
	}

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

第四题

思路和第二题一样，就是最后枚举所有三个点的组合的时候，abc bca cab这些都代表了一个三角形，只需要算一次即可，所以去重

typedef struct point {
	int x;
	int y;
};
double getDist(point a, point b) {
	return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
double getArea(point a, point b, point c) {
	double ab = getDist(a, b);
	double ac = getDist(a, c);
	double bc = getDist(b, c);
	double p = (double)(ab + ac + bc) / 2;
	return sqrt(p*(p - ab)*(p - ac)*(p - bc));
}
void function_four() {//暴力枚举即可
	point item[100];
	for (int i = 0; i < 100; i++) {
		cin >> item[i].x >> item[i].y;
	}
	double ans = -1;
	for (int i = 0; i < 100; i++) {//枚举时候去重,重复的三个点毫无意义
		for (int j = i + 1; j < 100; j++) {
			for (int k = i + 2; k < 100; k++) {
				double s = getArea(item[i], item[j], item[k]);
				ans = max(ans, s);
			}
		}
	}
	cout << ans;
	return;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

第六题

（1）

思路

正常层序遍历，就是从上到下，（不论“从左到右”还是“从右到左”，就是入队顺序变一下，很简单），但我现在想从下到上，那就把基础代码得到的结果反过来就行

代码

class Solution {
public:
	vector<vector<int>> levelOrderBottom(TreeNode* root) {
		if (root == nullptr) {
			return {};
		}
		vector<vector<int>> ans;
		queue<TreeNode*> help;
		int size = 1;
		help.push(root);

		while (!help.empty()) {
			int tmp_size = 0;
			vector<int> tmp;
			for (int i = 0; i < size; i++) {
				TreeNode* item = help.front();
				help.pop();
				tmp.push_back(item->val);
				if (item->right != nullptr) {//先入右子节点
					tmp_size++;
					help.push(item->right);
				}
				if (item->left != nullptr) {
					tmp_size++;
					help.push(item->left);
				}
			}
			size = tmp_size;
			ans.push_back(tmp);
		}

		reverse(ans.begin(), ans.end());//要从最底下开始，那就倒过来
		return ans;
	}
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

（2）

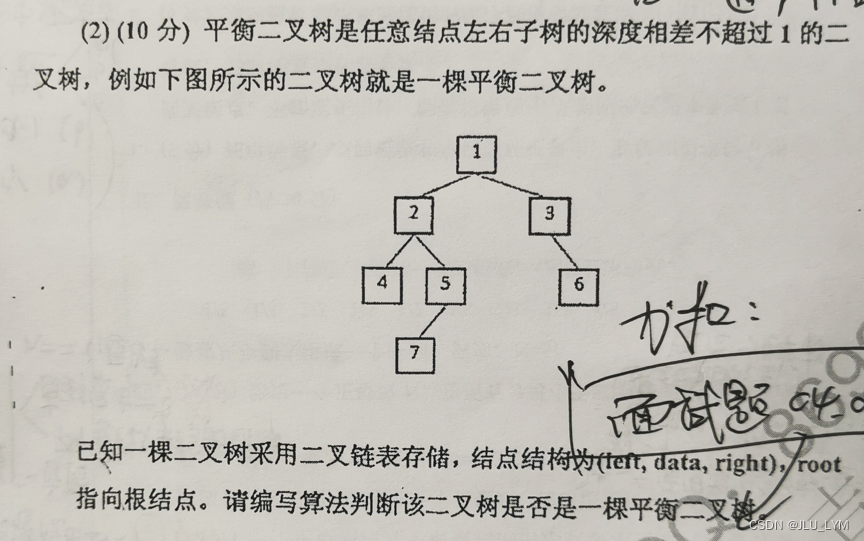
详细代码模板见：
第五章–二叉树 板子