-
基于离散、连续、线性和非线性模型进行模型预测(MPC)控制(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
目录
💥1 概述
模型预测控制MPC(Model Predictive Control)是70年代末发展起来的新型计算机控制算法。经过多年的理论研究和应用实践,MPC在算法改进和理论分析方面都有很大发展。它的典型算法有三种:模型算法控制MAC(Model Algorithm Control),动态矩阵控制DMC(Dynamic Matrix Control)和广义预测控制GPC(Generalized Predictive Control) [1.2l。目前,MPC在石油、化工、冶金等多个工业部门都得到了成功的应用。与此同时,不少国外软件公司已经推出了各具特色的MPC商业化应用软件。现在人们已普遍认为MPC是一类最具实用性,有着广泛应用前景的先进控制策略[3]。
模型预测控制 (MPC) 可预测和优化未来时间范围内的时变过程。此控制包接受线性或非线性模型。利用APOPT、IPOPT等大规模非线性规划求解器,解决数据调和、移动视界估计、实时优化、动态仿真、非线性MPC问题[4]。
📚2 运行结果

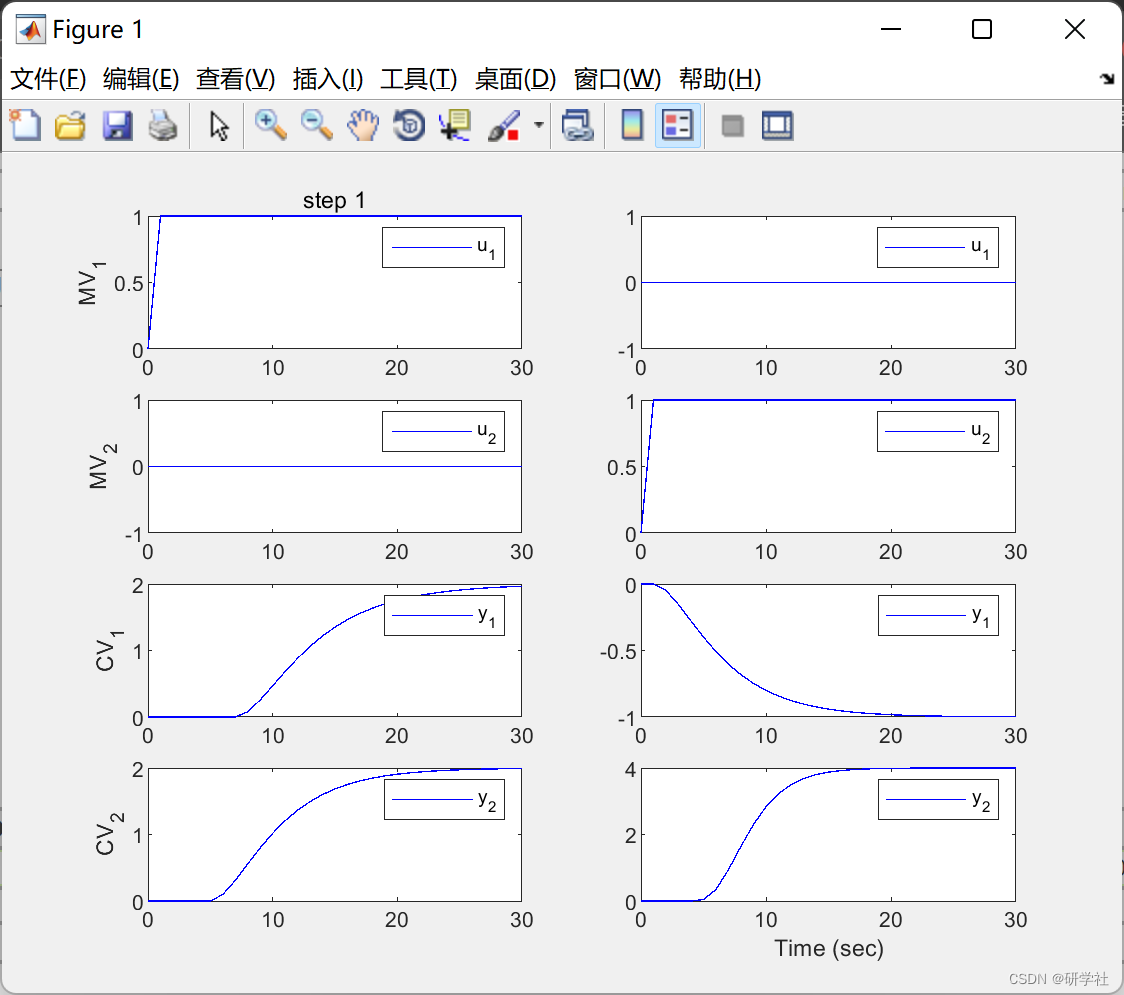 部分代码:
部分代码:% define 2 x 2 control matrix in s-domain (continuous)
G11 = 2/((5*s+1)*(2*s+1))*exp(-6*s);
G12 = -1/((4*s+1)*(2*s+1));
G21 = 2/((4*s+1)*(2*s+1))*exp(-4*s);
G22 = 4/((2*s+1)*(s+1)^3)*exp(-3*s);% overall transfer function
Gc = [G11 G12;...
G21 G22];% get step response
figure(1)
step(Gc)% convert to discrete form with 1 second sampling (z-domain)
Gd = c2d(Gc,1);
hold on
step(Gd)% convert to state space
sys = absorbDelay(ss(Gd));
step(sys)% extract A, B, C, D matrices in sparse form
[n,m] = size(sys.B);
[p,m] = size(sys.D);[ai,aj,av] = find(sparse(sys.A));
a = [ai,aj,av]';
[bi,bj,bv] = find(sparse(sys.B));
b = [bi,bj,bv]';
[ci,cj,cv] = find(sparse(sys.C));
c = [ci,cj,cv]';
[di,dj,dv] = find(sparse(sys.D));
d = [di,dj,dv]';
if(size(d,2)==0),
d = [1,1,0]';
endfid = fopen('lti.apm','w');
fprintf( fid,'\n');
fprintf( fid,'Objects \n');
fprintf( fid,' sys = lti\n');
fprintf( fid,'End Objects \n');
fprintf( fid,'\n');
fprintf( fid,'Connections\n');
fprintf( fid,' u[1:%d] = sys.u[1:%d]\n',m,m);
fprintf( fid,' x[1:%d] = sys.x[1:%d]\n',n,n);
fprintf( fid,' y[1:%d] = sys.y[1:%d]\n',p,p);
fprintf( fid,'End Connections\n');
fprintf( fid,'\n');
fprintf( fid,'Model \n');
fprintf( fid,' Parameters \n');
fprintf( fid,' u[1:%d] = 0\n',m);
fprintf( fid,' End Parameters \n');
fprintf( fid,'\n');
fprintf( fid,' Variables \n');
fprintf( fid,' x[1:%d] = 0\n',n);
fprintf( fid,' y[1:%d] = 0\n',p);
fprintf( fid,' End Variables \n');
fprintf( fid,'\n');
fprintf( fid,' Equations \n');
fprintf( fid,' ! add any additional equations here \n');
fprintf( fid,' End Equations \n');
fprintf( fid,'End Model \n');
fprintf( fid,'\n');
fprintf( fid,'! dimensions\n');
fprintf( fid,'! (nx1) = (nxn)*(nx1) + (nxm)*(mx1)\n');
fprintf( fid,'! (px1) = (pxn)*(nx1) + (pxm)*(mx1)\n');
fprintf( fid,'!\n');
fprintf( fid,'! discrete form\n');
fprintf( fid,'! x[k+1] = A * x[k] + B * u[k]\n');
fprintf( fid,'! y[k] = C * x[k] + D * u[k]\n');🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]万鹏. 基于模型预测控制(MPC)车道保持系统的研究[D].安徽工程大学,2022.DOI:10.27763/d.cnki.gahgc.2022.000005.
[2]哈迪(DHAIF ALLAH HADI). 基于模型预测控制(MPC)的光伏发电智能控制研究[D].华北电力大学(北京),2020.DOI:10.27140/d.cnki.ghbbu.2020.001065.
[3]John Hedengren (2022). Model Predictive Control.
[4]隋丹,冯乐,陈蓓.模型预测控制(MPC)在飞机自动着陆系统中的应用[J].航空计算技术,2003(03):23-26.
🌈4 Matlab代码实现
-
相关阅读:
Deep Learning-深度学习(二)
markdown 如何书写 arg min max公式
数字化转型总体需求
docker应用篇(9):搭建DNS服务器
构建可扩展的应用:六边形架构详解与实践
Unittest(单元测试)
window 服务器 短文件名漏洞处理
再见SpringCloud,这个架构挺猛,甚至干掉Dubbo
Pytorch2.0发布了,向下兼容,加一句代码,性能翻番
ElementUI浅尝辄止37:Select 选择器
- 原文地址:https://blog.csdn.net/weixin_46039719/article/details/127825983