保边滤波之引导滤波与领域转换滤波

（1）引导滤波

局部窗口内输出图像O和引导图像G成线性关系Oi=akGi+bk, ∀i∈Ωk
假设输出图像O和输入图像I之间的关系为Oi=Ii−ni，噪声最小即最小化ni，即

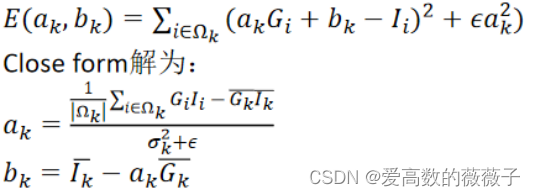
每个像素点i包含于多个窗口Ωk，每个窗口都会得到一个a、b值，对所有窗口得到的像素点i的a、b值做平均,a*G+b=O，得到输出图像O。
引导滤波中的半径r、规整项参数ϵ与双边滤波中的σs和σr^2
r越大，图像越模糊，ϵ越大，图像越模糊 （约束ak的平方不能太大）ak越小，导致akGi+bk-Ii差得很远，模糊。
引导滤波的滤波核：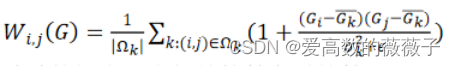

Gi和Gk在均值的同一边，相似度高；在均值的不同边，相似度低。高相似度的值进行加权平均，起到保边的作用。

对比：
相比于双边滤波器，引导滤波可以有效去除梯度反转（Gradient reversal）
引导滤波器和双边局部滤波器都会产生halo伪像
引导滤波器没有spatial核，所以没有双边滤波器稳定，它只管颜色相似，不管位置。

改进效果：
根据图片内容去调整模糊程度ϵ：WGIF，GGIF
边缘区域ϵ小一些
平坦区域ϵ大一些

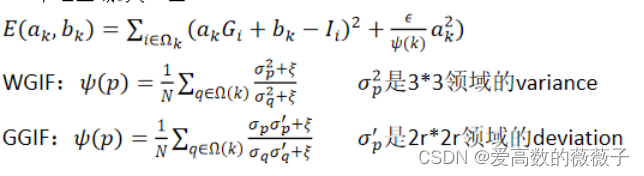
越平坦，根据GGIF，越小；越边缘，根据WGIF，越大
进一步提升速度：降采样。图片降采样，在降采样的图片上算a和b，再给a,b求均值，再给a,b直接上采样，再按公式算。

（2）领域转换滤波

保边滤波结果=仿射矩阵输入图像->O=AI
如果能够将图像（三维数据点）数据映射到二维数据点，并且能够保证仿射矩阵不变，就能提高滤波效率，然而三维到二维的变换是不存在的，二维（一行或者一列图像）到一维的变换是存在的

将二维上曲线的距离拉成一维上两个定义域的距离：
采用一范式，距离：|x1-x2|+|y1-y2|

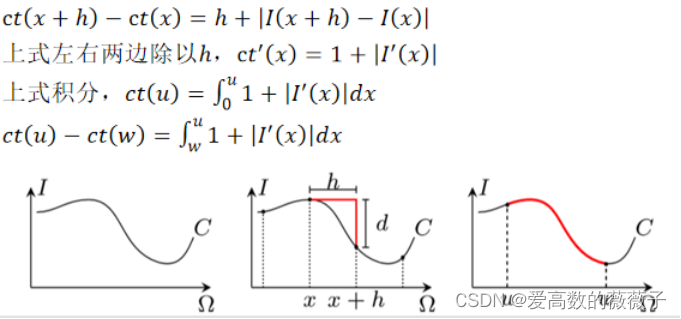
一维领域转换保边滤波：

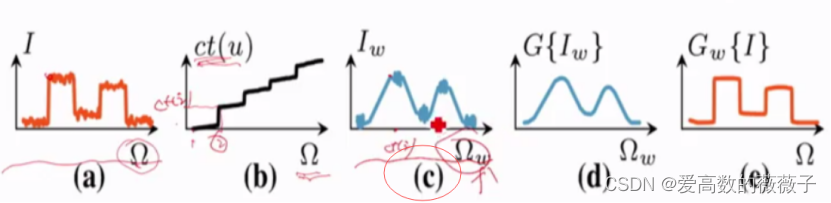
图C什么意思不太懂
在图像上，通常计算相似度的时候会考虑给定义域(Domain)和值域(Range)不同的权重σ，而在一维数据中，我们只有一个参数了，假设转换后的滤波核参数是σH=σs
转换时嵌入：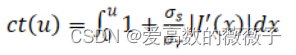
（谁更重要加个权）

前面讲了图像的一行滤波，然而图像是二维的，在二维图像进行领域转换滤波，作者提出要迭代进行行滤波、列滤波，每个行滤波跟着一个列滤波。每次迭代降低滤波参数σH（以此去除条带状伪像）

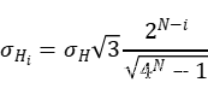
第i轮的滤波参数
作者提出了三种一维上的滤波方法：NC IC RF
领域转换后并不是均匀采样。NC的原理是直接把缺失的点当0算，IC的原理是把缺失的点插值，按均匀采样在转换后的Domain里面做Box filter，r=√3σH

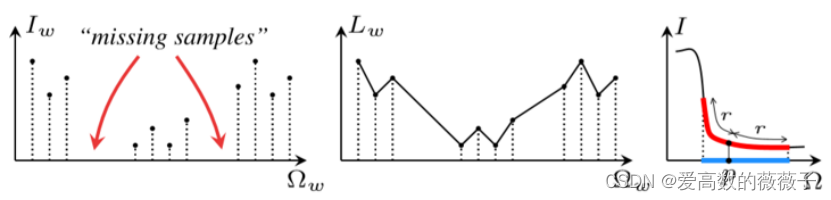
NC和IC原理图
RF递归滤波公式：

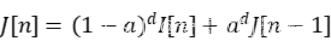
I代表原图像，J代表滤波输出

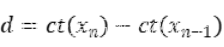
两点之间的梯度

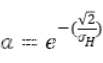
定值在0到1
假设d很大，导致两点之间差异大梯度大，是个非常明显的边界，前面一点对它的影响很小。