用于回归问题的异常鲁棒极限学习机（ORELM）（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

文献来源：

极限学习机（ELM）作为机器学习中最有用的技术之一，因其独特的极快学习能力而受到广泛关注。特别是，人们普遍认为ELM在执行令人满意的结果的同时具有速度优势。但是，异常值的存在可能会导致不可靠的ELM模型。在本文中，我们的研究解决了回归问题中ELM的异常鲁棒性。基于异常值的稀疏性特征，本文提出了一种异常鲁棒ELM，其中1-范数损失函数用于增强鲁棒性。特别是，采用快速准确的增强拉格朗日乘子方法，保证了有效性和效率。通过函数逼近实验和一些实际应用，所提方法不仅保持了原始ELM的优势，而且在处理异常值数据方面表现出显著且稳定的准确性。 

📚2 运行结果

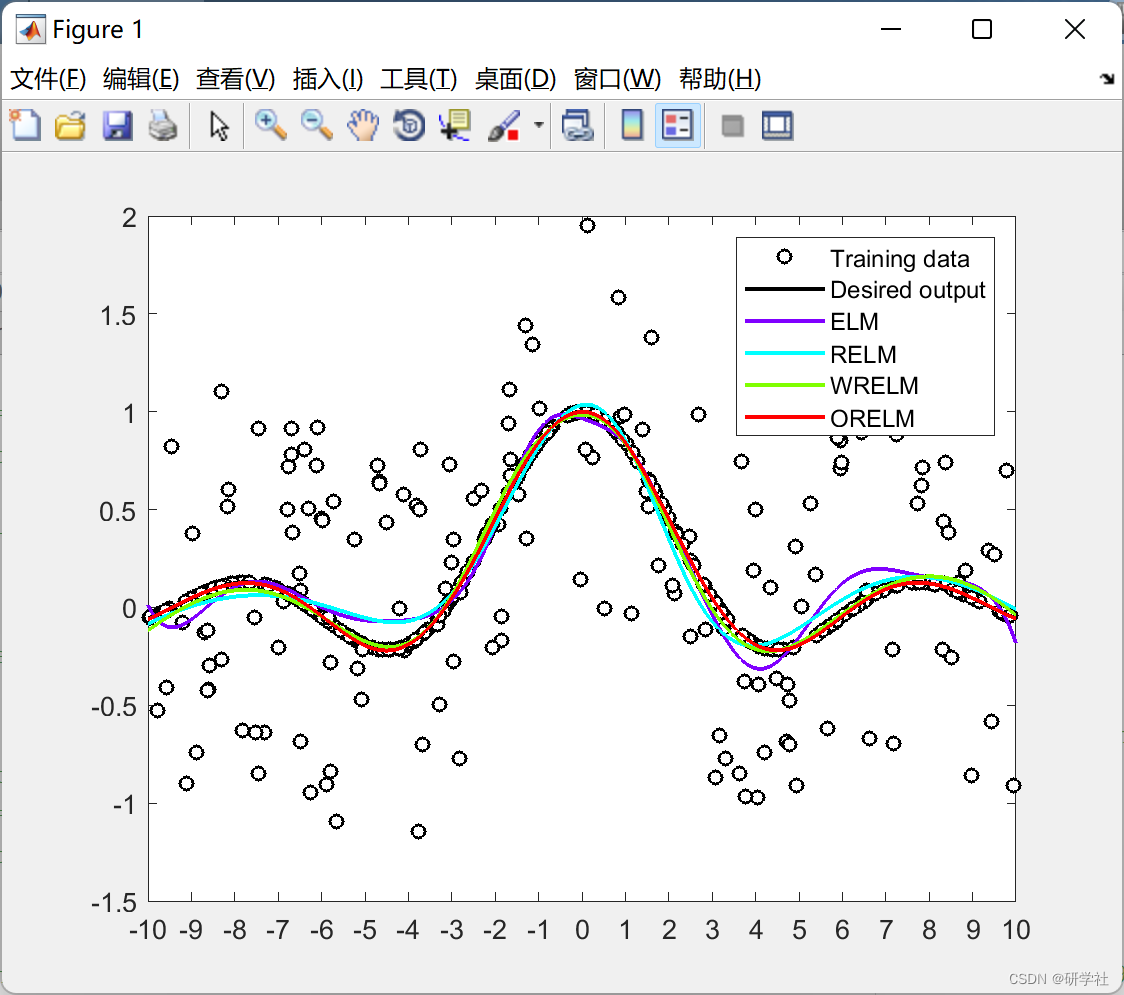
 部分代码：

nn.hiddensize     = 20;
method            = {'ELM','RELM','WRELM','ORELM'};
type              = {'regression','classification'};
nn.type           = type{1};
nn.inputsize      = size(traindata,1);
nn.activefunction = 's';
nn.orthogonal     = false;
fprintf('            method             |  Training Acc.  |    Testing Acc.   |   Training Time \n');

%%%------------------------------------------------------------------------
%%%   ELM / Original ELM
%%%------------------------------------------------------------------------

nn.method         = method{1};
nn                = elm_initialization(nn);
[nn, acc_train]   = elm_train(traindata, trainlabel, nn);
[nn1, acc_test]   = elm_test(testdata, testlabel, nn);
fprintf('      %19s      |      %.3f      |      %.5f      |      %.5f      \n',nn.method,acc_train,acc_test,nn.time_train);

%%%------------------------------------------------------------------------
%%%   RELM / Regularized ELM
%%%------------------------------------------------------------------------

nn.method         = method{2};
nn                = elm_initialization(nn);
nn.C              = 0.0001;
[nn, acc_train]   = elm_train(traindata, trainlabel, nn);
[nn2, acc_test]   = elm_test(testdata, testlabel, nn);
fprintf('      %19s      |      %.3f      |      %.5f      |      %.5f      \n',nn.method,acc_train,acc_test,nn.time_train);

%%%------------------------------------------------------------------------
%%%   WRELM / Weighted Regularized ELM
%%%------------------------------------------------------------------------

nn.method         = method{3};
nn.wfun           = '1';
nn.scale_method   = 1;
nn                = elm_initialization(nn);
nn.C              = 2^(-20);
[nn, acc_train]   = elm_train(traindata, trainlabel, nn);
[nn3, acc_test]   = elm_test(testdata, testlabel, nn);
fprintf('      %19s      |      %.3f      |      %.5f      |      %.5f      \n',nn.method,acc_train,acc_test,nn.time_train);

%%%------------------------------------------------------------------------
%%%   ORELM / Outlier-Robust ELM
%%%------------------------------------------------------------------------

nn.method         = method{4};
nn                = elm_initialization(nn);
nn.C              = 2^(-40);
[nn, acc_train]   = elm_train(traindata, trainlabel, nn);
[nn4, acc_test]   = elm_test(testdata, testlabel, nn);
fprintf('      %19s      |      %.3f      |      %.5f      |      %.5f      \n',nn.method,acc_train,acc_test,nn.time_train);

%%%------------------------------------------------------------------------
%%%   Plot
%%%------------------------------------------------------------------------

figure(1);
plot(traindata,trainlabel,'o','MarkerSize',5,'MarkerFaceColor','w','MarkerEdgeColor','k','linewidth',1);
hold on;
plot(testdata,testlabel,'k','linewidth',1.5);

nb_topics = 4;
cmap      = hsv(nb_topics);
cmap      = flip(cmap,1);
Acc_test  = zeros(1,nb_topics);
for i = 1:nb_topics
    %hold on;
    Acc_test(i) = eval(['nn',num2str(i),'.acc_test']);
    plot(testdata,eval(['nn',num2str(i),'.testlabel']),'color',cmap(i,:),'linewidth',1.5);
end
axis([-10,10,-1.5,2]);
set(gca,'XTick',-10:1:10)

legend1 = legend([{'Training data'},{'Desired output'},method]);

name = 'fig1';
print('-depsc','-painters',[name,'.eps']);

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1] "Zhang K, Luo M. Outlier-robust extreme learning machine for regression problems[J]. Neurocomputing, 2015, 151: 1519-1527.".

🌈4 Matlab代码实现