6234. 最小公倍数为 K 的子数组数目

题目

子数组 是数组中一个连续非空的元素序列。

数组的最小公倍数 是可被所有数组元素整除的最小正整数。

 

示例 1 ：

输入：nums = [3,6,2,7,1], k = 6
输出：4
解释：以 6 为最小公倍数的子数组是：
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]

示例 2 ：

输入：nums = [3], k = 2
输出：0
解释：不存在以 2 为最小公倍数的子数组。

 

提示：

• 1 <= nums.length <= 1000
• 1 <= nums[i], k <= 1000

解析

题目有提到两个关键字，统计子数组 和 最小公倍数 。

数学概念及其代码

公倍数：两个或多个整数公有的倍数叫做它们的公倍数，其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。
最大公约数 最大公约数,最大公约数,也称最大公因数、最大公因子,指两个或多个整数共有约数中最大的一个。

使用代码求出两个数的最小公倍数既LCM，LCM是两数的乘积除以他们的最大公约数。

private int gcd(int a, int b) {
	if (b == 0) return a;
	return gcd(b, a % b);
}

private int lcm(int a, int b) {
	return a * b / gcd(a, b);
}
1
2
3
4
5
6
7
8

子数组

1. 三层循环统计子数组数量

这题解毫无疑问会超时，数据量1000，最坏的情况是n^3。

class Solution {
	private int gcd(int a, int b) {
        if (b == 0) return a;
        return gcd(b, a % b);
    }

    private int lcm(int a, int b) {
        return a * b / gcd(a, b);
    }

	public int subarrayLCM(int[] nums, int k) {
	    int ans = 0;
	    for (int i = 0; i < nums.length; i++) {
	        for (int j = i; j < nums.length; j++) {
	            int res = 1;
	            for (int l = i; l <= j; l++) {
	                res = lcm(nums[l], res);
	            }
	            if (res == k) ans++;
	        }
	    }
	    return ans;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

2. 两层循环统计子数组数量

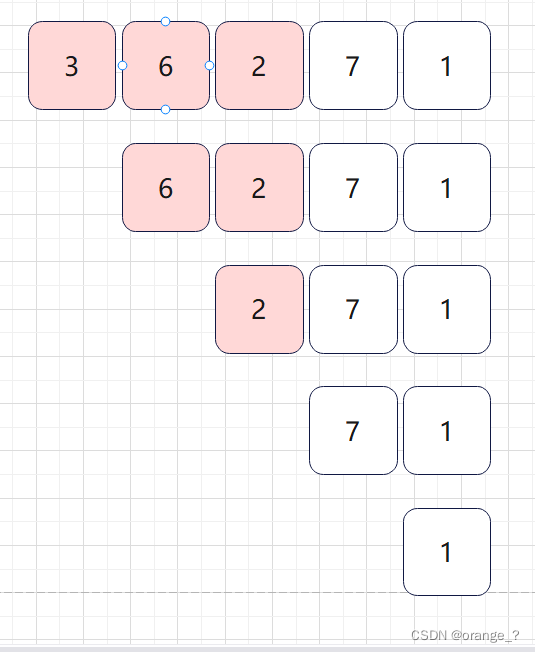
因为三层循环是有重复的计算，然而这些重复的计算又是没必要的，所有可以优化成两层的循环。下图是代码遍历的过程，粉红色是符合最小公倍数的子数组。统计详细：

第一行 [3] [3,6] [3,6,2]
第二行 [6] [6, 2]
第三行 [2]
1
2
3

class Solution{
	private int gcd(int a, int b){
		if (b == 0) return a;
		return gcd(b, a % b);
	}
	
	private int lcm(int a, int b) {
		return a * b / gcd(a, b);
	}
	
	public int subarrayLCM(int[] nums, int k) {
        int ans = 0;
        for (int i = 0; i < nums.length; i++) {
            int res = 1;
            for (int j = i; j < nums.length; j++) {
                res = lcm(nums[j], res);
                if (k == res) ans++;
            }
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22