NC5 二叉树根节点到叶子节点的所有路径和

描述
给定一个二叉树的根节点root，该树的节点值都在数字0−9 之间，每一条从根节点到叶子节点的路径都可以用一个数字表示。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点，不能从子节点到父节点
4.总节点数目为n

例如根节点到叶子节点的一条路径是1→2→3,那么这条路径就用123 来代替。
找出根节点到叶子节点的所有路径表示的数字之和
例如：

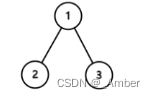
这颗二叉树一共有两条路径，
根节点到叶子节点的路径 1→2 用数字12 代替
根节点到叶子节点的路径 1→3 用数字13 代替
所以答案为12+13=25

数据范围：节点数 0≤n≤100，保证结果在32位整型范围内
要求：空间复杂度 O(n)，时间复杂度 O(n^2)
进阶：空间复杂度 O(n)，时间复杂度 O(n)

示例1
输入：{1,2,3}
返回值：25

示例2
输入：{1,0}
返回值：10

示例3
输入：{1,2,0,3,4}
返回值：257
1
2
3
4
5
6
7
8
9
10
11

牛客网

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 * }
 */

public class Solution {
    /**
     * 
     * @param root TreeNode类 
     * @return int整型
     */
    public int sumNumbers (TreeNode root) {
        // write code here
        if(root == null) return 0;
        int sum = dfs(root,path,0);
        return sum;
    }
    int dfs(TreeNode root,int arr){
        if(root == null){return 0;}
        arr = arr*10+root.val;
        if(root.left == null && root.right == null ) return arr;
        else return dfs(root.left,arr)+dfs(root.right,arr);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

同样的方法，保存的是所有到叶节点的路径，继而求出总sum。

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 * }
 */

public class Solution {
    /**
     * 
     * @param root TreeNode类 
     * @return int整型
     */
    public int sumNumbers (TreeNode root) {
        // write code here
        ArrayList<ArrayList<Integer>> path = new ArrayList<>();
        if(root == null) return 0;
        ArrayList<Integer> arr = new ArrayList<>();
        dfs(root,path,arr);
        int sum = 0;
        for(int i = 0 ;i<path.size();i++){
            arr = path.get(i);
            int val = 0;
            for(int j = 0 ;j<arr.size();j++){
                val  = val*10 + arr.get(j);
            }
            sum += val;
        }
        return sum;
    }
    void dfs(TreeNode root,ArrayList<ArrayList<Integer>> path ,ArrayList<Integer> arr){
        if(root == null){return;}
        arr.add(root.val);
        if(root.left == null && root.right==null) path.add(new ArrayList<>(arr));
        dfs(root.left,path,arr);
        dfs(root.right,path,arr);
        arr.remove(arr.size()-1);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

栈：