wy的leetcode刷题记录_Day41

wy的leetcode刷题记录_Day41

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉

791. 自定义字符串排序

今天的每日一题是：791. 自定义字符串排序

题目介绍

给定两个字符串 order 和 s 。order 的所有单词都是 唯一 的，并且以前按照一些自定义的顺序排序。

对 s 的字符进行置换，使其与排序的 order 相匹配。更具体地说，如果在 order 中的字符 x 出现字符 y 之前，那么在排列后的字符串中， x 也应该出现在 y 之前。

返回 满足这个性质的 s 的任意排列 。

示例 1:
输入: order = “cba”, s = “abcd”
输出: “cbad”
解释: “a”、“b”、“c”是按顺序出现的，所以“a”、“b”、“c”的顺序应该是“c”、“b”、“a”。因为“d”不是按顺序出现的，所以它可以在返回的字符串中的任何位置。“dcba”、“cdba”、“cbda”也是有效的输出。

示例 2:
输入: order = “cbafg”, s = “abcd”
输出: “cbad”

思路

方法一：自定义分数排序：使用一个数组来记录order中字符出现的顺序的分数，未出现的是0。然后根据这个分数实现排序。（关于自定义实现排序请自己查看官方sort解释）
方法二：计数排序：由于题目未要求返回所有的排序顺序，我们可以随意返回一个。我们将出现在order中的字符按顺序放在字符串前半部分，剩下的放在字符串的后半部分。

代码

class Solution {
public:
    string customSortString(string order, string s) {
        int n=order.size();
        int m=s.size();
        vector<int> val(26);
        for(int i=0;i<n;i++)
        {
            val[order[i]-'a']=i+1;
        }
        
        sort(s.begin(),s.end(),[&](char a,char b){
            return val[a-'a']<val[b-'a'];
        });
        return s;
        
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    string customSortString(string order, string s) {
        int n=order.size();
        int m=s.size();
        vector<int> count(26);
        for(int i=0;i<m;i++)
        {
            count[s[i]-'a']++;
        }
        string ans;
        for(int i=0;i<n;i++)//前半部分有序排列s中出现在order中的字符
        {
            if(count[order[i]-'a']!=0)
                ans+=string(count[order[i]-'a'],order[i]);
             count[order[i]-'a']=0;
        }

        for(int i=0;i<26;i++)//把剩下未出现在order中的s中的字符直接累加在后面
        {
            if(count[i]!=0)
                ans+=string(count[i],i+'a');
             count[i]=0;
        }
        return ans;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

收获

简单的模拟题，还是要读清题意，最后实现自己的思路。

110. 平衡二叉树

110. 平衡二叉树

题目介绍

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

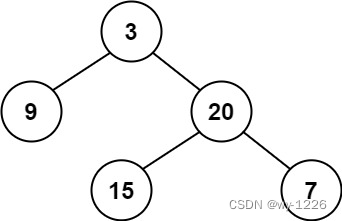
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

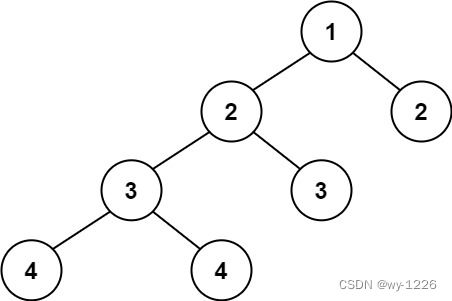
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

思路

根据平衡二叉树的定义可以知道，平衡二叉树的每个节点的左子树和右子树的高度不能相差1，于是我采用dfs中后序的方法从底层向上扩展，如果不满足的话返回-1，否则返回当前子树的高度，作为上面一个节点的左（右）子树进行比较。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        return dfs(root)!=-1;
    }
    int dfs(TreeNode* node) {
        if (node == NULL) {
            return 0;
        }
        int leftDepth = dfs(node->left);
        if (leftDepth == -1) return -1;
        int rightDepth = dfs(node->right);
        if (rightDepth == -1) return -1;
        return abs(leftDepth - rightDepth) > 1 ? -1 : 1 + max(leftDepth, rightDepth);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

收获

收获了平衡二叉树的基本原理，以及如何验证。（废话，没什么收获就是掌握了AVL的一些知识）