2022年ccpc威海站

这一套题将会是我本学期刷的最后一套题，明天就要打icpc西安站了，打完就滚去准备六级和期末考试了，希望自己明天的比赛能够顺利！

A. Dunai

题目链接：Problem - A - Codeforces

 样例输入：

11
skiter Nine 33 Saksa Sneyking
Yatoro TORONTOTOKYO Collapse Mira Miposhka
ana Topson Ceb JerAx N0tail
ana Topson Ceb JerAx N0tail
MATUMBAMAN Miracle MinDContRoL GH KuroKy
shadow bLink Faithbian iceice y
Fear SumaiL UNiVeRsE Aui2000 ppd
Hao Mu xiao8 Banana SanSheng
Loda s4 AdmiralBulldog EGM Akke
Zhou Ferrari430 YYF ChuaN Faith
ArtStyle Dendi XBOCT LighTofHeaveN Puppey
100
Ame 1
NothingToSay 2
Faithbian 3
XinQ 4
y 5
Yuragi 1
bzm 2
ATF 3
Taiga 4
Misha 5
Yatoro 1
TORONTOTOKYO 2
Collapse 3
Mira 4
Miposhka 5
K1 1
ChrisLuck 2
Wisper 3
Gojira 4
Stinger 5
Monet 1
Ori 2
Xxs 3
BoBoKa 4
SiameseC 5
Pakazs 1
DarkMago 2
Sacred 3
Matthew 4
Pandaboo 5
JaCkky 1
Yopaj 2
Fbz 3
TIMS 4
skem 5
Timado 1
Bryle 2
SabeRLight 3
MoonMeander 4
DuBu 5
skiter 1
Nine 2
33 3
Saksa 4
Sneyking 5
dyrachyo 1
BOOM 2
Ace 3
tOfu 4
Seleri 5
Arteezy 1
Abed 2
Nightfall 3
Cr1t 4
Fly 5
Raven 1
Armel 2
Jabz 3
DJ 4
Jaunuel 5
YawaR 1
Quinn 2
LESLAO 3
MSS 4
Fata 5
Lumiere 1
4nalog 2
Vitaly 3
Thiolicor 4
Gardick 5
Pure 1
Stormstormer 2
Tobi 3
Kataomi 4
Fishman 5
Daxak 1
Larl 2
Noticed 3
RodjER 4
SoNNeikO 5
Ghost 1
Somnus 2
Chalice 3
kaka 4
xNova 5
23savage 1
Mikoto 2
kpii 3
Q 4
Hyde 5
Crystallis 1
Nisha 2
Resolut1on 3
Zayac 4
Puppey 5
MATUMBAMAN 1
miCKe 2
zai 3
Boxi 4
iNSaNiA 5

样例输出：

14

题意：一开始给定一个n，代表有n组冠军队伍，每组队伍有5个人，每个人都有一个具体的位置(1~5),接下来输出我们要组队的名单，人数为m，接下来输出m个人，每个人包含名字和位置，我们要对他们进行组队，组队的条件就是每队中至少要有一个人获得过冠军，而且位于1~5的人各有一个，问我们最多能够组成几队。

分析：我们直接统计一下待组队名单中的冠军人数，然后记录一下每个位置的人数，最后这六个值取一个最小值即可，因为冠军的位置可以随意进行调整，我们一开始不考虑每队中都要有冠军这个条件，尽可能按照位置进行组队，然后我们尽可能把冠军分散至不同的队伍中即可。需要注意的是冠军队伍中的人并不是都位于代组队的名单中。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
int main()
{
	int n;
	cin>>n;
	map<string,int>mp;
	for(int i=1;i<=n;i++)
	for(int j=1;j<=5;j++)
	{
		string s;
		cin>>s;
		mp[s]=1;
	}
	int m;
	cin>>m;
	int cnt[10]={0};
	int count=0;
	for(int i=1;i<=m;i++)
	{
		string s;
		int p;
		cin>>s>>p;
		if(mp[s]) count++;
		cnt[p]++;
	}
	int ans=count;
	for(int i=1;i<=5;i++)
		ans=min(ans,cnt[i]);
	printf("%d",ans);
	return 0;
}

C. Grass

题目链接：https://codeforces.com/gym/104023/problem/C

样例输入： 

3
5
0 0
1 1
1 -1
-1 1
-1 -1
3
1 1
4 5
1 4
5
1 0
2 0
3 0
4 0
5 0

样例输出：

YES
0 0
1 1
1 -1
-1 1
-1 -1
NO
NO

题意：给定n个点，找到一个拐点，然后再选择其余的四个点，使得从拐点到其余四个点的连边均没有交点。输出拐点及四个点，如果不存在则直接输出NO。

分析：这个比较简单，我们直接判断一下是否n个点均共线即可知道是否存在这样的点。我们直接对给定的n个点进行遍历，从中找出5个不共线的点，然后暴力枚举符合题意的拐点即可。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e5+10;
long long x[N],y[N];
long long gcd(long long a,long long b)
{
	if(!a) return b;
	return gcd(b%a,a);
}
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n;
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			scanf("%lld%lld",&x[i],&y[i]);
		vector<int>ans;//存储满足题意的5个点坐标
		ans.push_back(1);ans.push_back(2);
		long long dx=x[2]-x[1],dy=y[2]-y[1];
		long long d=gcd(abs(dx),abs(dy));
		dx/=d;dy/=d;
		for(int i=3;i<=n;i++)
		{
			long long Dx=x[i]-x[1],Dy=y[i]-y[1];
			long long D=gcd(abs(Dx),abs(Dy));
			Dx/=D;Dy/=D;
			if(Dx==dx&&Dy==dy)
			{
				if(ans.size()<4) ans.push_back(i);
				continue;//同向共线
			}
			if(Dx==-dx&&Dy==-dy) 
			{
				if(ans.size()<4) ans.push_back(i);
				continue;//反向共线
			}
			for(int j=i;j<=n&&ans.size()<5;j++)
				ans.push_back(j);
			break;
		}
		if(ans.size()<5) puts("NO");
		else
		{
			puts("YES");
			for(int i=0;i<5;i++)//枚举第i个点作为拐点 
			{
				bool flag=true;
				map<pair<long long,long long>,int>mp;
				for(int j=0;j<5;j++)
				{
					if(j==i) continue;
					long long Dx=x[ans[i]]-x[ans[j]],Dy=y[ans[i]]-y[ans[j]];
					long long D=gcd(abs(Dx),abs(Dy));
					Dx/=D;Dy/=D;
					if(mp[{Dx,Dy}])
					{
						flag=false;
						break;
					}
					mp[{Dx,Dy}]=1;
				}
				if(flag)
				{
					printf("%lld %lld\n",x[ans[i]],y[ans[i]]);
					for(int j=0;j<5;j++)
					{
						if(j==i) continue;
						printf("%lld %lld\n",x[ans[j]],y[ans[j]]);
					}
					break;
				}
			}
		}
	}
	return 0;
}

E. Python Will be Faster than C++

题目链接：Problem - E - Codeforces

 样例1输入：

10 1
11 45 14 19 19 8 10 13 10 8

样例1输出：

Python 3.14 will be faster than C++

样例2输入：

10 1
2 2 2 2 2 2 2 2 2 2

样例2输出：

Python will never be faster than C++

题意：给定n个数a1~an，再给定一个k，从第n+1个数开始有a[n+1]=max(2a[n]-a[n-1],0),问最少的m满足am

分析：我们可以发现之后的点全部在n-1个点和第n个点形成的一条直线上，那么由于第n-1个点和第n个点都是大于k的，如果这条直线斜率不是负值，那么就不可能存在这样的m，否则我们直接按照斜率每次变化暴力求解即可。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e7+10;
int a[N];
int main()
{
	int n,k;
	cin>>n>>k;
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	if(a[n]>=a[n-1]) puts("Python will never be faster than C++");
	else
	{
		int kk=a[n]-a[n-1];
		for(int i=n+1;i;i++)
		{
			a[i]=a[i-1]+kk;
			if(a[i]<k)
			{
				printf("Python 3.%d will be faster than C++\n",i);
				break;
			}
		}
	}
	return 0;
}

G. Grade 2

题目链接：Problem - G - Codeforces

样例输入： 

15 2
1 4
11 4514

样例输出：

2
2252

题意：给定一个x和一个n，n代表询问次数，每次询问给定一个区间[l,r],需要给出下列表达式的值

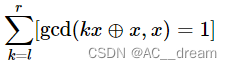
 分析：一开始看到询问的范围是1e12，那么就猜测是有循环节的，通过打表发现gcd(kx^x,x)循环节长度为第一个大于等于x的2的幂次，那么我们直接暴力求解循环节即可，然后利用循环节进行简化计算。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e7+10;
long long sum[N];
long long circle=1;
long long gcd(long long a,long long b)
{
	if(!a) return b;
	return gcd(b%a,a);
}
long long cal(long long r)
{
	return sum[circle]*(r/circle)+sum[r%circle];
}
int main()
{
	long long x,n;
	cin>>x>>n;
	while(circle<x) circle<<=1;
	for(int i=1;i<=circle;i++)
		sum[i]=sum[i-1]+(gcd((x*i)^x,x)==1);
	while(n--)
	{
		long long l,r;
		scanf("%lld%lld",&l,&r);
		printf("%lld\n",cal(r)-cal(l-1));
	}
	return 0;
}

J. Eat, Sleep, Repeat

题目链接：Problem - J - Codeforces

样例输入： 

5
2 0
1 2
2 1
1 2
0 1
3 2
3 3 4
0 2
1 1
3 2
2 3 3
1 2
0 1
5 4
6 7 8 12 17
1 1
2 1
9 0
10 1

样例输出：

Pico
FuuFuu
Pico
FuuFuu
Pico

题意：一开始给定n个数和m个限制，Pico和FuuFuu轮流对这n个数进行操作，每次操作都是选择n个数中的一个进行减1操作，每个限制给定一个x和y，代表操作过程中x的出现次数不能大于y，谁最后不能操作了谁就输掉了游戏，问谁最后会获胜。

分析：通过分析一些样例不难发现，如果某个限制是x的出现次数不能超过0，那么一开始给定的数中大于x的数都不可能减小至x，而且这个时候如果对于数x+1的出现次数没有限制的话那么就可以把所有大于x的数降低至x+1（必须保证比x大的第一个限制为0的数是大于当前数的），如果x+1的出现次数是cnt的话，那么我们的最终结果应该是使得x+1的出现次数小于等于cnt，因为死局是当且仅当所有数都无法再进行操作，所以当且仅当所有数都到下限了才会进入死局。按照这个策略我们可以先按照限制次数为0的数进行分类，然后对于每个区间内的数都按照这个策略尽可能地使其值达到下限，最后计算一下操作次数，那么看一下总的操作次数是奇数还是偶数就可以知道是谁获胜了。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e5+10;
int a[N];
struct node{
	int h,cnt;
}p[N];
bool cmp(node a,node b)
{
	return a.h<b.h;
}
int st[N];
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n,m;
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++)
			scanf("%d",&a[i]);
		sort(a+1,a+n+1);
		map<int,int>mp;//mp[i]记录i的最大限制次数
		for(int i=1;i<=m;i++)
		{
			scanf("%d%d",&p[i].h,&p[i].cnt);
			mp[p[i].h]=p[i].cnt;
		}
		sort(p+1,p+m+1,cmp);
		int tt=0;
		st[++tt]=-1;
		for(int i=1;i<=m;i++)
			if(p[i].cnt==0) st[++tt]=p[i].h;
		st[++tt]=1e9+1;
		long long ans=0;
		for(int i=2;i<=tt;i++)
		{
			int l=lower_bound(a+1,a+n+1,st[i-1]+1)-a;
			int r=lower_bound(a+1,a+n+1,st[i])-a-1;
			int len=r-l+1;
			for(int i=l;i<=r;i++)
				ans+=a[i];
			for(int h=st[i-1]+1;len&&h<st[i];h++)
			{
				if(mp.count(h))
				{
					long long t=min(mp[h],len);
					len-=t;
					ans-=t*h;
				}
				else
				{
					ans-=len*h;
					len=0;
				}
			}
		}
		if(ans&1) puts("Pico");
		else puts("FuuFuu");
	}
	return 0;
}