蓝桥杯2022年第十三届决赛真题-修路

题目描述

这天，小明在修路。

他需要修理两条平行的道路 A, B，两条路上面分别有 n 个和 m 个点需要维修，它们相对于道路起点的距离分别为 a1, a2, . . . , an 和 b1, b2, b, …, bm。如图，两条路之间的距离为 d 且它们起点 (最左端) 的连线和两条路都垂直。小明的起点为道路 A 的起点，他需要尽可能快地遍历这些需要维修的 n + m 个点，他既可以沿着道路 向右 行走，也可以在两条道路之间的空地上 随意 行走。

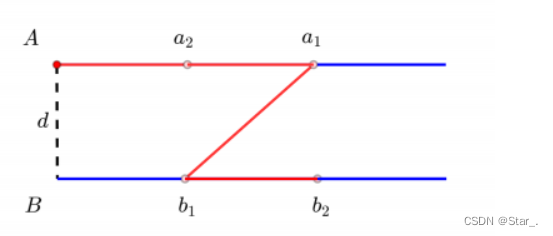
小明想知道遍历这些点的最短路程是多少。

输入格式

输入共三行，第一行为三个正整数 n, m, d。
第二行为 n 个由空格隔开的正整数 a1, a2, …, an。
第三行为 m 个由空格隔开的正整数 b1, b2, …, bm。

输出格式

一行，一个浮点数，表示答案，保留两位小数。

样例输入

2 2 2
2 1
1 2

样例输出

5.24

思路：(被一个函数恶心到了)，求最短路径，因为某个点它会从A路的前一个点或者B路的某个点走过来，所以判断是dp题。然后我就开始想先初始化状态，一开始设置的二维数组，表示已走过A路前i个点和B路的前j个点。然后再思考状态转移方程的时候发现不能确定我最后是在A路还是B路，所以我就再加了一维表示我现在在A路还是B路。
首先，我们先考虑

初始化

先把a,b这两数组按升序排下序，这题真的太老六了，我也是在运行样例的时候发现的。
如果我们一直没修B,一直修A,那么在A路上
dp[i][0][0] = a[i];
在B路上，Double.POSITIVE_INFINITY表示正无穷（学到了）
dp[i][0][1] = Double.POSITIVE_INFINITY;

如果一直修B,没修A,
在A路上，
dp[0][i][0] = Double.POSITIVE_INFINITY;
在B路上，
注意了，小明一开始在A路的起点，如果要先修B,必须先走到B才行

dp[0][0][1] = d;//一开始先走到B

dp[0][1][0] = Double.POSITIVE_INFINITY;//无法在最后停在A路的情况下，A路一个不走然后走一个B
dp[0][1][1] = hypot(d, b[1]);//从A的起点先走B的第一个点。

dp[0][i][1] = b[i] - b[i - 1] + dp[0][i - 1][1];//一直走B

状态转移方程

这个就容易多了
当前若是要求dp[i][j]
某个点若最后停在了A路，那么他可以由A路前边那个点(i-1)走过来，或者有B路的j点走过来
dp[i][j][0] = Math.min(dp[i - 1][j][0] + a[i] - a[i - 1], dp[i - 1][j][1] + hypot(d, a[i] - b[j]));
某个点若最后停在了B路，那么他可以由B路前边那个点(i-1)走过来，或者有A路的j点走过来
dp[i][j][1] = Math.min(dp[i][j - 1][1] + b[j] - b[j - 1], dp[i][j - 1][0]+ hypot(d, a[i] - b[j]));

hypot函数欧几里得范数，而不会出现中间上溢或下溢（直接用Math.sqrt()老是数组越界，很烦）

import java.util.*;
import static java.lang.Math.hypot;
public class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n=sc.nextInt();
		int m=sc.nextInt();
		int d=sc.nextInt();
		int[] a = new int[n + 1];
		int []b = new int[m + 1];
		double[][][] dp = new double[n + 1][m + 1][2];
		for (int i = 1; i <= n; i++) a[i] = sc.nextInt();
		for (int i = 1; i <= m; i++) b[i] = sc.nextInt();
		Arrays.sort(a, 1, n + 1);
		Arrays.sort(b, 1, m + 1);
		for (int i = 1; i <= n; ++i) {
			dp[i][0][1] = Double.POSITIVE_INFINITY;
			dp[i][0][0] = a[i];
		}
		if (m > 0) {
			dp[0][1][0] = Double.POSITIVE_INFINITY;
			dp[0][1][1] = hypot(d, b[1]);
			dp[0][0][1] = d;
		}
		for (int i = 2; i <= m; ++i) {
			dp[0][i][0] = Double.POSITIVE_INFINITY;
			dp[0][i][1] = b[i] - b[i - 1] + dp[0][i - 1][1];
		}
		for (int i = 1; i <= n; ++i)
			for (int j = 1; j <= m; ++j) {
				dp[i][j][0] = Math.min(dp[i - 1][j][0] + a[i] - a[i - 1], dp[i - 1][j][1] + hypot(d, a[i] - b[j]));
				dp[i][j][1] = Math.min(dp[i][j - 1][1] + b[j] - b[j - 1], dp[i][j - 1][0]+ hypot(d, a[i] - b[j]));
			}
		System.out.println(String.format("%.2f", Math.min(dp[n][m][0],dp[n][m][1])));
		sc.close();
	}
	
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39