希尔排序详解

目录

希尔排序的别名

希尔排序的思想

现实举例

数据举例

第一轮：

第二轮：

第三轮：

希尔排序和插入排序的比较

拿以上述例子举例：

算法实现：

---

希尔排序的别名

希尔排序是插入排序的一种又称缩小增量排序

是直接插入排序算法的一种更高效的改进版本

希尔排序是非稳定排序算法。该方法因D,L,Shell于1959年提出而得名

希尔排序的思想

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序，随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止

现实举例

可以用打擂台的方式来进行理解，最终比赛结果的排行榜就就可以看做是一个排序的降序

擂台规则：

                     第一轮：  假设一共有8个人，那么就设置增量为4个，对这8个人依次给予号码牌，分别为12341234，号码牌相同的进行格斗，分出名次

                        第二轮：设置增量为2，根据第一轮比赛结果，再依次给予号码牌，分别为12121212，号码牌相同的进行格斗，分出名次

                        第三轮：设置增量为1，根据第二轮比赛结果，在依次给予号码牌，分别为11111111，号码牌相同的进行格斗，分出名次，这就是最后的比赛结果。

数据举例

再以数字序列举例：

                                85761324

第一轮：

                一共有8个元素，增量设置为4，元素依次为1234，1234，相同的号码进行插入排序

第二轮：

                第一轮的排序后的结果，增量设置为2，元素依次为12,12,12,12，相同的号码进行插入排序

第三轮：

                第二轮的排序结果，增量设置为1，元素依次为1，1,1,1,1,1,1,1， 相同的号码进行插入排序，结果为最终的排序结果

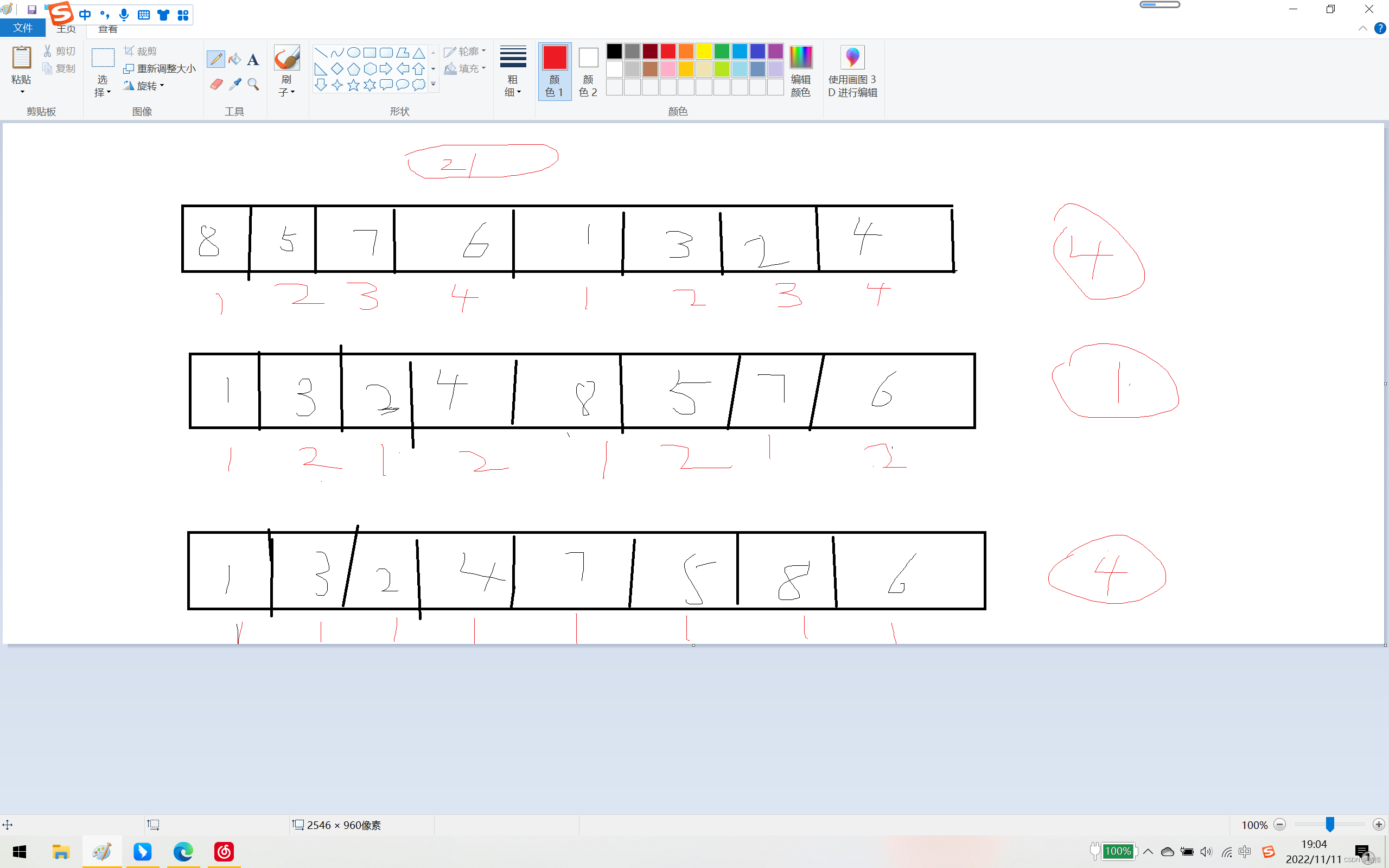
希尔排序和插入排序的比较

希尔排序是插入排序的一种，其内核其实还是插入排序

希尔排序是插入排序的优化算法，

拿以上述例子举例：

                                        如果要使用希尔排序的话一共要进行9次，如果要使用插入排序的话一共需要21次，显而易见：希尔排序要比插入排序高效很多

算法实现：

根据例子的排序过程可写成以下的算法

#include
#include
using spacename std;
void shell_sort(int arr[], int size)
{
	if (size <= 1)
	{
		return;
		int temp, j;
		int jump = size >> 1;//jump是增量
		while (jump != 0)
		{
			for (int i = jump; i
			{
				temp = arr[i];
				j = i - jump;
				while (j>-jump&&temp < arr[j])
				{
					arr[j + jump] = arr[j];
					j -= jump;
				}
				arr[j + jump] = temp;
			}
		}
	}