wy的leetcode刷题记录_Day40

wy的leetcode刷题记录_Day40

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉

790. 多米诺和托米诺平铺

今天的每日一题是：790. 多米诺和托米诺平铺

题目介绍

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 “L” 的托米诺形。两种形状都可以旋转。

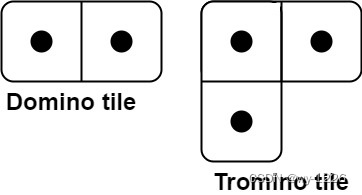
给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

示例 1:

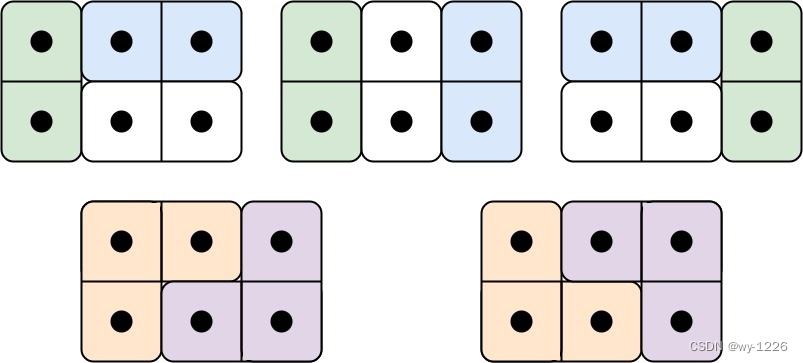
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。

示例 2:
输入: n = 1
输出: 1

思路

动态规划:

1. 确定dp数组的含义：dp[i]表示平铺到第i列时各个状态对应的平铺方法数量，其中有四种不同的状态：

• 一个正方形都没有被覆盖，记为状态 0；
• 只有上方的正方形被覆盖，记为状态 1；
• 只有下方的正方形被覆盖，记为状态 1；
• 上下两个正方形都被覆盖，记为状态 3。

2. 确定dp数组的递推公式：
   由dp数组对应的含义可以知道：状态0，一个都没有覆盖其实就等于上列中的俩个正方形都被覆盖的情况；状态1：可以由上一个状态0+一个L型铺成或者上一列状态2+一个多米诺型；状态2：上一列状态0+L或者上一列状态1+一个多米诺型；状态3：上一列状态0+俩个多米诺型或者上一列状态1+一个L 型或者上一列状态2+一个L型或者上一列状态3+一个多米诺型；

dp[i][0]=dp[i−1][3]
dp[i][1]=dp[i−1][0]+dp[i−1][2]
dp[i][2]=dp[i−1][0]+dp[i−1][1]
dp[i][3]=dp[i−1][0]+dp[i−1][1]+dp[i−1][2]+dp[i−1][3]

​

3. 初始化
   根据题意可推出下列初始化dp数组公式：

dp[0][0] = 0;
dp[0][1] = 0;
dp[0][2] = 0;
dp[0][3] = 1;
1
2
3
4

代码

const long long mod = 1e9 + 7;
class Solution {
public:
    int numTilings(int n) {
        vector<vector<long long>> dp(n + 1, vector<long long>(4));
        dp[0][3] = 1;
        for (int i = 1; i <= n; i++) {
            dp[i][0] = dp[i - 1][3] % mod;
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % mod;
            dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
            dp[i][3] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][3]) % mod;
        }
        return dp[n][3];
    }
};


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

收获

巩固了动态规划的知识。

222. 完全二叉树的节点个数

222. 完全二叉树的节点个数

题目介绍

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

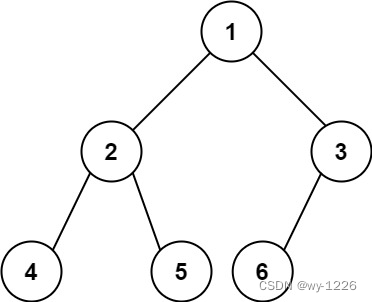
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：
输入：root = []
输出：0

思路

首先计算左右子树的深度，如果左子树深度等于右子树深度说明左子树是完全二叉树，完全二叉树的节点个数可以通过深度直接求出来（位运算更快），如果左子树深度大于右子树深度的话说明右子树是完全二叉树，同理…

代码

class Solution {
public:
    // 统计树的深度
    int countLevels(TreeNode* root) {
        int levels = 0;
        while (root) {
            root = root->left; levels += 1;
        }
        return levels;
    }
    int countNodes(TreeNode* root){
        // 2. 利用完全二叉树性质简化遍历次数
        if(root == nullptr) return 0;
        int left_levels = countLevels(root->left);
        int right_levels = countLevels(root->right);
        // 左子树深度等于右子树深度, 则左子树是满二叉树
        if(left_levels == right_levels){
            return countNodes(root->right) + (1<<left_levels);
        }else{
            return countNodes(root->left) + (1<<right_levels);
        }
    }
};


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

收获

掌握了完全二叉树的相关知识。