密码学 | 期末考前小记

密码学 | 期末考前小记

————

密码学课程要考试了，又是最后两天赶紧学一点。根据密码学的几个重点密码算法，我主要看b站的视频理解算法的过程，然后做了以下笔记加强。不先看视频理解下面的可能也不太好食用。

————

rc4 加密算法

1 , 通过密钥调度算法KSA初始化状态矢量S（S就是一个随机数发生器，称为S-box）
s盒256个值，key 也 mod 出256个值
j=j+s[i]+k[i]
s盒i,j交换

2 , 再通过伪随机数生成算法PRGA得到密钥流keystream
3 , 密钥流keystream 与明文进行xor运算得到密文，解密用 密钥流与密文xor
j=j+s[i]
s盒i，j交换
生成伪随机数：
t=s[i]+s[j]
异或得到密钥
d[k]^=s[t]

————

A5-1序列密码

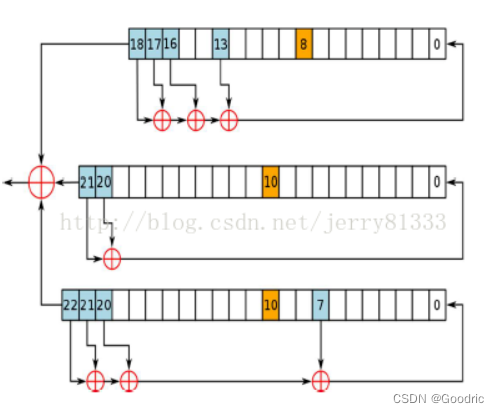
A5/1算法使用了三个LFSR （线性反馈移位寄存器，LFSR）

X: 19 bits (x18,x17,x16, …,x0)
Y: 22 bits (y21,y20,y19, …,y0)
Z: 23 bits (z22,z21,z20, …,z0)
1
2
3

19+22+23 = 64 共 64 bit
要用到的密钥也是 64 bit 的。

三个 LFSR 的反馈函数为：
fx = x19⊕x18⊕x17⊕x14⊕1
fy = y22⊕y21⊕1
fz = z23⊕z22⊕z19⊕z18⊕1

密钥 k = k64k63…k1

一、三个 LFSR 的初始化填充

1、64个位置都填充为0
2、每个 LFSR 都要左移运动64次
比如第一次规则运动 x0 的位置的内容为 反馈函数的结果和 k1 异或得到的的结果
即 x0 的内容变为 x19⊕x18⊕x17⊕x14⊕1 ⊕ k1
3 个 LFSR 都这样移动 64 次

3、每个 LFSR 再规则运动 22 次
和前面一步不同的是
比如第一次规则运动 x0 的位置的内容为 反馈函数的结果和 帧序号 异或得到的的结果
即 x0 的内容变为 x19⊕x18⊕x17⊕x14⊕1 ⊕ 帧序号
（这个帧序号不知道是啥，可能会给出吧）

二、加密

根据钟控信号左移
钟控信号规定了来自3个 LFSR 的位置：x8y10z10 ，即 LFSR-x 的第9级，LFSR-y 的第11级，LFSR-z 的第 11级
比如 x8y10z10 = 001 ，以则多原则，001中 0 数量更多 ，这里就是 x ，y 左移一位
比如 x8y10z10 = 111 ，就是 x,y，z 都左移一位

连续取 100 次钟控信号进行移位，
再次取 114 次钟控信号，每次将 3 个 LFSR 最高级的值输出，相互异或得到结果，得到 1bit 乱数 di

总共得到 114 个乱数，mi 为114 位明文
ci = mi ⊕ di

解密
连续取 100 次钟控信号进行移位，
再次取 114 次钟控信号，得到 114 个乱数 di
mi = ci ⊕ di

————

rsa 加密算法

————

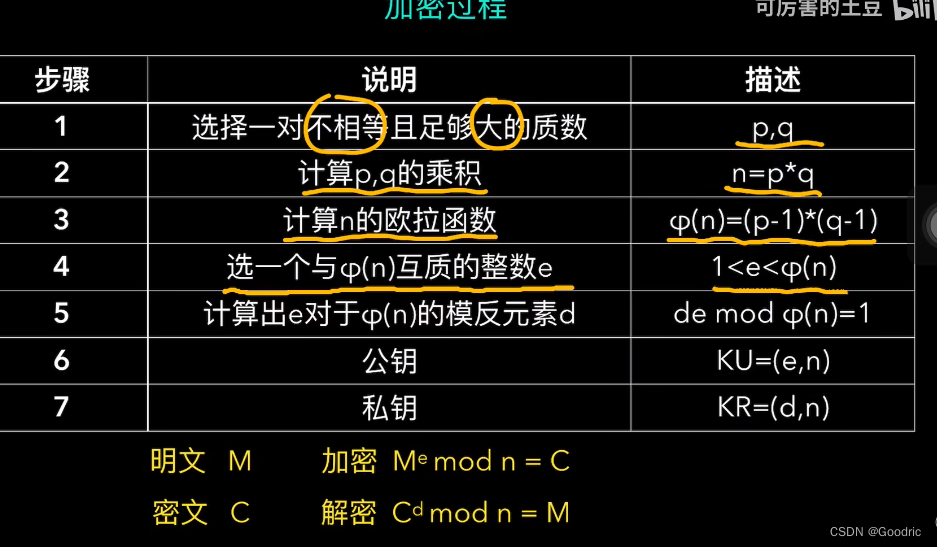
des加密算法

对明文进行操作：

一、IP置换

二、十六轮迭代

64bit 明文分成 R0,L0各 32bit 。
L1 直接得到，L1=R0，下面是R1的求法

1、R0进行 E 扩展：32->48
每四位两边扩展，扩展的位是相邻四位边上那个数，
如 1010 1001 扩展之后为 110101010011

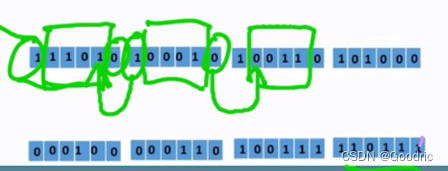
2、异或
E盒扩展后得到 48 bit 和 48 bit 密钥 进行异或。

3、s盒压缩：48->32
48位分为8块，每块6位要压缩为4位
头尾2位为行数，中间4位为列数
得到行列在表里找到值，转为4位二进制，即压缩完成

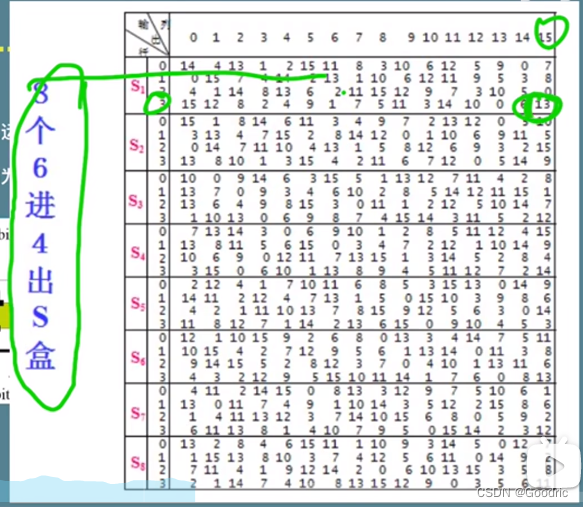
4、P盒置换
s盒压缩后根据p盒置换

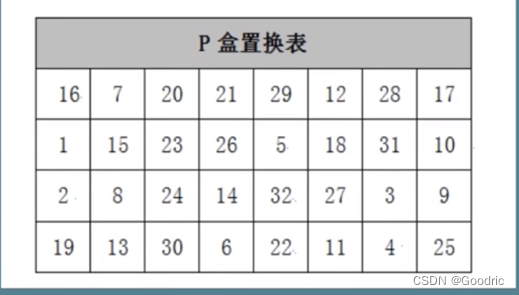
5、得到的 32 位和 L0 异或，得到 R1

这样就结束了一轮迭代，总共进行十六轮
比如下一轮，L2=R1 ，R2根据上面方法求

三、IP-1逆置换

十六轮之后，L16 和 R16 拼接在一起进行逆置换。得到密文。

密钥生成

密钥64位，56位参与运算，其余八位为校验位（8，16，24，32，40，48，56，64）
上面迭代的第二步和48位密钥异或用到了 48 位 密钥。
去掉 8 位校验位，剩 56 bit
分成 C0 , D0 两部分，各 28 bit
C0 , D0 拼接在一起根据表置换，得到 48 bit 的密钥

第一轮迭代要用到 C1 , D1 拼接起来进行置换成 48 bit ，
而 C1，D1是根据 C0 D0 循环左移得到，每次迭代有规定的左移次数
如
C0：1101
D0：1010
循环左移后：
C1：1011
D1：0101

————

Aes加密算法

明文长度固定128位
密钥长度128，192，256

一、初始变换

明文十六字节（128bit）
密钥十六字节（128bit）
都是4×4矩阵，两个矩阵进行异或得到 十六字节 的结果

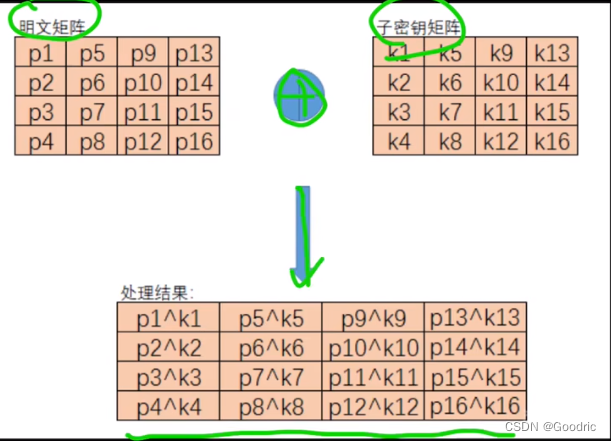
二、九轮循环运算

1、字节代换
根据 S表（s-box）对每个字节进行代换

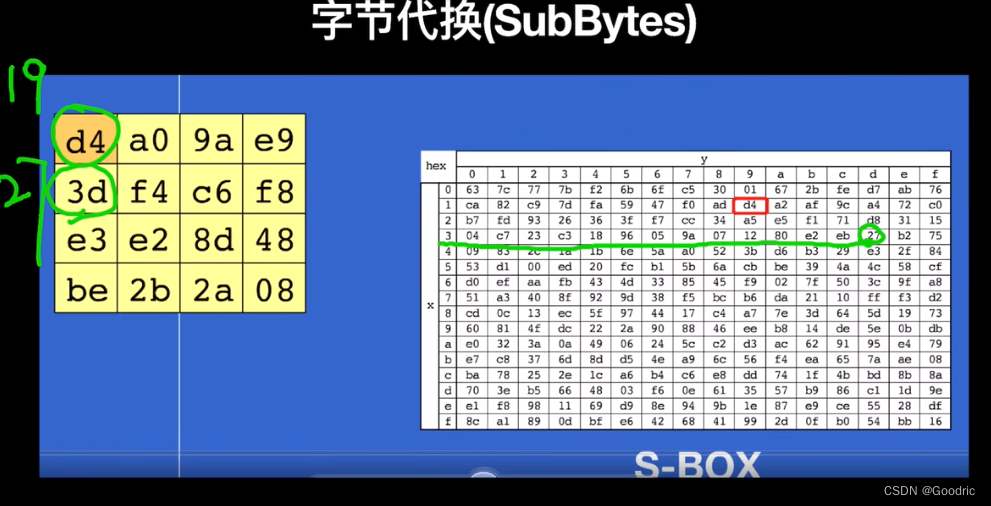
2、行移位
第一行不变
第二行左移1个字节
第三行左移2各字节
第四行左移3各字节

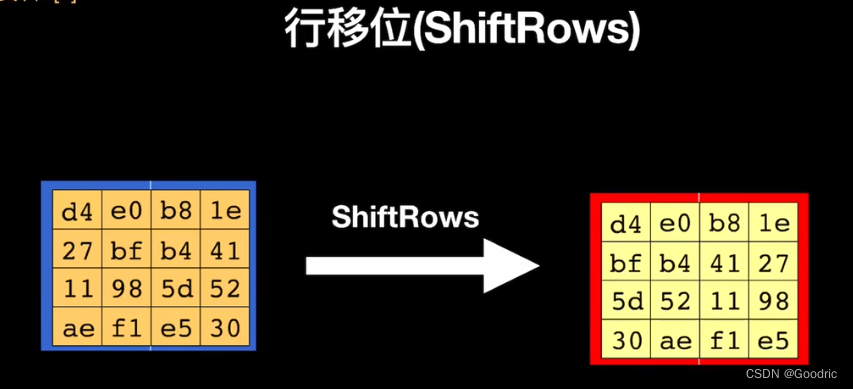
3、列混合
要左乘一个固定的矩阵
但不是普遍意义上的矩阵相乘

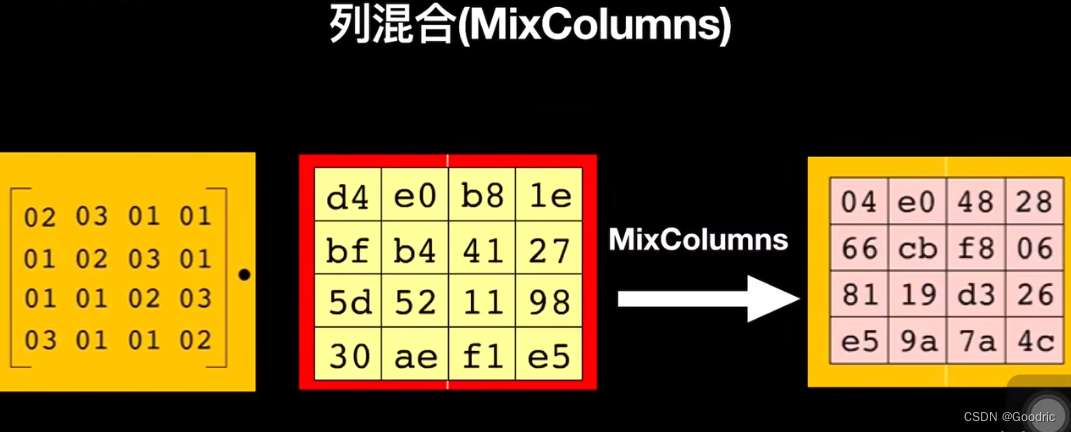
普通定义的相乘比如求第一个数是第一行×第一列为：
02×d4 + 03×bf + 01×5d + 01×30

这里 + 要变成⊕
02×d4 ⊕ 03×bf ⊕ 01×5d ⊕ 01×30

然后乘法通过二进制：

02×d4
=00000010 × 11010100       11010100(a7a6a5a4a3a2a1a0)
=10101000 ⊕ 00011011          (因a7=1，要和 00011011 异或)（10101000(a6a5a4a3a2a1a00)）
=10110011
1
2
3
4

4、轮密钥加
列混合之后的结果和扩展后的第一轮密钥进行异或

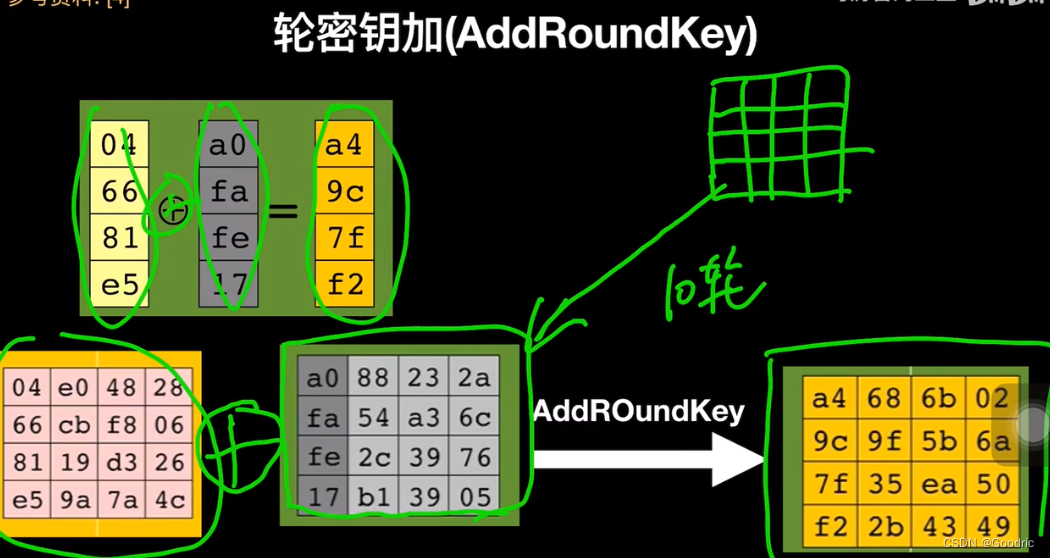
三、1轮最终轮

和前面的轮循环不同在于没有列混合的步骤。
即最终轮步骤为 字节代换—行位移—轮密钥加

十轮密钥扩展

由原4列密钥向右边一列一列进行扩展。

每一轮密钥的4列中，后三列的列数不是4的倍数，扩展规则为：
w[i] = w[i-4] ⊕ w[i-1]
即要求那列由 前一列 和 前第四列 异或得到
如
w[6] = w[2] ⊕ w[5] (列数是从 0 开始向右数)

是 4 的倍数的列数扩展，即所扩展的每轮密钥的第一列的扩展规则：
W[i] = W[i-4] ⊕ T(W[i-1])

T(W[i-1]) 的运算有三步：
1、字循环
将 W[i-1] 左移一位，即 [b0 , b1 , b2 , b3] 变换为 [b1 , b2 , b3 , b0]

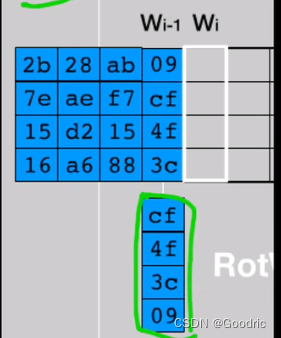
2、字节代换
和前面的轮循环中的字节代换一样，对照 s 表(s-box ) 进行代换

3、轮常量异或
常量是固定的，共十列
将字节代换的结果和对应列数的常量进行异或。（求的是第一轮密钥的第一列就和常量的第一列异或，求的是第二轮密钥的第一列就和常量的第二列异或）
这里就得到 T(W[i-1]) 的结果了。

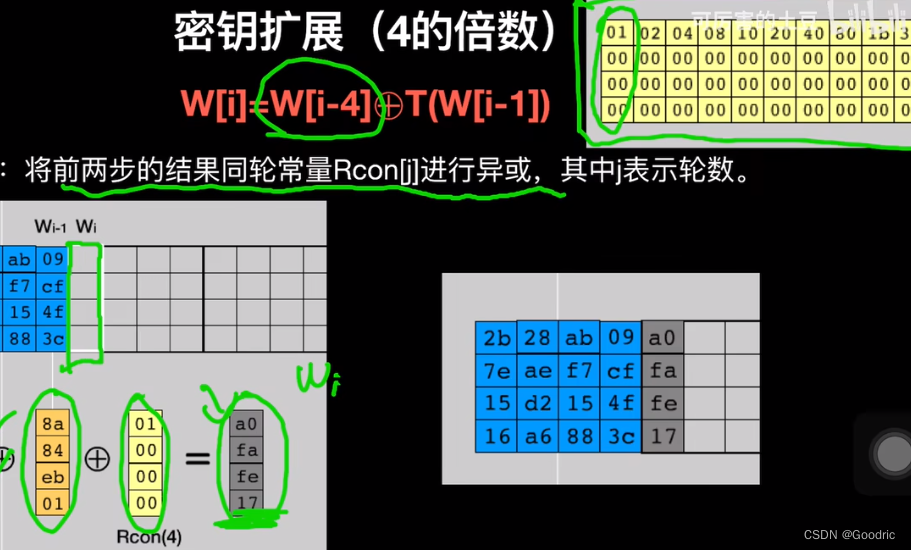
根据公式 W[i] = W[i-4] ⊕ T(W[i-1]) 再和 W[i] 的 前第四列 进行异或即可得到 W[i]
密钥扩展的方法就是这样了。

————

ECC加密算法

mod(23) 指有限域 GF(23)
a,b=1，A(0,1)
求2A
计算：
k=12 1/2mod23 = 12 2n%23=1%23=1, n=12
x3=6
y3=19 -73mod23 = 19 23*4-73=92-73=19

得到 2A(6,19)

————

中国剩余定理

求x例题：

————

背包加密算法

私钥：（2，3，6，13）
m = 50
w = 11

求公钥
私钥[i]*w mod m
得到 公钥为：（22，33，16，43）

加密
明文 10011100
明文根据密钥有多少个则分为多少位一组，这里是四位1组
1001 1100
每组中为 1 的位置对应公钥的位置相加
22+43=65
22+33=55

得到密文： 65，55

求 w^-1 （w逆）w=11 ，求逆运算

w-1=1 mod 50
50 = 11*4 + 6 …… q1 = 4
11 = 6*1+5 …… q2 = 1
6 = 5*1 + 1 到 1 停止 …… q3 = 1

b[-1]=0 b[0]=1
b[i] = -1*b[i-1]*q[i]+b[i-2]
b[1] = -1*1*4+0 = -4
b[2] = -1*(-4)*1+1 = 5
b[3] = -1*5*1 + (-4) = -9

w-1 = -9
w-1 = -9 mod 50 = 41
w逆=41

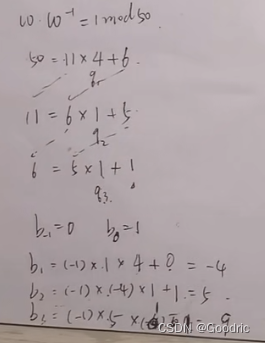
解密：
密文 65，55
65*w-1 mod 50

65*41 mod 50 = 15
55*41 mod 50 = 5

根据私钥（2，3，6，13）
15=2+13
对应密钥中的第 1 ，4 位置，1001
5=2+3
对应密钥中的第 1，2 位置 1100

得到明文 10011100

————

Diffie-Hellman密钥交换算法

已知 a，q
私钥Xa
计算公钥 Ya = a^Xa mod q
得到对方公钥
计算共享密钥
Yb^Xa mod q

————

考完除了上面算法能解决的，这次考试的题目还有没学到的内容~寄！
比如有题目仿射密码，三级移位寄存器的设计