随想录一刷Day52——动态规划

Day52_动态规划

41. 最长递增子序列

300. 最长递增子序列
思路：

1. dp[i]表示以nuims[i]为结尾的子序列的最大长度
2. 递推公式：遍历 $0-i$ 如果前面出现比nums[i]小的数，更新 dp[i] = max(dp[i], dp[j] + 1)
3. 初始化 ：每个数字对应的子序列长度至少为1，其本身
4. 遍历顺序，从前往后

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int nums_size = nums.size();
        if (nums_size == 0) return 0;
        vector<int> dp(nums_size, 1);
        int ans = 1; // 到这里子序列的长度至少是1
        for (int i = 1; i < nums_size; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = max(dp[i], dp[j] + 1);
                    ans = max(dp[i], ans);
                }
            }
        }
        // for (int i = 0; i < nums_size; i++) cout << dp[i] << endl;
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

42. 最长连续递增序列

674. 最长连续递增序列
思路：

记录以当前nums[i]为结尾的最长连续上升子序列的长度，当出现数值减小时，重新计数

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int nums_size = nums.size();
        vector<int> dp(nums_size, 1);
        int ans = 1;
        for (int i = 1; i < nums_size; i++) {
            if (nums[i] <= nums[i - 1]) dp[i] = 1;
            else dp[i] = dp[i - 1] + 1;
            ans = max(ans, dp[i]);
        }
        // for (int i = 0; i < nums_size; i++) cout << dp[i] << endl;
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

43. 最长重复子数组

718. 最长重复子数组
思路：

1. dp[i][j]代表nums1遍历到第i个，nums2遍历到第j个时最长重复子数组的长度
2. 递推公式：当nums1[i] == nums2[j]时，由上一个状态转移过来 dp[i][j] = dp[i-1][j-1]
3. 初始化：初始化dp[i][0]和dp[0][j]均为0，此时没有能匹配上的
4. 遍历顺序，外层nums1后，内层nums2，顺序无关怎样都行

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int nums1_size = nums1.size();
        int nums2_size = nums2.size();
        int result = 0;
        vector<vector<int>> dp(nums1_size + 1, vector<int>(nums2_size + 1, 0));
        for (int i = 1; i <= nums1_size; i++) {
            for (int j = 1; j <= nums2_size; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                result = max(result, dp[i][j]);
            }
        }
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

滚动数组优化，为什么维度是nums2.size()呢，看看下面这张图就明白了（再偷图一张），其实就是和背包类似
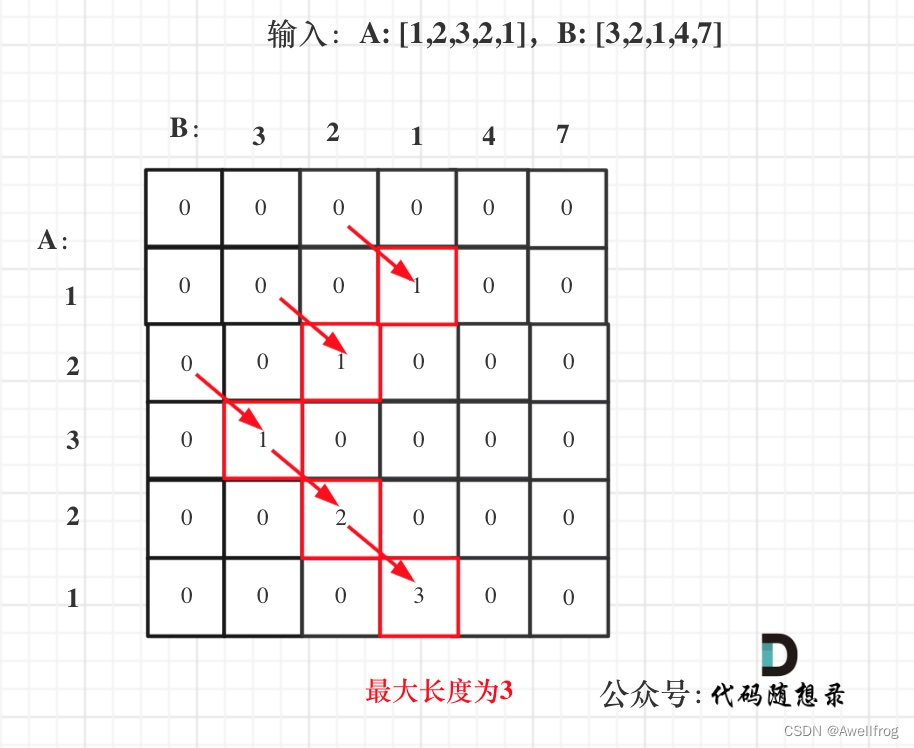
把上一行复制下来，继续使用，为了不覆盖前面的数值，内层循环从后往前

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int nums1_size = nums1.size();
        int nums2_size = nums2.size();
        int result = 0;
        vector<int> dp(nums2_size + 1, 0);
        for (int i = 1; i <= nums1_size; i++) {
            for (int j = nums2_size; j > 0; j--) { // 内层循环从后往前
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[j] = dp[j - 1] + 1;
                } else dp[j] = 0;
                result = max(result, dp[j]);
            }
        }
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18