【力扣题解】石子游戏

🔗 题目链接

题目描述

Alice 和 Bob 用几堆石子在做游戏。一共有偶数堆石子，排成一行；每堆都有 正 整数颗石子，数目为 piles[i] 。

游戏以谁手中的石子最多来决出胜负。石子的 总数 是 奇数 ，所以没有平局。

Alice 和 Bob 轮流进行，Alice 先开始 。每回合，玩家从行的 开始 或 结束 处取走整堆石头。这种情况一直持续到没有更多的石子堆为止，此时手中 石子最多 的玩家 获胜 。

假设 Alice 和 Bob 都发挥出最佳水平，当 Alice 赢得比赛时返回 true ，当 Bob 赢得比赛时返回 false 。

题目分析

我们来假设piles[i] = [1, 5, 7, 4]，我们把 Alice 取到的石子数看为正，Bob 取到的石子数为负。

• Alice 先手，取 1，得到 1 分

  剩下数组为[5, 7, 4]，此时 Bob 作为先手。在剩下的这些中，Bob 最多可以得到 9 分，Alice 可以得到 7 分。最终 Alice 会得到的分数是-2 分。因为 Alice 开始得到了 2 分，所以最终 Alice 会得到的分数是-1 分，Alice 输。

• Alice 先手，取 4，得到 4 分

  剩下为[1, 5, 7]，此时 Bob 作为先手。在剩下的这些中，Bob 可以得到 8 分，Alice 可以得到 5 分，最终 Alice 得了-3 分。因为 Alice 一开始得到了 4 分，所以最终 Alice 得到 1 分，Alice 赢。

通过上面对比，Alice 作为先手，应该先取 4，就会胜利。

这道题，我们会发现，piles数组是不断变化的，而且 Alice 和 Bob 轮流作为先手玩家来取石子，因此此题可以采用动态规划的方法来解决。dp[i][j]表示当数组剩下i~j个元素时，此时先手玩家会得到的分数。动态规划方程如下：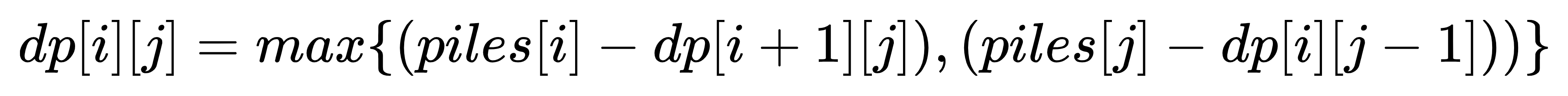

根据动态规划方程，我们可以得到如下的表格。

然后，我们按照 ①~⑥ 的顺序，依次填入值：

①：i=0, j=1，代入公式dp[0][1] = MAX{ (piles[0]-dp[1][1]), (piles[1]-dp[0][0])，piles[0]=1, dp[1][1]=5, piles[1]=5, dp[0][0]=1。所以，dp[0][1]最终结果为4。

②：i=1, j=2，代入公式dp[1][2] = MAX{ (piles[1]-dp[2][2]), (piles[2]-dp[1][1])，piles[1]=5, dp[2][2]=7, piles[2]=7, dp[1][1]=5。所以，dp[1][2]最终结果为2。

③：i=0, j=2，代入公式dp[0][2] = MAX{ (piles[0]-dp[1][2]), (piles[2]-dp[0][1])，piles[0]=1, dp[1][2]=2, piles[2]=7, dp[0][1]=4。所以，dp[0][2]最终结果为3。

④：i=2, j=3，代入公式dp[2][3] = MAX{ (piles[2]-dp[3][3]), (piles[3]-dp[2][2])，piles[2]=7, dp[3][3]=4, piles[3]=4, dp[2][2]=7。所以，dp[2][3]最终结果为3。

⑤：i=1, j=3，代入公式dp[1][3] = MAX{ (piles[1]-dp[2][3]), (piles[3]-dp[1][2])，piles[1]=5, dp[2][3]=3, piles[3]=4, dp[1][2]=2。所以，dp[1][3]最终结果为2。

⑥：i=0, j=3，代入公式dp[0][3] = MAX{ (piles[0]-dp[1][3]), (piles[3]-dp[0][2])，piles[0]=1, dp[1][3]=2, piles[3]=4, dp[0][2]=3。所以，dp[0][3]最终结果为1。

同样的方法，我们可以依次把剩下的表格内容填充完成。

最终，我们发现dp[0][3]的值是1，所以Alice赢。

题解代码

/**
 * @param {number[]} piles
 * @return {boolean}
 */
var stoneGame = function (piles) {
  const len = piles.length;
  // 构造二维数组表格
  const dp = new Array(len);
  for (let i = 0; i < len; i++) {
    dp[i] = new Array(len);
    dp[i][i] = piles[i];
  }
  // 填充表格
  for (let j = 1; j < len; j++) {
    for (let i = j - 1; i >= 0; i--) {
      dp[i][j] = Math.max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
    }
  }
  return dp[0][len - 1] > 0;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

运行结果

石子是奇数，堆数是偶数，那么先手必赢。

所以，此题还有一种解法：

/**
 * @param {number[]} piles
 * @return {boolean}
 */
var stoneGame = function (piles) {
  // 直接返回 true
  return true;
};
1
2
3
4
5
6
7
8