【LeetCode】221. 最大正方形

题目描述

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例 1：

输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4

示例 2：

输入：matrix = [[“0”,“1”],[“1”,“0”]]
输出：1

示例 3：

输入：matrix = [[“0”]]
输出：0

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 ‘0’ 或 ‘1’

方法一：动态规划

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        // rows矩阵行数，cols矩阵列数 
        int rows=matrix.size(), cols=matrix[0].size();
        if(rows == 0 || cols == 0)  return 0;
        // maxSide 最大边长
        int maxSide = 0;
        // 相当于已经预处理完，使得第一行和第一列都为0
        vector<vector<int>> dp(rows+1, vector<int>(cols+1));

        for(int i=0; i<rows; i++){
            for(int j=0; j<cols; j++){
                if(matrix[i][j] == '1'){
                    dp[i+1][j+1] = min(min(dp[i][j], dp[i+1][j]), dp[i][j+1]) + 1;
                    maxSide = max(maxSide, dp[i+1][j+1]);
                }
            }
        }
        return pow(maxSide, 2);

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

心得

• 这道题我一开始用了暴力解法，嵌套了至少三个循环，写了好久好不容易能过测试点，最后提交的时候还是超时了，因此这里就不把我丑陋的代码放上来。

---

• 查看了题解，用了动态规划
• 重点：min(上, 左, 左上) + 1，也就是说，若某格子值为 1，则以此为右下角的正方形的、最大边长为：上面的正方形、左面的正方形或左上的正方形中，最小的那个，再加上此格。
• dp 具体定义：dp[i+1][j+1] 表示 「以第 i 行、第 j 列为右下角的正方形的最大边长」
  为什么不定义dp[i][j]呢，因为为了方便计算，我们在matrix的上面和左边加了一行‘0’值。
  因为任何一个正方形，我们都「依赖」当前格 左、上、左上三个方格的情况，但第一行的上层已经没有格子，第一列左边已经没有格子，这样就需要做另外的判断。
  
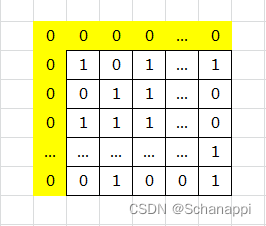
• 此时 dp 数组的大小也明确为 new dp[height + 1][width + 1]
  初始值就是将第一列 dp[row][0] 、第一行 dp[0][col] 都赋为 0，相当于已经计算了所有的第一行、第一列的 dp 值
  题目要求面积。根据 「面积 = 边长 x 边长」可知，我们只需求出 最大边长 即可，返回最大边长的平方就得到面积。
• 时间复杂度：O(cols * rows)
  空间复杂度：O(cols* rows)
• 这个解法可以进一步优化，但我现在的水平还没办法掌握，之后可以补一下，化二维为一维

[1]参考题解