（七）Java算法：希尔插入排序（详细图解）

一、前言

  希尔插入排序是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本，但是希尔排序是非稳定排序算法。
  希尔插入排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。

二、maven依赖

pom.xml

<dependencies>
    <dependency>
        <groupId>org.springframework.bootgroupId>
        <artifactId>spring-boot-starterartifactId>
        <version>2.6.0version>
    dependency>

    <dependency>
        <groupId>org.projectlombokgroupId>
        <artifactId>lombokartifactId>
        <version>1.16.14version>
    dependency>
dependencies>
1
2
3
4
5
6
7
8
9
10
11
12
13

三、编码实现

3.1、代码实现

  希尔插入排序的基本的实现（详细日志版）。

    /**
     * 希尔排序
     *
     * @param arr
     */
    public static void shellSort(int[] arr) {
        // 数组的长度
        int len = arr.length;
        log.info("数组的长度为：{}", len);
        // 定义间距
        int gap = len / 2;
        // 间距大于零就进行遍历
        while (gap > 0) {
            log.info("------------------------间距为【{}】时---------------------------", gap);
            // 从增量组开始
            for (int i = gap; i < len; i++) {
                // 待插入的数据
                int insertValue = arr[i];
                // 要插入的位置
                int j = i;
                log.info("第【{}】组元素是：【arr[{}]-->{}】和【arr[{}]-->{}】,要插入的值【{}】", (i - gap) + 1, j - gap, arr[j - gap], j, arr[j], insertValue);
                // 一组中从后往前遍历，条件是索引大于零并且要插入的值比前面索引对应的值还要小，就把当前组中的元素往后移动(可以去了解下直接插值排序)
                if (arr[j] < arr[j - gap]) {
                    log.info("本组中后面的值【{}】小于它前面的值【{}】", arr[j], arr[j - gap]);
                    while (j - gap >= 0 && insertValue < arr[j - gap]) {
                        log.info("要插入的值【{}】小于它前面的值【{}】", insertValue, arr[j - gap]);
                        log.info("【arr[{}]-->{}】移动到【arr[{}]-->{}】的位置,同时改变j的值为【{}】", j - gap, arr[j - gap], i, insertValue, j - gap);
                        // 把arr[j - gap]移动到arr[j]
                        arr[j] = arr[j - gap];
                        // 索引往前移动
                        j = j - gap;
                    }
                    log.info("最终待插入数据【{}】插入到索引为【{}】的位置", insertValue, j);
                    // 把值插入到指定位置
                    arr[j] = insertValue;
                } else {
                    log.info("本组中后面的值【{}】大于它前面的值【{}】", insertValue, arr[j - gap]);
                    log.info("最终待插入数据【{}】位置不变", insertValue);
                }
                log.info("第【{}】组排序后的结果：{}", (i - gap) + 1, arr);
                log.info("------------------------------");
            }
            // 再次缩小间距
            gap = gap / 2;
        }
    }

    public static void main(String[] args) {
        int[] arr = new int[]{28, 8, 10, 23, 21, 19, 9};
        log.info("要排序的初始化数据：{}", arr);
        //从小到大排序
        shellSort(arr);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

运行结果：

要排序的初始化数据：[28, 8, 10, 23, 21, 19, 9]
数组的长度为：7
------------------------间距为【3】时---------------------------
第【1】组元素是：【arr[0]-->28】和【arr[3]-->23】,要插入的值【23】
本组中后面的值【23】小于它前面的值【28】
要插入的值【23】小于它前面的值【28】
【arr[0]-->28】移动到【arr[3]-->23】的位置,同时改变j的值为【0】
最终待插入数据【23】插入到索引为【0】的位置
第【1】组排序后的结果：[23, 8, 10, 28, 21, 19, 9]
------------------------------
第【2】组元素是：【arr[1]-->8】和【arr[4]-->21】,要插入的值【21】
本组中后面的值【21】大于它前面的值【8】
最终待插入数据【21】位置不变
第【2】组排序后的结果：[23, 8, 10, 28, 21, 19, 9]
------------------------------
第【3】组元素是：【arr[2]-->10】和【arr[5]-->19】,要插入的值【19】
本组中后面的值【19】大于它前面的值【10】
最终待插入数据【19】位置不变
第【3】组排序后的结果：[23, 8, 10, 28, 21, 19, 9]
------------------------------
第【4】组元素是：【arr[3]-->28】和【arr[6]-->9】,要插入的值【9】
本组中后面的值【9】小于它前面的值【28】
要插入的值【9】小于它前面的值【28】
【arr[3]-->28】移动到【arr[6]-->9】的位置,同时改变j的值为【3】
要插入的值【9】小于它前面的值【23】
【arr[0]-->23】移动到【arr[6]-->9】的位置,同时改变j的值为【0】
最终待插入数据【9】插入到索引为【0】的位置
第【4】组排序后的结果：[9, 8, 10, 23, 21, 19, 28]
------------------------------
------------------------间距为【1】时---------------------------
第【1】组元素是：【arr[0]-->9】和【arr[1]-->8】,要插入的值【8】
本组中后面的值【8】小于它前面的值【9】
要插入的值【8】小于它前面的值【9】
【arr[0]-->9】移动到【arr[1]-->8】的位置,同时改变j的值为【0】
最终待插入数据【8】插入到索引为【0】的位置
第【1】组排序后的结果：[8, 9, 10, 23, 21, 19, 28]
------------------------------
第【2】组元素是：【arr[1]-->9】和【arr[2]-->10】,要插入的值【10】
本组中后面的值【10】大于它前面的值【9】
最终待插入数据【10】位置不变
第【2】组排序后的结果：[8, 9, 10, 23, 21, 19, 28]
------------------------------
第【3】组元素是：【arr[2]-->10】和【arr[3]-->23】,要插入的值【23】
本组中后面的值【23】大于它前面的值【10】
最终待插入数据【23】位置不变
第【3】组排序后的结果：[8, 9, 10, 23, 21, 19, 28]
------------------------------
第【4】组元素是：【arr[3]-->23】和【arr[4]-->21】,要插入的值【21】
本组中后面的值【21】小于它前面的值【23】
要插入的值【21】小于它前面的值【23】
【arr[3]-->23】移动到【arr[4]-->21】的位置,同时改变j的值为【3】
最终待插入数据【21】插入到索引为【3】的位置
第【4】组排序后的结果：[8, 9, 10, 21, 23, 19, 28]
------------------------------
第【5】组元素是：【arr[4]-->23】和【arr[5]-->19】,要插入的值【19】
本组中后面的值【19】小于它前面的值【23】
要插入的值【19】小于它前面的值【23】
【arr[4]-->23】移动到【arr[5]-->19】的位置,同时改变j的值为【4】
要插入的值【19】小于它前面的值【21】
【arr[3]-->21】移动到【arr[5]-->19】的位置,同时改变j的值为【3】
最终待插入数据【19】插入到索引为【3】的位置
第【5】组排序后的结果：[8, 9, 10, 19, 21, 23, 28]
------------------------------
第【6】组元素是：【arr[5]-->23】和【arr[6]-->28】,要插入的值【28】
本组中后面的值【28】大于它前面的值【23】
最终待插入数据【28】位置不变
第【6】组排序后的结果：[8, 9, 10, 19, 21, 23, 28]
------------------------------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

3.2、精简日志版

  去掉多余的日志。

public static void shellSortNolog(int[] arr) {
        // 数组的长度
        int len = arr.length;
        // 定义间距
        int gap = len / 2;
        // 间距大于零就进行遍历
        while (gap > 0) {
            log.info("------------------------间距为【{}】时---------------------------", gap);
            // 从增量组开始
            for (int i = gap; i < len; i++) {
                // 待插入的数据
                int insertValue = arr[i];
                // 要插入的位置
                int j = i;
                // 一组中从后往前遍历，条件是索引大于零并且要插入的值比前面索引对应的值还要小，就把当前组中的元素往后移动(可以去了解下直接插值排序)
                if (arr[j] < arr[j - gap]) {
                    while (j - gap >= 0 && insertValue < arr[j - gap]) {
                        // 把arr[j - gap]移动到arr[j]
                        arr[j] = arr[j - gap];
                        // 索引往前移动
                        j = j - gap;
                    }
                    // 把值插入到指定位置
                    arr[j] = insertValue;
                }
                log.info("第【{}】组排序后的结果：{}", (i - gap) + 1, arr);
            }
            // 再次缩小间距
            gap = gap / 2;
        }
    }

    public static void main(String[] args) {
        int[] arr = new int[]{28, 8, 10, 23, 21, 19, 9};
        log.info("要排序的初始化数据：{}", arr);
        //从小到大排序
        shellSort(arr);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

运行结果：

要排序的初始化数据：[28, 8, 10, 23, 21, 19, 9]
------------------------间距为【3】时---------------------------
第【1】组排序后的结果：[23, 8, 10, 28, 21, 19, 9]
第【2】组排序后的结果：[23, 8, 10, 28, 21, 19, 9]
第【3】组排序后的结果：[23, 8, 10, 28, 21, 19, 9]
第【4】组排序后的结果：[9, 8, 10, 23, 21, 19, 28]
------------------------间距为【1】时---------------------------
第【1】组排序后的结果：[8, 9, 10, 23, 21, 19, 28]
第【2】组排序后的结果：[8, 9, 10, 23, 21, 19, 28]
第【3】组排序后的结果：[8, 9, 10, 23, 21, 19, 28]
第【4】组排序后的结果：[8, 9, 10, 21, 23, 19, 28]
第【5】组排序后的结果：[8, 9, 10, 19, 21, 23, 28]
第【6】组排序后的结果：[8, 9, 10, 19, 21, 23, 28]
1
2
3
4
5
6
7
8
9
10
11
12
13

四、运行流程

4.1、第一轮

  第一轮的初始数据是：28, 8, 10, 23, 21, 19, 9，数组的长度是7，在希尔插入排序中，我们计算间距方式是：gap=数组长度/2 =7/2 = 3，在本程序中，上面的数组我们在逻辑上两两一组：arr[0]和arr[3]、arr[1]和arr[4]、arr[2]和arr[5]、arr[3]和arr[6]，可能有小伙伴就会有不同的意见认为：arr[0]、arr[3]和arr[6]是一组，他们的间距都是3，符合分组条件，说法也是没有错的，原因我到第一轮第四组排序时再说。

4.1.1、第一组

  从上面分析得知，我们第一组的数据是：arr[0]和arr[3]，我们需要对这两个数进行插入排序。我们得到：

• 待插入数：arr[3]，也就是23
• 实际待插入列表：arr[0]、arr[3]

• 待插入数23比arr[0]（也就是28）小，所以arr[0]移动到arr[3]
• 待插入数23插入到arr[0]的位置

  很多小伙伴就迷惑了，为什么是减去3？因为希尔排序规定先按间距分组，然后对每一组进行插入排序，然后不断缩写间距到1，完成最后的排序。而我们之前计算的间距：gap=数组长度/2 =7/2 = 3，插入排序时一般是用后面一个数和前面的有序列表进行比较，找到插入的位置，然后插入数据。一般插入排序是从第二个数往前插入，所以我们初始位置是一个间距的位置arr[j]=arr[gap]=arr[3]，往前一个数就是arr[j-gap]=arr[3-3]=0，你一定要先搞懂这个。

4.1.2、第二组

  同理，我们第二组的数据是：arr[1]和arr[4]，我们需要对这两个数进行插入排序。需要注意的是：初始数据是第一轮第一组排序后的数据。我们得到：

• 待插入数：arr[4]，也就是21
• 实际待插入列表：arr[1]、arr[4]
  
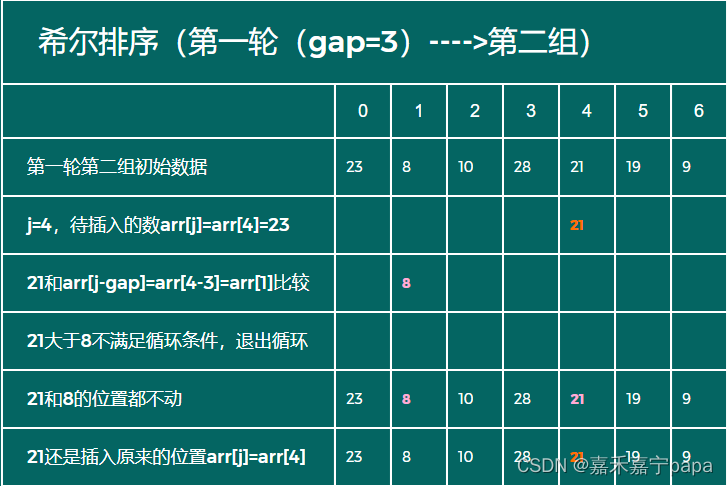
• 待插入数21比arr[1]（也就是8）大，所以arr[1]和arr[4]位置不动
• 待插入数23还是插入到原来arr[4]的位置

4.1.3、第三组

  同理，我们第三组的数据是：arr[2]和arr[5]，我们需要对这两个数进行插入排序。需要注意的是：初始数据是第一轮第二组排序后的数据。我们得到：

• 待插入数：arr[5]，也就是19
• 实际待插入列表：arr[2]、arr[5]

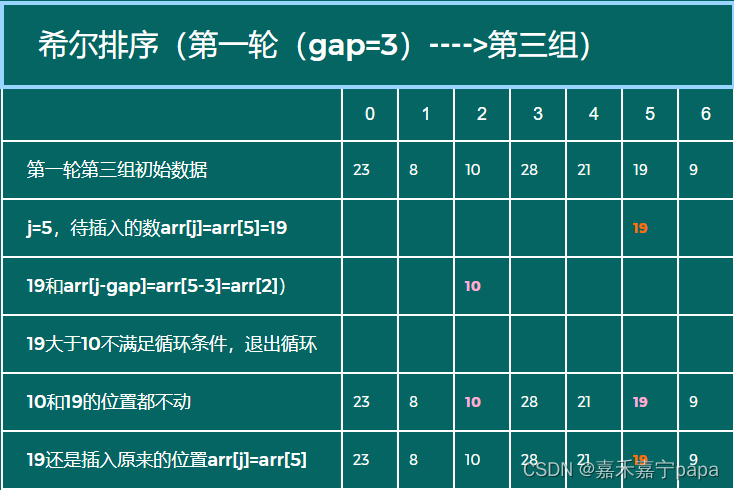
• 待插入数19比arr[2]（也就是10）大，所以arr[2]和arr[5]位置不动
• 待插入数19还是插入到原来arr[5]的位置

4.1.4、第四组

  同理，我们第四组的数据是：arr[3]和arr[6]，我们需要对这两个数进行插入排序。需要注意的是：初始数据是第一轮第三组排序后的数据。我们得到：

• 待插入数：arr[6]，也就是9
• 实际待插入列表：arr[0]、arr[3]、arr[6]

• 待插入数9比arr[3]（也就是28）小，所以arr[3]移动到arr[6]的位置
• 待插入数9比arr[0]（也就是23）小，所以arr[0]移动到arr[3]的位置
• 待插入数9插入到arr[0]的位置

  经过第四组排序arr[0]、arr[3]、arr[6]这三个数（不看其他数）它们已经是有序的了（本文是升序排序）。

  对于前面的疑惑我们做一个答疑，我们把arr[0]、arr[3]分成一个逻辑组，arr[3]、arr[6]分成一个逻辑组，并没有把arr[0]、arr[3]、arr[6]分成一个逻辑组。我们再来看下直接插入排序的概念。直接插入排序基本思想是将一个记录插入到已经排好序的有序列表中。是的你没看错，将一个数插入一个列表，该列表一定要是有序的。

  如果arr[0]、arr[3]、arr[6]分成一个逻辑组，然后从arr[3]开始去插入，那么就要先把arr[0]、arr[3]排序完，再插入arr[6]，相当于你希尔插入排序再嵌入直接插入排序了，在那么算法的复杂度上升一个台阶，实现的思路不就是我们两两分组做法是一样的么。我们将arr[0]和arr[3]分成一组，经历过直接插入排序（第一轮第一组），此列表一定是有序的（本文是arr[0]一定小于等于arr[3]），此时arr[6]插入就没有问题了，同样完成了arr[0]、arr[3]、arr[6]列表的排序。

  这种情况一般是列表的个数是奇数才会现在一个列表有3个元素，偶数列表是不会出现，就以本文来说，列表个数是奇数7，arr[0]、arr[3]和arr[6]是一个列表的，你也可以说是一个组，但是我们处理时，一定是先把前面两个数（arr[0]、arr[3]）处理成有序列表，然后arr[6]再插入到有序列表中。

4.2、第二轮

  第二轮的初始数据是第一轮第四组排序后的数据：9, 8, 10, 23, 21, 19, 28，在之前的间距基础上，我们继续缩写间距：gap=gap/2 =3/2 = 1，在本程序中，上面的数组继续变成两两一组：arr[0]和arr[1]、arr[1]和arr[2]、arr[2]和arr[3]、arr[3]和arr[4]、arr[4]和arr[5]、arr[5]和arr[6]。

4.1.1、第一组

  从上面分析得知，我们第二轮第一组的数据是：arr[0]和arr[1]，我们需要对这两个数进行插入排序。经过第一轮第四组解答，我们知道：

• 待插入数：arr[1]，也就是8
• 实际待插入列表：arr[0]、arr[1]

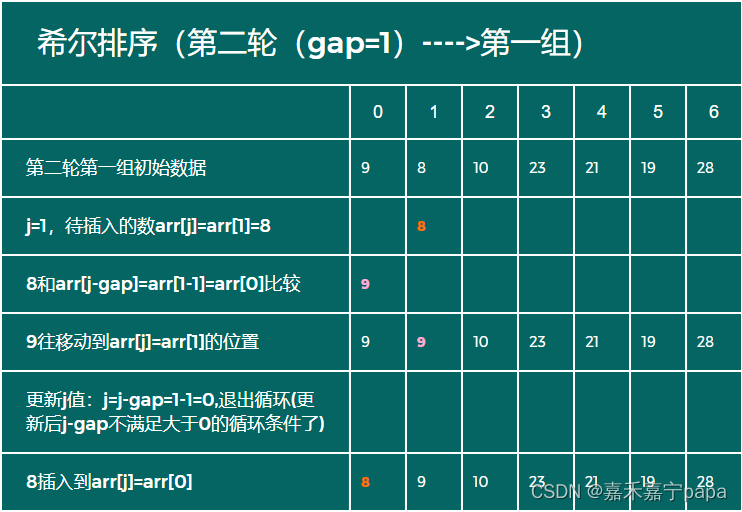
• 待插入数8比arr[0]（也就是9）小，所以arr[0]移动到arr[1]
• 待插入数8插入到arr[0]的位置

4.1.2、第二组

  同理，我们第二轮第二组的数据是：arr[1]和arr[2]，需要注意的是：初始数据是第二轮第一组排序后的数据。经过第一轮第四组解答，我们知道：

• 待插入数：arr[2]，也就是10
• 实际待插入列表：arr[0]、arr[1]、arr[2]
  
• 待插入数10比arr[1]（也就是9）都大，所以arr[0]、arr[1]、arr[2]列表元素都不动。（因为经过前面一组排序，arr[0]和arr[1]一定是有序列表，不用继续与arr[0]比较了）
• 待插入数10还是插入到原来的位置arr[2]

4.1.3、第三组

  同理，我们第二轮第三组的数据是：arr[2]和arr[3]，需要注意的是：初始数据是第二轮第二组排序后的数据。待处理信息如下：

• 待插入数：arr[3]，也就是23
• 实际待插入列表：arr[0]、arr[1]、arr[2]、arr[3]

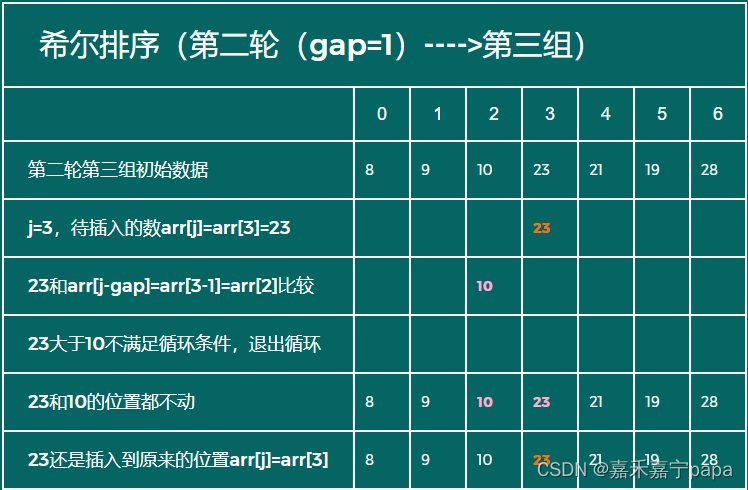
• 待插入数23比arr[2]（也就是10）都大，所以arr[0]、arr[1]、arr[2]、arr[3]列表元素都不动。（因为经过前面一组排序，arr[0]、arr[1]、arr[2]一定是有序列表，不用继续与arr[2]前面的元素比较了）
• 待插入数10还是插入到原来的位置arr[2]

4.1.4、第四组

  同理，我们第二轮第四组的数据是：arr[3]和arr[4]，需要注意的是：初始数据是第二轮第三组排序后的数据。待处理信息如下：

• 待插入数：arr[4]，也就是21
• 实际待插入列表：arr[0]、arr[1]、arr[2]、arr[3]、arr[4]

• 待插入数21比arr[3]（也就是23）小，所以arr[3]移动到arr[4]的位置
• 待插入数21比arr[2]（也就是10）大，所以arr[0]、arr[1]、arr[2]列表元素都不动。（因为经过前面一组排序，arr[0]、arr[1]、arr[2]一定是有序列表，不用继续与arr[2]前面的元素比较了），
• 待插入数21插入到arr[3]的位置

4.1.5、第五组

  同理，我们第二轮第五组的数据是：arr[4]和arr[5]，需要注意的是：初始数据是第二轮第四组排序后的数据。待处理信息如下：

• 待插入数：arr[5]，也就是19
• 实际待插入列表：arr[0]、arr[1]、arr[2]、arr[3]、arr[4]、arr[5]

• 待插入数19比arr[4]（也就是23）小，所以arr[4]移动到arr[5]的位置
• 待插入数19比arr[3]（也就是21）小，所以arr[3]移动到arr[4]的位置
• 待插入数19比arr[2]（也就是10）大，所以arr[0]、arr[1]、arr[2]列表元素都不动（因为经过前面一组排序，arr[0]、arr[1]、arr[2]一定是有序列表，不用继续与arr[2]前面的元素比较了）
• 待插入数19插入到arr[3]的位置

4.1.6、第六组

  同理，我们第二轮第五组的数据是：arr[5]和arr[6]，需要注意的是：初始数据是第二轮第五组排序后的数据。待处理信息如下：

• 待插入数：arr[6]，也就是28
• 实际待插入列表：arr[0]、arr[1]、arr[2]、arr[3]、arr[4]、arr[5]、arr[6]

• 待插入数28比arr[5]（也就是23）都大，所以arr[0]、arr[1]、arr[2]、arr[3]、arr[4]、arr[5]、arr[6]列表元素都不动。（因为经过前面一组排序，arr[0]、arr[1]、arr[2]、arr[3]、arr[4]一定是有序列表，不用继续与arr[5]前面的数比较了）
• 待插入数28还是插入到原来的位置arr[6]

结语

  要想掌握希尔插入排序，一定要先了解直接插入排序，因为希尔插入排序就是直接插入排序的一种改良方式，只不过不是很稳定，我们现在讲了三种插入排序了：

• 直接插入排序
• 二分插入排序
• 希尔插入排序

  但是不管哪一种方式，它们在插入一个数的时候，一定要先确保，当前插入数之前的列表是有序的，如果这点没想清楚，那么这三个算法就理解不了的。当有奇数个列表时，比如三个，我们把它们拆成两组即可。