大数据算法系列11:线性规划

一. 线性规划问题的数学模型

1.1 例子

1.1.1 例1

设四个角截去的小正方形边长为X.
则有盒子的体积为:
$V=(a-2X）\ast (a-2X)\ast X=a^{2}X-4a{X}^2+4X^3$

$V’=a^2-8aX+12X^2=(a-2X)\ast (a-6X)$
令V’=0得:X1=a/2； X2=a/6
又:V”= -8a+24X
当X1=a/2时,V”= 4a＞0,V有极小值0；
当X2=a/6时,V”= -4a＜0,V有极大值：
V极大=(2/27)a^3

1.1.2 例2

1.1.3 例3

例3区别于例1和例2，已经转换为了标准的数学公式

1.1.4 例4

通过矩阵来求最优解

1.2 线性规划的数学模型概要

三要素:

二. 线性规划的解

求解方法
图解法有点类似几何的解法
单纯形法有点类似代数的解法

2.1 图解法

2.2 单纯形法

2.2.1 基本原理

2.2.2 从一个简单例子入手

2.3 解的类型

2.3.1 初始基本可行解的确定

最优性检验:

总结计算步骤:

2.3.2 例子

四. 线性规划模型的应用

4.1 案例:公交车司机

4.2 案例:生产计划问题

4.3 案例:套载下料问题

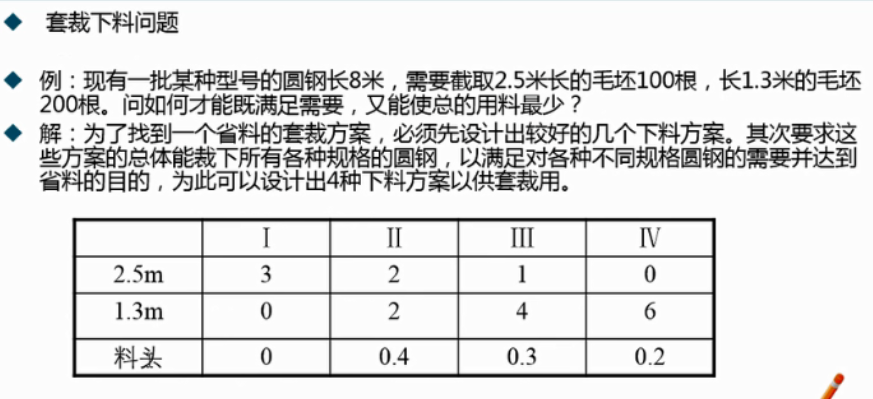
目标函数:
Min x1 + x2 + x3 + x4

约束条件:
3x1 + 2x2 + 3x3 + 0x4 >= 100
0x1 + 2x2 + 4x3 + 6x3 >= 200
x1,x2,x3,x4 >= 0

参考:

1. http://www.dataguru.cn/article-5747-1.html