八大排序之插入排序

目录

一 插入排序

日常生活

基本思想

图解

代码

分析

二 希尔排序

产生

两种确定gap的方法

希尔排序的两种思想

有一种思路

第二种思路

代码

三 总结

插入排序

希尔排序

---

一 插入排序

日常生活

我们日常生活中玩斗地主的时候，整理手牌也是按照这个思想来进行整理的

基本思想

插入排序的基本思想是：假设有一个数组是无序的数组，以从前往后排序为例子，排升序

一个数据可以认为是已经有序的，那么第二个数据插入的时候与之前的数据进行比较，如果比之前的数据小，那么这个之前的数据就要往后移动一个位置

由于往后移动一个位置挤占掉新插入的这个数据的位置，因此就需要创建一个临时变量tmp，将他的值保存起来，将tmp和之前的数据依次进行比较，直到碰到比他大的数据，就插入在这个数据的后面

图解

 

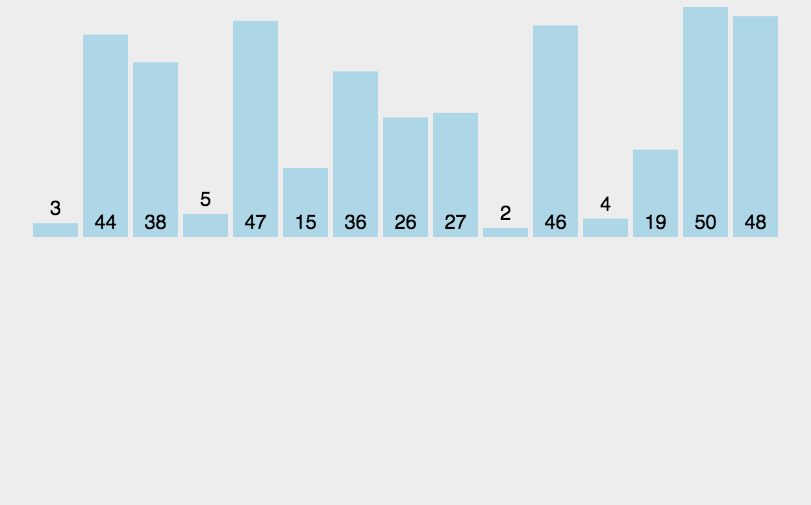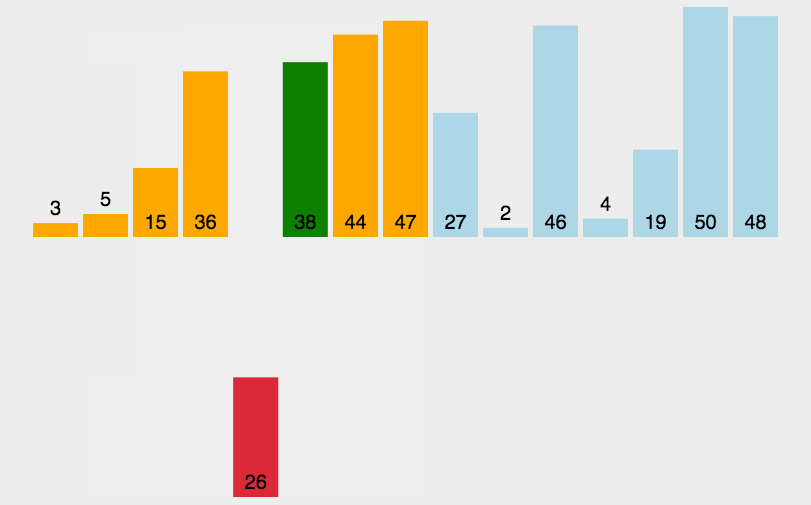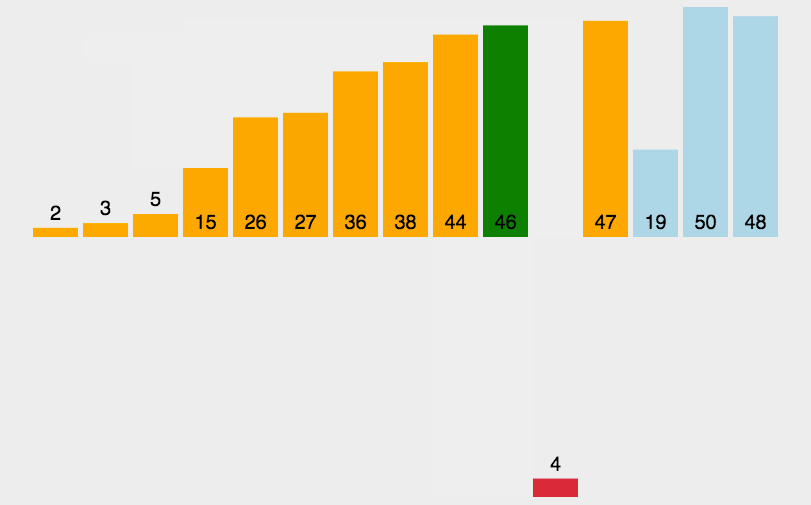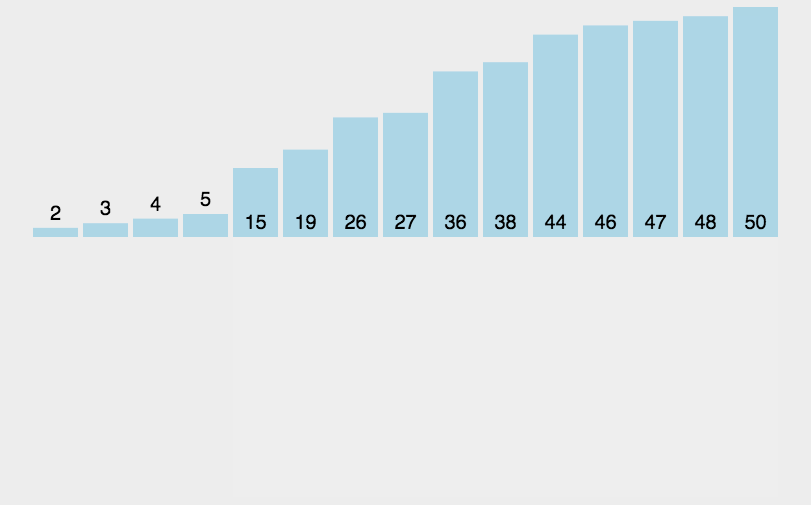
代码

void InsertSort(int* a, int n)
{
	assert(a);
	for (int i = 0; i < n-1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

分析

插入排序比较适合有序或者接近有序的数列，这样他在排序的时候会比较快，但是如果一个序列是逆序的，那么此时插入排序的时间复杂度就是O（n^2),相对来说的话就比较慢了。有没有什么可以改进的地方呢？

改进：由于插入排序的低效是由于数据无序或者逆序造成的，那么我们有没有办法将这样一个无序的数列变得有序或者接近有序以提高排序的速度呢？

这里就引入了希尔排序

二 希尔排序

产生

希尔排序是基于插入排序产生的，希尔排序可以提高插入排序的速度，相当于对插入排序的一个优化。

这里用的一个基本思想是预排序：也就是说对一个随机的数列先进行插入排序，只不过这个插入排序的间隔gap由自己确定。如果gap比较大的话，那么相对的，较小的数据能较快的到达后面（排升序为例子），gap较小的话，能排的更多，数列更接近有序，但是消耗也比较大。所以gap的确定是一个很重要的点。

将他排成一个相对有序的数列之后再用一次间隔为1的插入排序，那么整体就排好了。

预排序中最主要的还是gap的确定。

两种确定gap的方法

①gap/=3+1;

gap每次变化是之前的三分之一，由于最后一次可能为0，为了保证他一定能够取到1，因此最后需要+1

②gap/=2

这样的话能保证最后一次一定是1，但是变化的速度稍微会慢

希尔排序的两种思想

假设gap选取第一种，我们进行希尔排序：

有一种思路

随着gap的变化，每一次分组会发生变化，对这些组都按照gap进行排序。相当于红色排好之后排黄色，黄色排好之后排蓝色，蓝色排好之后排绿色

第二种思路

随着gap的变化，虽然每一次分组确实也会发生变化，但是这些组之间仍然间隔1来排序。为啥这样是可行的呢？这里其实有个取巧了，相当于依次对红黄蓝绿进行第一次预排序，完了之后继续对红黄蓝绿进行第二次预排序，等循环结束的时候，刚好每个颜色的组都被排到了

以上只对第一次取得gap进行预排序了，之后其实差不多，经过多次预排序之后得到的就是一个有序或者接近有序的数列了

代码

void ShellSort(int* a, int n)
{
	assert(a);
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)//for (int i = 0; i < n-gap; i+=gap)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end-= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}//插入排序

三 总结

希尔排序和插入排序的思想都是差不多的，都是利用插入的思想进行排序的。只不过希尔排序是在插入排序的思想上进行的一个优化。

插入排序

插入排序的适应性比较强，适合于随机，相对有序的数列

插入排序的稳定性也是比较强的，他不会改变元素的相对位置，一次插入排序就排出来了

时间复杂度：O（n^2)

空间复杂度：O（1）

希尔排序

希尔排序是对插入排序的一个优化，她的效率会比较高

但是希尔排序的稳定性较差，一次插入排序不会对元素的相对位置进行改变，但是多次插入排序就会打乱元素的相对位置，因此稳定性较差

时间复杂度：O（N^1.3）.她的计算比较复杂，跟gap的取值有关。

空间复杂度：O（1）