背包问题详解（含代码）

前两天组长让我给社团的新生们出些简单的C++题目，然后他让我出些算法题。然后我就从《趣学算法》里面找了两道题（自己出题实在是折磨人），其中就有背包问题。

在之前看到的一篇文章《背包问题九讲》里，把背包问题系统分成了九类，分别是：背包问题、完全背包问题、多重背包问题、混合三种背包问题，二维费用的背包问题，分组的背包问题，有依赖的背包问题，泛化物品的背包问题以及其他背包问题。

在这里，结合《趣学算法》中的背包问题进行基础的复习以及思考，简单介绍一下，部分背包，01背包，完全背包以及多重背包。

---

一、部分背包问题

题目：

有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的空间是 Ci，得到的价值是 Wi，物品可以分割。求解将哪些物品装入背包可使价值总和最大。

基本思路：贪心

该题特点：物品可以分割

举例说明：在《趣学算法》里，有这样一个问题
假设山洞中有 n 种宝物，每种宝物有一定重量 w 和相应的价值 v，毛驴运载能力有限，只能运走 m 重量的宝物，一种宝物只能拿一样，宝物可以分割。那么怎么才能使毛驴运走宝物的价值最大呢？

可以看到，宝物可以分割。也就是说，我们可以每次都选择单位体积价值最高的物品，这样达到运载上限的时候，运载物品的价值也最高，也是就计算物品的性价比序列。

#include 
#include 
using namespace std;
const int M = 1000005;
struct three {
	double w;//每个宝物的重量
	double v;//每个宝物的价值
	double p;//性价比
}s[M];
bool cmp(three a, three b)
{
	return a.p > b.p;//根据宝物的单位价值从大到小排序
}
int main()
{
	int n;//n 表示有 n 个宝物
	double m;//m 表示毛驴的承载能力
	cout << "请输入宝物数量 n 及毛驴的承载能力 m ：" << endl;
	cin >> n >> m;
	cout << "请输入每个宝物的重量和价值，用空格分开： " << endl;
	for (int i = 0; i < n; i++)
	{
		cin >> s[i].w >> s[i].v;
		s[i].p = s[i].v / s[i].w;//每个宝物单位价值
	}
	sort(s, s + n, cmp);
	double sum = 0.0;// sum 表示贪心记录运走宝物的价值之和
	for (int i = 0; i < n; i++)//按照排好的顺序贪心
	{
		if (m > s[i].w)//如果宝物的重量小于毛驴剩下的承载能力
		{
			m -= s[i].w;
			sum += s[i].v;
		}
		else//如果宝物的重量大于毛驴剩下的承载能力
		{
			sum += m * s[i].p;//部分装入
			break;
		}
	}
	cout << "装入宝物的最大价值 Maximum value=" << sum << endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

除了这种既要考虑体积又要考虑价值的背包问题，还有一种更简单的最优装载问题，也适合使用贪心算法。

例如：有一天，海盗们截获了一艘装满各种各样古董的货船，每一件古董都价值连城，一旦打碎就失去了它的价值。虽然海盗船足够大，但载重量为 C，每件古董的重量为 wi，海盗们该如何把尽可能多数量的宝贝装上海盗船呢？

这种问题只需要考虑到物品的体积（重量）而不需要考虑其价值，所以优先把重量小的物品放进去，在容量固定的情况下，装的物品最多。

#include  
#include  
const int N = 1000005;
using namespace std;
double w[N]; //古董的重量数组
int main()
{
	double c;
	int n;
	cout << "请输入载重量 c 及古董个数 n：" << endl;
	cin >> c >> n;
	cout << "请输入每个古董的重量，用空格分开： " << endl;
	for (int i = 0; i < n; i++)
	{
		cin >> w[i]; //输入每个物品重量
	}
	sort(w, w + n); //按古董重量升序排序
	double tmp = 0.0;
	int ans = 0; // tmp 为已装载到船上的古董重量，ans 为已装载的古董个数 
	for (int i = 0; i < n; i++)
	{
		tmp += w[i];
		if (tmp <= c)
			ans++;
		else
			break;
	}
	cout << "能装入的古董最大数量为 Ans=";
	cout << ans << endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

二、01背包问题

题目

有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的空间是 Ci，得到的价值是 Wi。求解将哪些物品装入背包可使价值总和最大。

基本思路

该题特点：每种物品仅有一个，可以选择放或者不放。也就是0（不放入）和1（放入）这两种状态

一般来说，01背包有三种解法：

• 暴力算法：思路简单，找到所有物品的组合，进行计算，推出最优解
• 贪心算法：其实这个算法是适合部分背包问题（物品可分割的装载问题我们称为部分背包问题），而在01背包问题（物品不可分割的装载问题）这里，求出来的只能是最优解的近似解，并不准确
• dp动态规划：解决01背包问题，当然也可以说，解决所有背包问题（几乎所有背包问题都可以转变为01背包问题），可以求出最优解

1、暴力解法

假设有n个物体，价值和重量分别用vi和wi来表示，用暴力搜索，我们将最终的解用一个向量来表示，因此所有的解空间可以用00…00到11…11来表示。而这些数恰对应0至2^n-1的二进制转换。因此可以基于该思想，利用二进制转换进行暴力搜索。

    #include   
    #include   
      
    int main()  
    {  
        int num,maxv=0;  
        int n, c, *w, *v, tempw, tempv;  
        int i,j,k;  
      
        printf("input the number and the volume:");  
        scanf("%d%d",&n,&c);  
          
        w=new int [n];  
        v=new int [n];  
      
      
        printf("input the weights:");  
        for(i=0;i<n;i++)  
            scanf("%d",&w[i]);  
      
        printf("input the values:");  
        for(i=0;i<n;i++)  
            scanf("%d",&v[i]);  
      
        for(num=0;num<pow(2,n);num++) //每一个num对应一个解  
        {  
            k=num; tempw=tempv=0;     
            for(i=0;i<n;i++) //n位二进制  
            {  
                if(k%2==1){     //如果相应的位等于1，则代表物体放进去，如果是0，就不用放了  
                    tempw+=w[i];  
                    tempv+=v[i];  
                }  
                k=k/2;          //二进制转换的规则  
            }  
            //循环结束后，一个解空间生成，  
            //判断是否超过了背包的容积，  
            //如果没有超，判断当前解是否比最优解更好  
            if(tempw<=c){  
                if(tempv>maxv)  
                    maxv=tempv;  
            }  
        }  
      
        printf("the result is %d.\n",maxv);  
      
        return 0;     
    }  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

暴力算法在解决数值量较少的问题上可以使用，但一旦数值量过大，可能出现耗时很长的问题。所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

2、贪心解法

贪心解法如上，虽然贪心解法适合部分背包问题。

但是，贪心算法不适合01背包问题。比如说，如下图所示：

如果我们采用贪心算法，先装性价比高的物品，且物品不能分割，剩余容量如果无法再装入剩余的物品，不管还有没有运载能力，算法都会结束。那么我们选择的物品为 1 和 2，总价值为 31，而实际上还有 3 个剩余容量，但不足以装下剩余其他物品，因此得到的最大价值为 31。但实际上我们如果选择物品 2 和 3，正好达到运载力，得到的最大价值为 34。也就是说，在物品不可分割、没法装满的情况下，贪心算法并不能得到最优解，仅仅是最优解的近似解。

3、动态规划(dp)

3.1 什么是动态规划

讲真，原理和概念很复杂，看了和没看是一样的，没看一脸懵逼，看完也还是云里雾里。在《算法图解》这本书里，虽然没有具体解释什么是动态规划，但是它采用了一系列动态规划的题目来让我们理解什么是动态规划，建议观看。

3.2 开始演算

用子问题定义状态：即F[i, v]表示前i件物品恰放入一个容量为v的背包可
以获得的最大价值。则其状态转移方程便是：

F [ i , v ] = m a x { F [ i − 1 , v ] , F [ i − 1 , v − C i ] + W i } F\left [ i ,v\right ]= max \left \{ F\left [ i-1,v \right ] ,F\left [ i-1 ,v-Ci\right ] + Wi\right \} F[i,v]=max{F[i−1,v],F[i−1,v−Ci]+Wi}

这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下：“将前i件物品放入容量为v的背包中”这个子问题，若只考虑第i件物品的策略（放或不放），那么就可以转化为一个只和前i − 1件物品相关的问题。如果不放第i件物品，那么问题就转化为“前i − 1件物品放入容量为v的背包中”，价值为F[i − 1, v]；如果放第i件物品，那么问题就转化为“前i − 1件物品放入剩下的容量为v − Ci的背包中”，此时能获得的最大价值就是F[i − 1, v − Ci]再加上通过放入第i件物品获得的价值Wi。

这里我觉得给出《趣学算法》里的一道题来解释，可能更好理解。

例题：假设现在有 5 个物品，每个物品的重量为（2，5，4，2，3），价值为（6，3，5，4，6），如图所示。购物车的容量为 10，求在不超过购物车容量的前提下，把哪些物品放入购物车，才能获得最大价值。

(记住这张图)

首先初始化：

c[i][j]表示前 i 件物品放入一个容量为 j 的购物车可以获得的最大价值。初始化 c[][]数组：0 行 0 列为 0：c[0][j]=0，c[i][0] =0，其中 i=0，1，2，…，n，j=0，1，2，…，W。
按照递归式计算第 1 个物品（i=1）的处理情况，得到：
c [ i ] [ j ] = { c [ i − 1 ] [ j ] , j < w i m a x { c [ i − 1 ] [ j ] , c [ i − 1 ] [ j − w [ i ] ] + v [ i ] } , j ≥ w i c\left [ i \right ]\left [ j \right ] = \left\{

\right. c[i][j]={c[i−1][j]max{c[i−1][j],c[i−1][j−w[i]]+v[i]}​,j<wi​,j≥wi​​​

构建网格：
每一个动态规划问题都是从一个网格开始的，如下：

处理数据，仔细看。

这样就可以得到第一行。

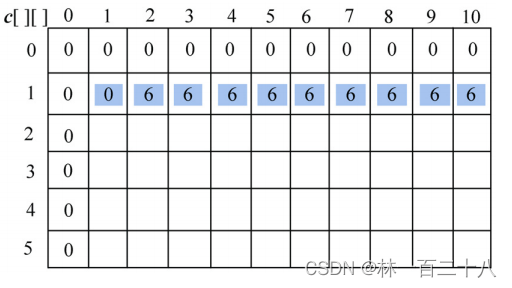
继续第二行。

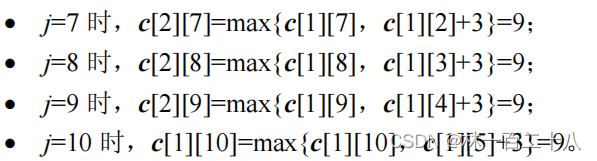
这样就又得到了一行。

按照这样的方法不断计算，就可以得到：

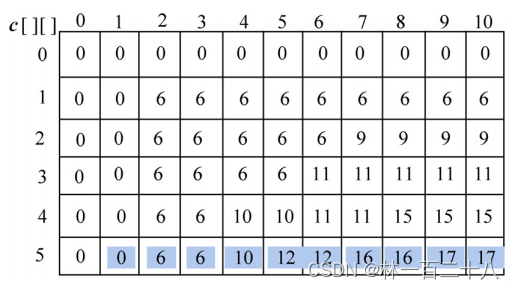
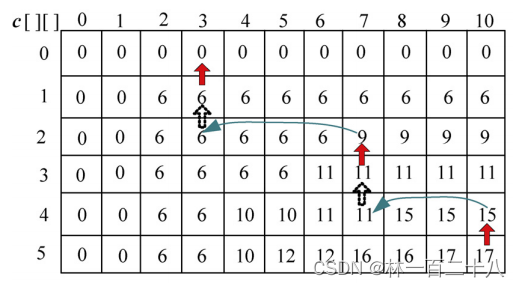
3.3 构造最优解

• 首先读取 c[5][10]>c[4][10]，说明第 5 个物品装入了购物车，即 x[5]=1，j=10−w[5]=7；
• 去找 c[4][7]=c[3][7]，说明第 4 个物品没装入购物车，即 x[4]=0；
• 去找 c[3][7]>c[2][7]，说明第 3 个物品装入了购物车，即 x[3]=1，j= j−w[3]=3；
• 去找 c[2][3]=c[1][3]，说明第 2 个物品没装入购物车，即 x[2]=0；
• 去找 c[1][3]>c[0][3]，说明第 1 个物品装入了购物车，即 x[1]=1，j= j−w[1]=1。
  

3.4 代码

#include  
#include 
using namespace std;
#define maxn 10005 
#define M 105 
int c[M][maxn]; //c[i][j] 表示前 i 个物品放入容量为 j 购物车获得的最大价值
int w[M], v[M]; //w[i] 表示第 i 个物品的重量，v[i] 表示第 i 个物品的价值
int x[M]; //x[i]表示第 i 个物品是否放入购物车
int main() {
	int i, j, n, W; //n 表示 n 个物品，W 表示购物车的容量
	cout << "请输入物品的个数 n：";
	cin >> n;
	cout << "请输入购物车的容量 W：";
	cin >> W;
	cout << "请依次输入每个物品的重量 w 和价值 v，用空格分开：";
	for (i = 1; i <= n; i++)
		cin >> w[i] >> v[i];
	for (i = 0; i <= n; i++) //初始化第 0 列为 0 
		c[i][0] = 0;
	for (j = 0; j <= W; j++) //初始化第 0 行为 0 
		c[0][j] = 0;
	for (i = 1; i <= n; i++) //计算 c[i][j] 
		for (j = 1; j <= W; j++)
			if (j < w[i]) //当物品的重量大于购物车的容量，则不放此物品
				c[i][j] = c[i - 1][j];
			else //否则比较此物品放与不放是否能使得购物车内的价值最大
				c[i][j] = max(c[i - 1][j], c[i - 1][j - w[i]] + v[i]);
	cout << "装入购物车的最大价值为：" << c[n][W] << endl;
	//逆向构造最优解

	j = W;
	for (i = n; i > 0; i--)
		if (c[i][j] > c[i - 1][j])
		{
			x[i] = 1;
			j -= w[i];
		}
		else
			x[i] = 0;
	cout << "装入购物车的物品为：";
	for (i = 1; i <= n; i++)
		if (x[i] == 1)
			cout << i << " ";
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

也许一个例题不能让你完全理解，那还可以看看这篇博客。

三、完全背包问题

完全背包问题就是在01背包问题的基础上加了一个条件：物品有无限个，可以无限使用。

题目：

有N种物品和一个容量为V 的背包，每种物品都有无限件可用。放入第i种物品的费用是Ci，价值是Wi。求解：将哪些物品装入背包，可使这些物品的耗费的费用总和不超过背包容量，且价值总和最大。

基本思路

该题特点：每一种物品都可以无限使用

思路一：转变为01背包问题

这也就是几乎所有背包问题都可以转变为01背包问题：装满容量为j的背包，重量为wi的物品顶多V/wi件。

F[i][j] = max(F[i-1][j-kwi] + kvi), 0<= k <=j/wi

伪代码

int weight[200], value[200], f[100], n, w;
void dp(){
    for (int i = 1; i <= n; i++)
	for (int j = w; j >= weight[i]; j--)
	      for (int k = 1; k * weight[i] <= j; k++)
		   f[j] = max(f[j], f[j - k*weight[i]] + k*value[i]);
}
1
2
3
4
5
6
7

思路二：F[i][j]表示从前i种物品中挑选总重量不超过j的物品的最大价值。

如果不取第i种物品，那么F[i][j] = F[i-1][j]
如果要取第i种物品， 那么可以先强行往背包里塞一个第i种物品，那么问题转换为：F[i][j] = F[i][j-wi] + vi

F[i][j] = max(F[i-1][j] , F[i][j-wi]+vi )

伪代码

void dp(){
	for (int i = 1; i <= n; i++)
		for (int j = weight[i]; j <= w; j++)
			f[j] = max(f[j], f[j - weight[i]] + value[i]);
}
1
2
3
4
5

四、多重背包问题

在我看来，多重背包问题大概就是在完全背包问题的基础上再进一步思考。

题目：

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci，价值是Wi。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最大。

基本思路

该题特点：每一种物品的数量不同

思路一：完全背包解法

当背包容量为j时，第i种物品的最多可选件数为：
Ki = min(num[i],j/wi)

伪代码

void multiPack(){
   for (int i = 1; i <= n; i++)
	for (int j = w; j >= weight[i]; j--)
		for (int k = 1; k * weight[i] <= j && k <= num[i]; k++)
			f[j] = max(f[j], f[j - k*weight[i]] + k*value[i]);
}
1
2
3
4
5
6

思路二：转换为01背包

但是需要对每件物品的件数ni做分解。
对ni进行二进制拆分，并且拆分的子段和可组成1~ni之间的任意数。
如13 = 1 + 2 + 4 + 6
1,2,4,6 可以组成1~13之间的任意数。
因此可以转换为01背包：
如果要装5个，相当于装入1和4
如果要装7个，相当于装入1、2、4

伪代码

for (int i = 1; i <= n; i++){
	cin >> w_ >> v_ >> num;
	int k = 1;
	while (num >= 0){
		weight[++tot] = k <= num  ?  k*w_  :  num*w_;
		value[tot]  = k <= num  ?  k*v_  :  num*v_;
		num -= k;
		k *= 2;
	}
}
1
2
3
4
5
6
7
8
9
10