-
【LeetCode】215. 数组中的第K个最大元素
题目描述
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4提示:
1 <= k <= nums.length <= 105
-104 <= nums[i] <= 104方法一:优秀解法 – 快排+随机化
class Solution { public: void QuickPartition(vector<int>& nums, int start, int end, int target){ // 随机取一个数 srand(time(nullptr)); int random = rand() % (end - start + 1) + start; int base = nums[random]; // 将这个数放到数组的开头位置 swap(nums[start], nums[random]); int index = start; // 从待排区间的第一个元素开始,依次与随机选择的元素base比较 // 如果大于等于base,就把该元素交换到index+1的位置,index++ // 最终,下标小于index的元素都比base大 for(int i = start+1; i <= end; i++){ if(nums[i] >= base){ swap(nums[i], nums[index+1]); index++; } } // base存放在数组最开始的位置,将其交换到index位置上 // 它前面的元素都比本身大 swap(nums[index], nums[start]); // 如果index恰好等于target,那么就结束函数调用,不会继续迭代 // index比target大,那就在index的左边继续查找 if(index > target) QuickPartition(nums, start, index-1, target); // index比target小,那就在index的右边继续查找 else if(index < target) QuickPartition(nums, index+1, end, target); } int findKthLargest(vector<int>& nums, int k) { // 快排思想+随机化 // 快排是一次找出一个数的正确位置,使得左边的数都比他大, // 右边的数都比他小,返回下标为k-1的值 QuickPartition(nums, 0, nums.size() - 1, k - 1); return nums[k - 1]; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
心得
- 总体思路: 这一题主要就是对数组进行降序排序,返回第k个位置,也就是下标为k-1的元素。常规排序解法时间复杂度都在O(n2),难点在于如何满足O(n2)的时间复杂度。
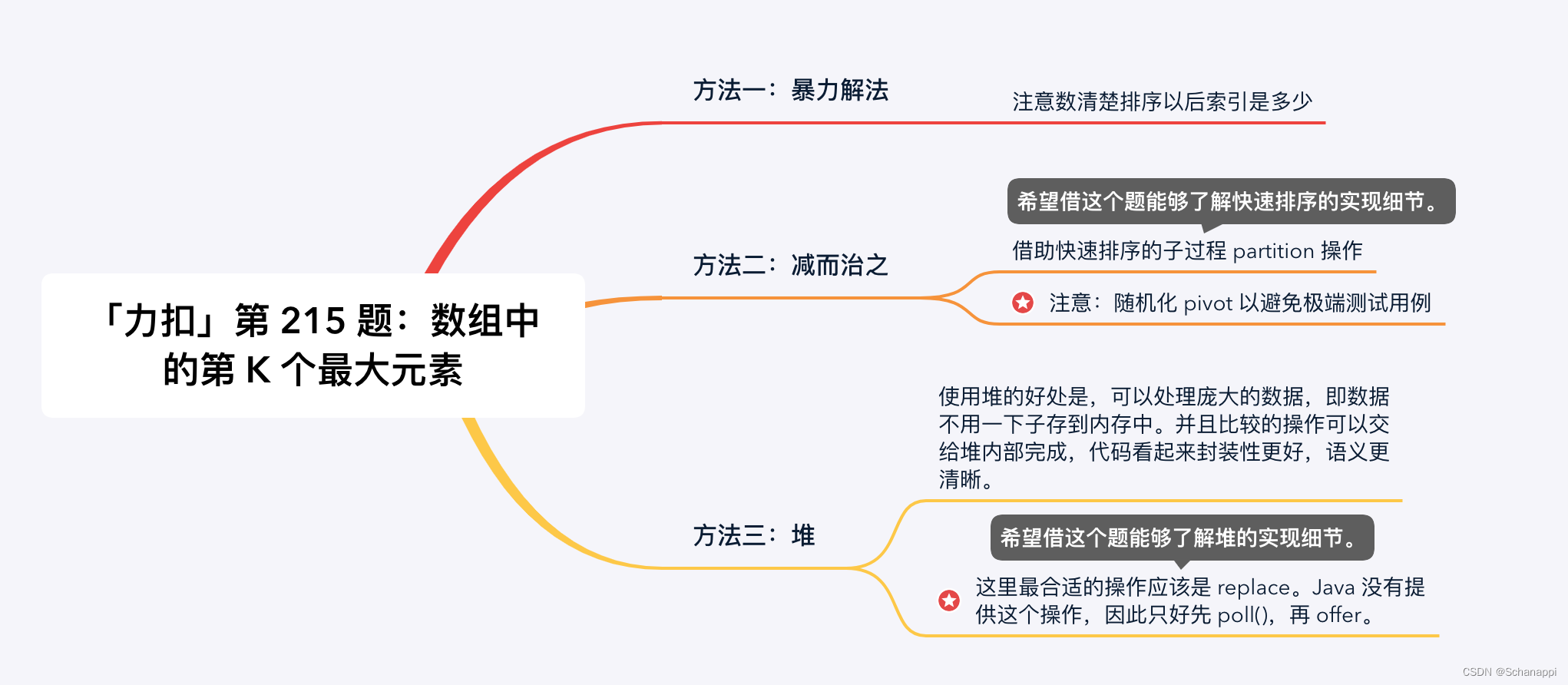
- 解法:快排+随机化
快排的平均时间复杂度为O(n logn),因此需要对快排进行优化。首先,回顾一下快速排序。
1.分解 :将数组arr[left,…,right]划分为两个子数组arr[left,…,q-1]和arr[q+1, …, right],使得第一个子数组的所有元素都小于arr[q],第二个子数组的所有元素都大于arr[q]。
在分解这个步骤,也还有很多方式,除了本文的顺序遍历,还有“填坑法”,放在参考文献。
2.解决:通过递归调用快排,对子数组进行排序。
3.合并:因为子数组都是原址排序,所以不需要进行合并操作,arr[left, …, right]已经有序。
可以发现,在快排操作中,每进行一次划分都可以确定一个元素的最终位置。所以只要某次划分的q下标为k-1时,我们就找到了答案。
因此,我们可以对快排进行优化来解决这个问题,快排性能和划分出的子数组长度密切相关,可以引入随机化来加速快排,它的时间代价的期望为O(n),证明略。 - 这道题还可以用堆排序,涉及大根堆、小根堆,今日所学的知识超标,这个知识点放到以后再学。
参考文献
[1]『 TopK问题 』快速排序、堆排序详解 -
相关阅读:
.Net Nullable reference types(可为空引用类型)
阿里云云效流水线教程
杂牌行车记录仪特殊AVI结构恢复案例
语音增强——谱减法的改进(过减法)及其python实现
WebSocket学习笔记
四、ROS2通信机制(话题)
143、锐捷交换机恢复出厂和各种基本配置
微软 AutoML 框架之 FLAML | 环境配置、安装、分类/回归测试
汽车MCU虚拟化--对中断虚拟化的思考(1)
vue中computed计算属性与methods方法的区别
- 原文地址:https://blog.csdn.net/weixin_43894455/article/details/127790136
