数据结构第三部分——树和二叉树(C语言版)

数据结构第三部分——树和二叉树(C语言版)

一、树

1、树的定义

• 由唯一的根和若干互不相交的子树组成，树的定义是递归的，即每一棵子树又是一棵树。
  

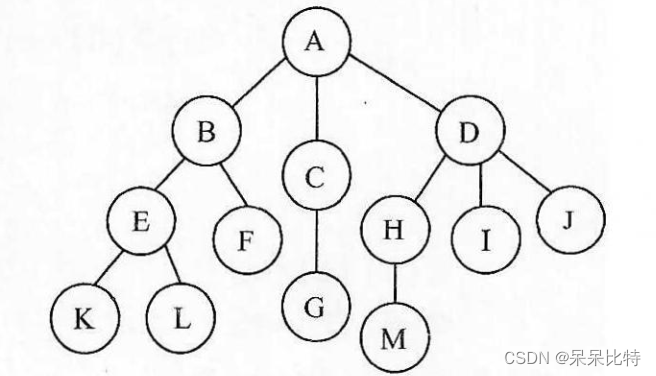
2、树的存储结构

• 顺序存储结构

  • 树的顺序存储结构中最简单的是 双亲存储结构，用一维数组即可实现。
  • 如用一个整型数组存储一棵树：int tree[maxSize];
  • 举一个最简单的例子：
    
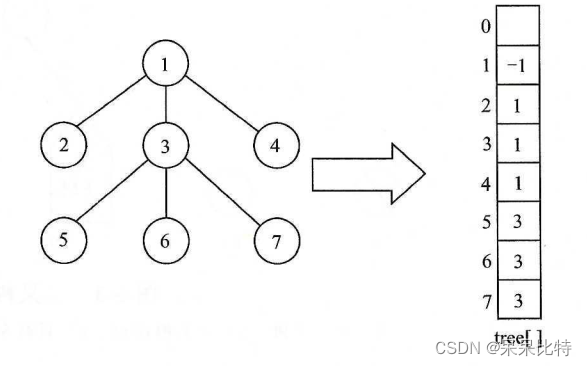
  • 如上图所示，用数组下标表示树中的结点，数组元素的内容表示该结点的双亲结点。
  • 1为根节点，所以数组1索引内容为-1，2,3,4索引内容为1，因为他们的父节点是1…

• 链式存储结构

  • 树的链式存储结构有两种：孩子存储结构 和 孩子兄弟存储结构，孩子存储结构实际上就是图的邻接表存储，树就是一种特殊的图，把图中多对多的关系删减为一对多的关系即得到树。
  • 孩子兄弟存储结构与 树和森林与二叉树的相互转换密切相关，具体在接下来的转换部分。

二、二叉树

1、二叉树的定义

• 给树加上两个限制条件，就得到了二叉树：

  • 1.每个节点最多只有两棵子树，即二叉树中结点的度只能为0、1、2.
  • 2.子树有左右顺序之分，不能颠倒.

• 二叉树的五种基本形态
  

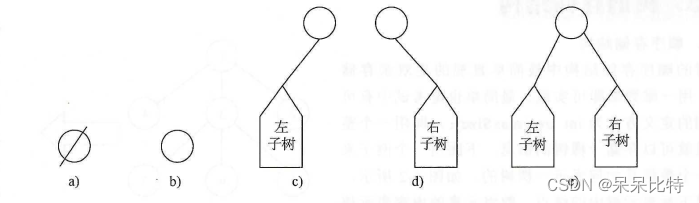
• 如果二叉树所有的分支结点都有左孩子和右孩子结点,并且叶子结点都集中在二叉树的最下一层,则这样的二叉树称为满二叉树（a）；对满二叉树进行编号，约定编号从1开始，从上到下，自左至右进行编号，各结点的编号与满二叉树中相同位置上的结点的编号均相同，那么这棵二叉树就是一棵完全二叉树。
  
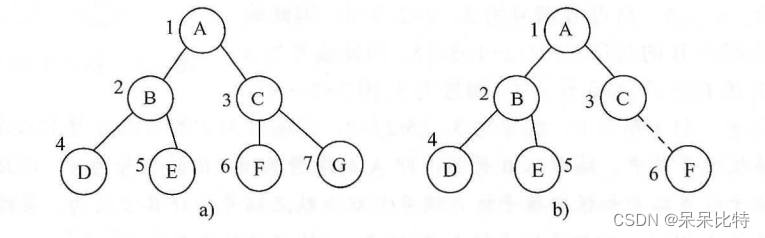
  虚线F不存在即为完全二叉树，否则不是。

2、二叉树的性质

• 普通二叉树
  • 1.非空二叉树上叶子结点数等于双分支结点数加1：n0 = n2 +1
  • 2.二叉树中，第 i 层最多有 2i-1 个结点。
  • 3.如果二叉树的深度为 K，那么此二叉树最多有 2K-1 个结点。
    分隔一行
• 满二叉树除了满足普通二叉树的性质，还具有以下性质
  • 满二叉树中第 i 层的节点数为 2i-1 个。
  • 深度为 k 的满二叉树必有 2k-1 个节点 ，叶子数为 2k-1。
  • 满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。
  • 具有 n 个节点的满二叉树的深度为 log2(n+1)。
    分隔一行
• 完全二叉树除了具有普通二叉树的性质，它自身也具有一些独特的性质
  • n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。
  • 当 i>1 时，父亲结点为结点 [i/2] 。（i=1 时，表示的是根结点，无父亲结点）
  • 如果 2i>n（总结点的个数） ，则结点 i 肯定没有左孩子（为叶子结点）；否则其左孩子是结点 2i 。
  • 如果 2i+1>n ，则结点 i 肯定没有右孩子；否则右孩子是结点 2i+1 。

3、二叉树的存储结构

• 顺序存储结构
  • 顺序存储结构即用一个数组来存储一棵二叉树，将完全二叉树中的结点值按编号依次存入一个一维数组中，即完成了一棵二叉树的顺序存储。
  • 这种存储方式最适合于完全二叉树，用于存储一般二叉树会浪费大量的存储空间。
    分隔一行
• 链式存储结构
  • 所谓二叉树的链式存储，其实就是用链表存储二叉树，具体的存储方案是：从树的根节点开始，将各个节点及其左右孩子使用链表存储。

typedef struct BTNode
{
    DataType data;//数据域
    struct BTNode *lchild;
    struct BTNode *rchild;
}BTNode;
1
2
3
4
5
6

4、二叉树的遍历

• 先序遍历
  • 根 → 左 → 右

void preorder(BTNode *p)
{
	if(p != NULL)
	{
		//对结点操作访问的函数
		Visit(p);
		preorder(p->lchild);
		preorder(p->rchild);
	}
}
1
2
3
4
5
6
7
8
9
10

• 中序遍历
  • 左 → 根 → 右

void inorder(BTNode *p)
{
	if(p != NULL)
	{
		inorder(p->lchild);
		//对结点操作访问的函数
		Visit(p);
		inorder(p->rchild);
	}
}
1
2
3
4
5
6
7
8
9
10

• 后序遍历
  • 左 → 右 → 根

void postorder(BTNode *p)
{
	if(p != NULL)
	{
		postorder(p->lchild);
		postorder(p->rchild);
		//对结点操作访问的函数
		Visit(p);
	}
}
1
2
3
4
5
6
7
8
9
10

• 层序遍历
  • 从左至右，自上而下层层遍历

void level(BTNode *p)
{
	int front,rear;
	BTNode *que[maxSize];//定义一个循环对列，用来记录将要访问层的节点
	front = rear = 0;
	BTNode *q;

	if(p != NULL)
	{
		rear = (rear+1)%maxSize;
		que[rear] = p; //根结点入队
		while(front != rear)
		{
			front = (front+1)%maxSize;
			q = que[front]; //队头结点出队
			Visit(q); //访问队头结点

			if(q->lchild != null)
			{
				rear = (rear+1)%maxSize;
				que[rear] = q->lchild;
			}
			if(q->rchild != null)
			{
				rear = (rear+1)%maxSize;
				que[rear] = q->rchild;
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

5、将树转换为二叉树

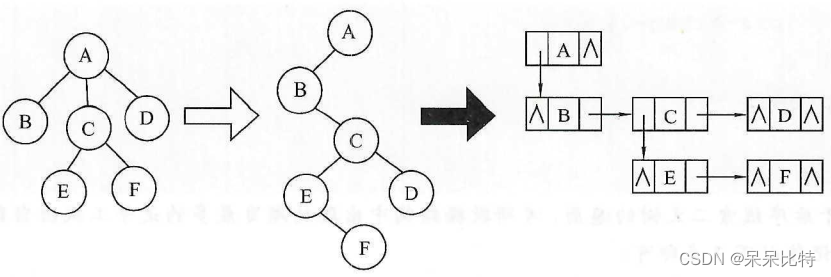
• 1. 将同一结点的各孩子结点用虚线串起来。
• 2. 将每个结点的分支从左往右，除了第一个以外，其余的都剪掉。
     
• 将树转化为二叉树之后，存储在孩子兄弟存储结构中
  

6、将二叉树转换为树

• 1. 先将二叉树进行分层
• 2. 找到每一层结点在其上一层的父结点
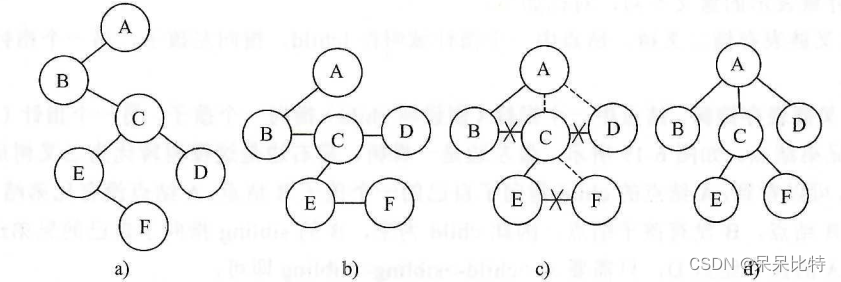
• 3. 连接父结点，删除每一层之间的连接
     

7、赫夫曼树和赫夫曼编码

• 赫夫曼树又叫最优二叉树，他的特点是带权路径最短（带权路径长度：从该结点到根结点之间的路径长度乘以结点的权值）

• 赫夫曼树的构造方法（给定n个权值，用这n个权值来构造赫夫曼树）

  • 将这n个权值分别看作只有根结点的n棵二叉树，这些二叉树构成的集合记为F。
  • 从F中选出两棵根结点的权值最小的树(假设为a、b)作为左、右子树，构造一棵新的二叉树。
  • 新的二叉树的根结点的权值为左、右子树根结点权值之和。
  • 从F中删除a、b，加入新构造的树c。
  • 重复进行上边两步，直到F中只剩下一棵树为止，这棵树就是赫夫曼树。

---