维纳滤波原理极其Python实现

原理

从信号与系统的角度出发，有一部分噪声是系统的固有噪声，另一部分，则是对信号的某种响应，换言之，这部分噪声可以理解为一个噪声系统。所以滤除后者，可以理解为去除噪声系统的影响，换言之，就是针对噪声系统做反卷积。

如果噪声系统可以测量，那么反卷积自然可以顺利执行，否则那就要对这个噪声系统进行估计，维纳滤波履行的就是这个思路。

现有一组观测量 { x i } \{x_i\} {xi​}，由信号和噪声部分组成，即$x_i=y_i+v_i$，$v_i$就是噪声分量。所谓去噪过程，就是找出一组$y_i$的逼近值${\hat{y}}_i$。

所以接下来的问题是，这组量应该怎么找？考虑到求比证难，不妨把这个问题再简化一下，如果找到了一组值，那么如何确定这组值是对的？

正常思路一定是，定义一个误差量$e_i={\hat{y}}_i-y_i$，然后找到这个误差量的某个统计值的极值，考虑到正负号的问题，这个统计量有可能是方差。

而学过信号与系统，就一定会定义一个$h_i$，作为滤波器的冲击响应，则${\hat{y}}_i$可以表示为$h_i$对信号的卷积

$${\hat{y}}_i=\sum _k{h}_k{x}_{i-k}$$

为了便于阅读，可以将上面的式子写为矩阵形式，就是$\hat{y}=hx$，$e=\hat{y}-y$。

接下来就可以用$h$来表示误差量$e$的方差

$$\begin{array}{rl}\epsilon & =E(e^2)=E[(\hat{y}-y{)}^2]\\ & =E[(hx-y{)}^2]\\ & =E[(y^2+hx{x}^T{h}^T-2yhx{)}^2]\end{array}$$

取极值，那就少不了求导，这个$h$就是要求导的量

$$\frac{\partial \epsilon }{\partial h}=E[2x{x}^T{h}^T-2yx]$$

极值点处，偏导数为0，从而得到

$$h=E[(x{x}^T{)}^{-1}]E(xy)$$

有了$h$，相当于有了噪声系统的作用形式，也就可以基于此进行反卷积了。

scipy调用维纳滤波

scipy中封装了维纳滤波，其形式为

scipy.signal.wiener(im, mysize=None, noise=None)
1

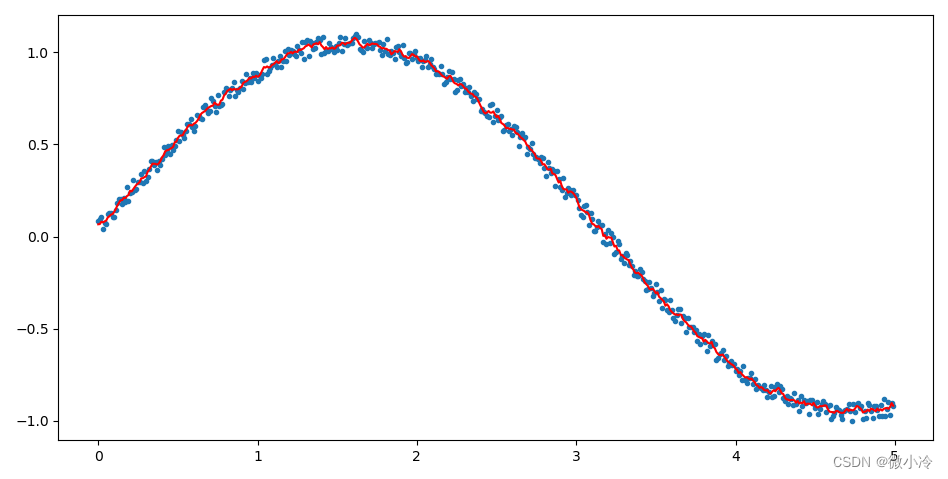
其中，im为待滤波数据，mysize为滤波模板的尺寸，noise为系统的噪声，如果为None，那么将自动估计系统噪声。

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import wiener
x = np.arange(0,5,0.01)
y = np.sin(x)
yhat = y + np.random.rand(len(yhat))*0.1
yFilt = wiener(yhat, 5) # 维纳滤波
plt.scatter(x, yhat, marker='.')
plt.plot(x, yFilt, c='r')
plt.show()
1
2
3
4
5
6
7
8
9
10

效果如下