-
【数据结构初阶】图文详解10道力扣链表OJ题
前言
本文用图文详解得方式给大家讲解链表相关试题,期望大家学到有用的知识
一、移除链表元素

1.1 方法一:尾插法
struct ListNode* removeElements(struct ListNode* head, int val){ if(head==NULL) { return NULL; } struct ListNode*cur=head; struct ListNode*newlist=NULL; struct ListNode*newtail=NULL; while(cur) { if(cur->val==val) { cur=cur->next; } else { if(newlist==NULL) { newlist=newtail=cur; cur=cur->next; } else { newtail->next=cur; newtail=newtail->next; cur=cur->next; } newtail->next=NULL;防止链表形成环!!!! } } return newlist; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32

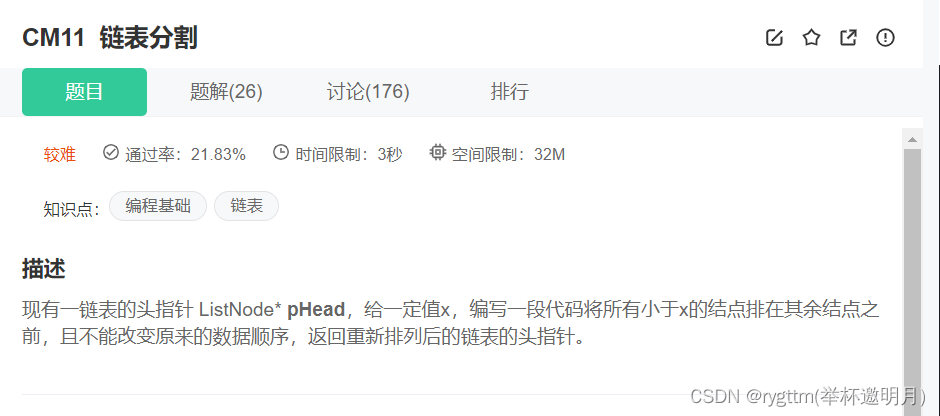
理解误区:
值得注意的是,这里有一个地方很容易造成思维误区,我刚开始理解的时候,我以为我是创造了一个新链表,这个新链表中的结点是没有val值的,但其实这种思维是错误的。
链表中的结点是怎么一个一个链接起来的呢?他其实就是通过记录下一个结点的地址链接起来的,如果我将原链表中想要的结点都拿出来放到一个新的链表上去,自然就得将他们的地址拿出来链接到新的链表上去。
所以尾插法的根本思想其实就是我们改掉了某些结点中next的值,修改了链表中的结点依次连接的顺序,从而产生了一个新的链表,由此也可以想到,原链表也就无法访问到了,因为我们已经将链表进行修改了。
从另一方面来谈:我们是没有malloc新的空间,所以也就不存在创造了一个新的链表这样的事情,归根溯源是我们将链表中的next进行了修改,依次达到了修改链表的目的,有些题目是不允许修改链表的,到时候我们在谈怎么解决那样的问题。1.2 解法二:原地删除法
struct ListNode* removeElements(struct ListNode* head, int val){ if(!head) { return NULL; } struct ListNode*cur=head; struct ListNode*prev=NULL; while(cur) { if(cur->val==val) { if(cur==head) { head=cur->next; free(cur); cur=head; } else { prev->next=cur->next; free(cur); cur=prev->next; } } else { prev=cur; cur=cur->next; } } return head; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
这种方法其实是需要考虑两种不同的结点删除方式的,一种是头删,一种是中间元素的删除。
如果是头删我们需要移动head,如果是中间元素的删除,我们需要利用双指针来解决删除的问题。二、反转链表
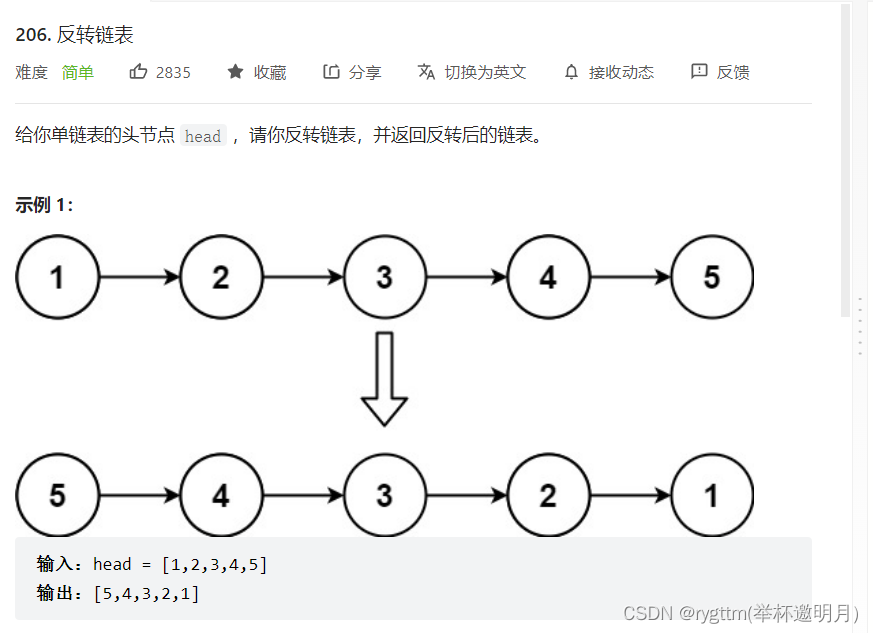
2.1 头插法(cur和next)
struct ListNode* reverseList(struct ListNode* head){ struct ListNode*newlist=NULL; struct ListNode*cur=head; while(cur) { struct ListNode*next=cur->next; cur->next=newlist; newlist=cur; cur=next; } return newlist; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
头插法:头插法就是我们需要不断的重新定义这个头的位置,随着cur指针的遍历,结点的next也被我们改为指向newhead,同时需要不断的将newhead向前移动,所以由于我们改动了此处结点的next,所以我们需要一个指针将下一个结点的地址保存起来。
尾插法:尾插法就不需要保存下一个结点了,因为我们不会讲结点的next改动,我们只是通过cur的遍历,过滤了一些我们不想要的值,然后把想要的结点重新串起来。
三、链表的中间结点
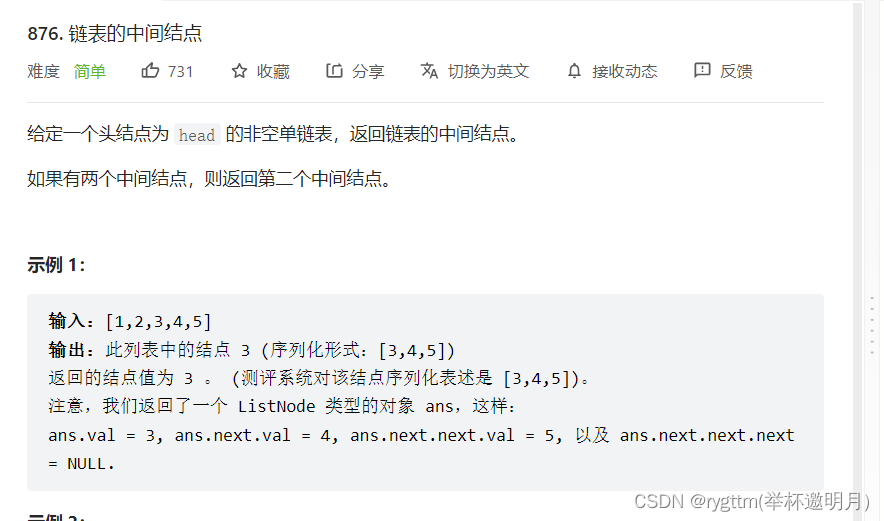
struct ListNode* middleNode(struct ListNode* head){ struct ListNode*slow=head,*fast=head; while(fast&&fast->next) { fast=fast->next->next; slow=slow->next; } return slow; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
四、链表中倒数第k个结点

struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) { // write code here struct ListNode*slow=pListHead,*fast=pListHead; while(k--) { if(!fast) { return NULL; } fast=fast->next; } while(fast) { fast=fast->next; slow=slow->next; } return slow; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
我们可以让快指针先走K步,然后两个指针同时去走,当快指针走到NULL时,两者一起走的步数停止,此时我们慢指针slow所在的位置就是链表中倒数第K个结点的位置。
怎么想到这样的方法呢?其实很简单,我们讲链表倒过来看以NULL所在位置的索引记为0那么,从NULL开始往前数k步,那么其实就是我们的倒数第k个结点,所以我只要控制快慢指针的距离差为k当快指针走到我们的索引为0,也就是NULL位置的时候,slow和fast之间正好差了k个距离差的单位,此时slow恰好在倒数第k个结点的位置上。
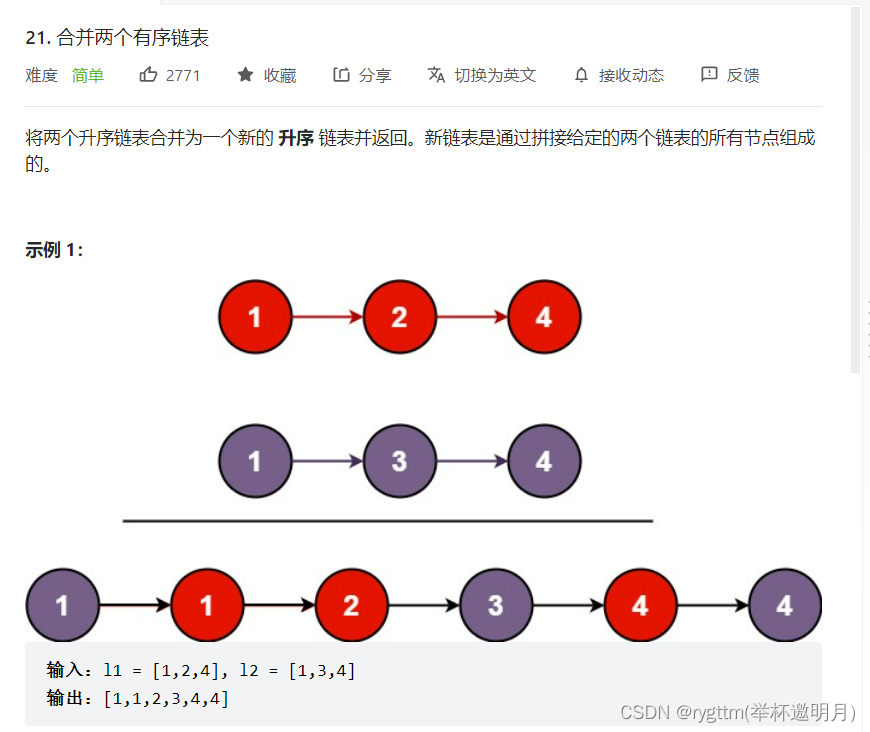
五、合并两个有序链表
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) { if(list1==NULL) { return list2; } if(list2==NULL) { return list1; } struct ListNode*newlist=NULL,*newtail=NULL; struct ListNode*cur1=list1,*cur2=list2; while(cur1&&cur2) { if(cur1->val>cur2->val) { if(newlist==NULL) { newlist=newtail=cur2; } else { newtail->next=cur2; newtail=cur2; } cur2=cur2->next; } else { if(newlist==NULL) { newlist=newtail=cur1; } else { newtail->next=cur1; newtail=cur1; } cur1=cur1->next; } } if(cur1==NULL) { newtail->next=cur2; } else { newtail->next=cur1; } return newlist; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
这个合并两个有序链表的题,思路还是比较简单的,我们主体思路还是进行我们的尾插,依次比较两个链表中的每个结点,将value值较小的那个结点尾插到我们的newlist上面,当遍历结束之后,一定有一个链表是没有遍历完的,所以我们还需要在while循环的外面重新判断一下哪个链表已经遍历结束了,将未遍历结束的链表直接尾插到我们的newtail指针的后面。
不过这个题其实还有另外一种做法,因为每次刚开始尾插的时候,我们还得先将第一个较小的结点的地址赋值给我们的newlist,如果想要避免这样的操作,我们可以使用带有哨兵卫的头结点来处理这样的问题,可以省下赋值的那一步操作,我们来看一下带有哨兵卫的头节点该怎么操作吧!
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) { if (list1 == NULL) { return list2; } if (list2 == NULL) { return list1; } struct ListNode*newlist=(struct ListNode*)malloc(sizeof(struct ListNode)); newlist->next=NULL; struct ListNode*newtail=newlist; while(list1&&list2) { if(list1->val>list2->val) { //我们可以省下判断,直接进行尾插了 newtail->next=list2; newtail=list2; list2=list2->next; } else { newtail->next=list1; newtail=list1; list1=list1->next; } } if(list1==NULL) { newtail->next=list2; } else { newtail->next=list1; } struct ListNode*newhead=newlist->next; free(newlist); return newhead; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
当我们向堆区申请空间一块儿带有哨兵卫头结点后,我们在第一次尾插时就不需要进行那个赋值操作了,因为我们的修改链表他已经有头结点了,所以我们只需要将较小结点尾插到这个修改链表之后就可以了。
值得注意的是,在程序结束的时候,我们要将申请的空间free掉将其还给操作系统
六、链表分割
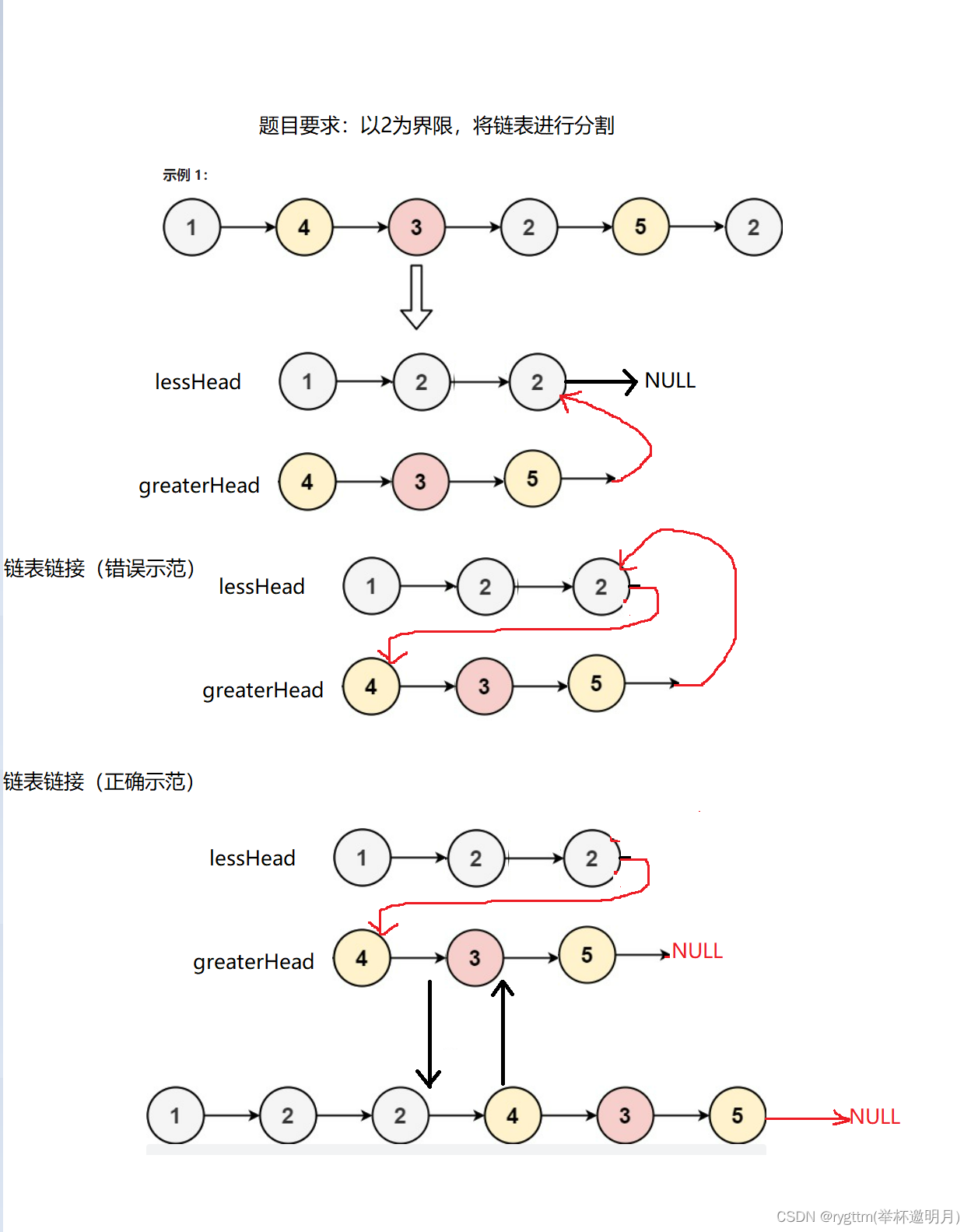
思路:如果在链表原地进行修改,代码实现起来其实是比较困难的,所以我们不对链表进行原地修改,我们将链表中的结点拿出来,重新放到两个修改后的链表,一个链表放小于x的所有结点,一个放大于等于x的所有结点,最后我们在将这两个链表链接起来,这样我们的链表分割就完成了
当然,这里面其实又隐含了我们之前的一种想法,其实就是尾插,因为我们的尾插不会改变next,可以很好保留原来链表中结点的相对顺序,既然是尾插,我们又遇到了一个子问题,这个子问题其实就是,刚开始尾插时,我们不能进行尾插,需要将指针我们的链表中第一个较小结点的地址赋值,为了避免这样的冗余操作,我们直接就使用带有哨兵卫的头结点的方式来解决这样的问题。class Partition { public: ListNode* partition(ListNode* pHead, int x) { // write code here struct ListNode*greaterHead=NULL,*greaterTail=NULL,*lessHead=NULL,*lessTail=NULL; greaterTail=greaterHead=(struct ListNode*)malloc(sizeof(struct ListNode)); greaterTail->next=NULL; lessHead=lessTail=(struct ListNode*)malloc(sizeof(struct ListNode)); greaterTail->next=NULL; struct ListNode*cur=pHead; while(cur) { if(cur->val<x) { //我们将他尾插到lessHead lessTail->next=cur; lessTail=cur; cur=cur->next; } else { //我们将他尾插到greaterHead greaterTail->next=cur; greaterTail=cur; cur=cur->next; } } greaterTail->next=NULL;//防止形成环 //现在将两个链表链接起来 lessTail->next=greaterHead->next; struct ListNode*trueHead=lessHead->next; free(lessHead); free(greaterHead); return trueHead; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
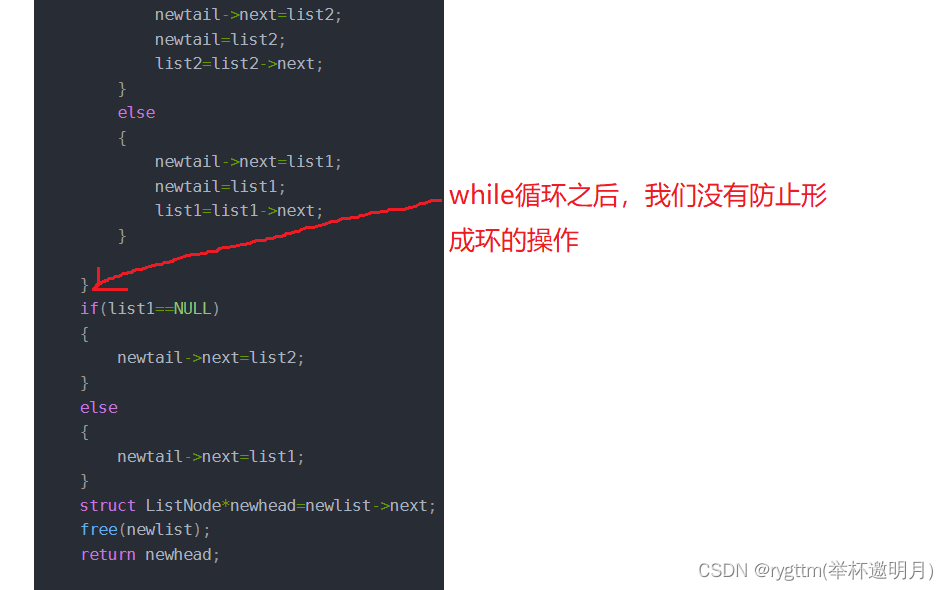
值得注意的是,我们这里遍历完原链表之后,大家想必也看到了greaterTail->next=NULL; 这样的一句代码,这个代码其实是防止我们分割之后的链表形成环的,如果形成环的话,其实是会造成死循环的。
这里其实还是要与我们的链表合并对比一下的,我们可以看到,我们不用将某一个链表尾部置空的操作,这是为什么呢?因为我们的两个链表中的任何一个链表的尾结点肯定有一个做的是新链表的尾结点,所以我们的新链表尾部的next一定是指向空的,所以我们是不用自己操作防止形成环的。
而分割链表其实是不一样的,因为修改之后的新链表的尾结点它不一定是我们原链表的尾结点,所以我们是需要自己greaterTail->next=NULL; 置空的,以防止我们的链表形成环。
七、链表的回文结构
7.1 博主踩过的大坑(吐槽牛客)
当时我做这个题,可是被牛客网坑惨了,因为他的测试用例过少,导致我写了一个错误的代码牛客系统还给我通过了,然后我一度认为我自己的思路和代码是正确的,但当时脑子里产生了一个我现在忘掉了的问题,我向大佬请教过后,才发现,我有很多理解上的错误,这一下就将我有错误的地方一条链扯出来了,说了这么多废话,好家伙,进入正题。
当时我想的是,这不是链表回文嘛,我只要拥有这个链表逆置过后的链表,然后拿逆置的链表与原链表一个一个结点进行比较,如果不相等那么这个链表就不是回文结构,而且,具体实现的话也简单,我们前面利用头插法是进行过的逆置的,所以逆置目前这个链表问题也是不大的,可惜理想很丰满,显示很骨感。
我们这样的想法完全错误,错误的彻彻底底!为什么呢?其实在文章开头部分,我也做了铺垫了。原因就是,我们的原链表已经被我们修改了,所以压根不存在拿逆置的与原来的进行比较这一说。
因为我们逆置的本质其实就是修改链表,将原来链表进行修改。
所以正确的思路应该是,我们找到链表中间的部分,将链表分为两个链表,然后再将后半部分链表进行逆置,最后我们分别从两个链表的头结点开始进行比较,比到最后如果都相等,也就说明了这个链表是回文结构的。
回文链表=寻找中间结点+逆置链表

class PalindromeList { public: bool chkPalindrome(ListNode* A) { // write code here //1.找到中间结点 //2.后半部分逆置 //3.向中间结点遍历 struct ListNode*slow=A,*fast=A; while(fast&&fast->next) { fast=fast->next->next; slow=slow->next; } struct ListNode*headB=NULL; struct ListNode*cur=slow; while(cur) { struct ListNode*next=cur->next; cur->next=headB; headB=cur; cur=next; } while(A&&headB) { if(A->val!=headB->val) { return false; } A=A->next; headB=headB->next; } return true; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
八、"香蕉"链表

8.1 暴力求解
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) { struct ListNode *cur1=headA,*cur2=headB; for(;cur1;cur1=cur1->next) { cur2=headB;//不要忘记将cur2重置,因为每次内层for循环结束之后,我们的cur2都会到NULL的位置 for(;cur2;cur2=cur2->next) { if(cur1==cur2) { return cur1; } } } return NULL; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
这里实现的思路应该是比较简单的,就是依次拿第一个链表中的结点和第二个链表中的每一个结点进行比较,如果相等则返回相等结点的地址就可以了。但唯一的缺陷就是时间复杂度是O(N²)。如果题目要求时间复杂度是O(N)的话,这样的方法显然就不可行了。
8.2 链表长度差
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) { struct ListNode *tailA=headA,*tailB=headB; int i1=0,i2=0; while(tailA) { tailA=tailA->next; i1++; } while(tailB) { tailB=tailB->next; i2++; } int gab=abs(i1-i2); struct ListNode *longlist=headA; struct ListNode *shortlist=headB; if(i1<i2) { longlist=headB; shortlist=headA; } while(gab--) { longlist=longlist->next; } while(longlist) { if(longlist==shortlist) { return longlist; } longlist=longlist->next; shortlist=shortlist->next; } return NULL; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
要求时间复杂度不能是O(N²),我们就不可以对链表进行循环嵌套这种方式的访问,但我们可以对链表进行多次的循环遍历。
所以我们的思路就是,如果现在有两个相同的链表,我们想要求他们的第一个相交结点的话,那简直太简单了,我们只需要同时遍历两个链表,如果在遍历过程中出现结点地址相等的情况,我们直接返回就好了。所以我们现在其实是想让两个链表一起走,那么我们只要先让那个较长的链表走链表长度差的步数就好了,然后让两个链表在同时一起走,这样就可以完美解决我们的问题了。
九、环形链表|
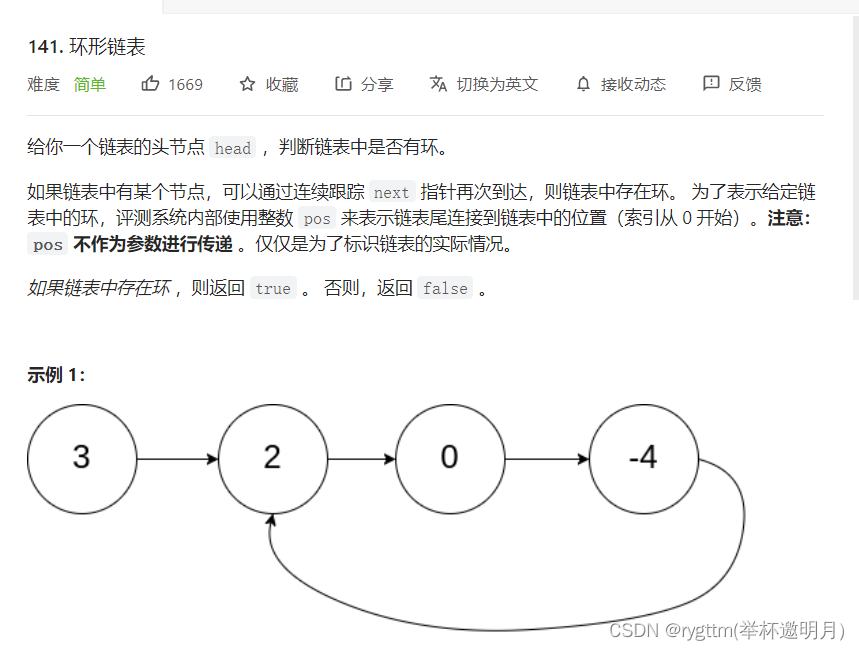
9.1 快慢指针法
这个题我们采用的思想依旧还是快慢指针,我们让快指针一次走两步,慢指针一次走一步,如果链表中有环的话,slow和fast一定会在环中相遇的。
下面我们来给大家稍微证一下,为什么会是这个样子。
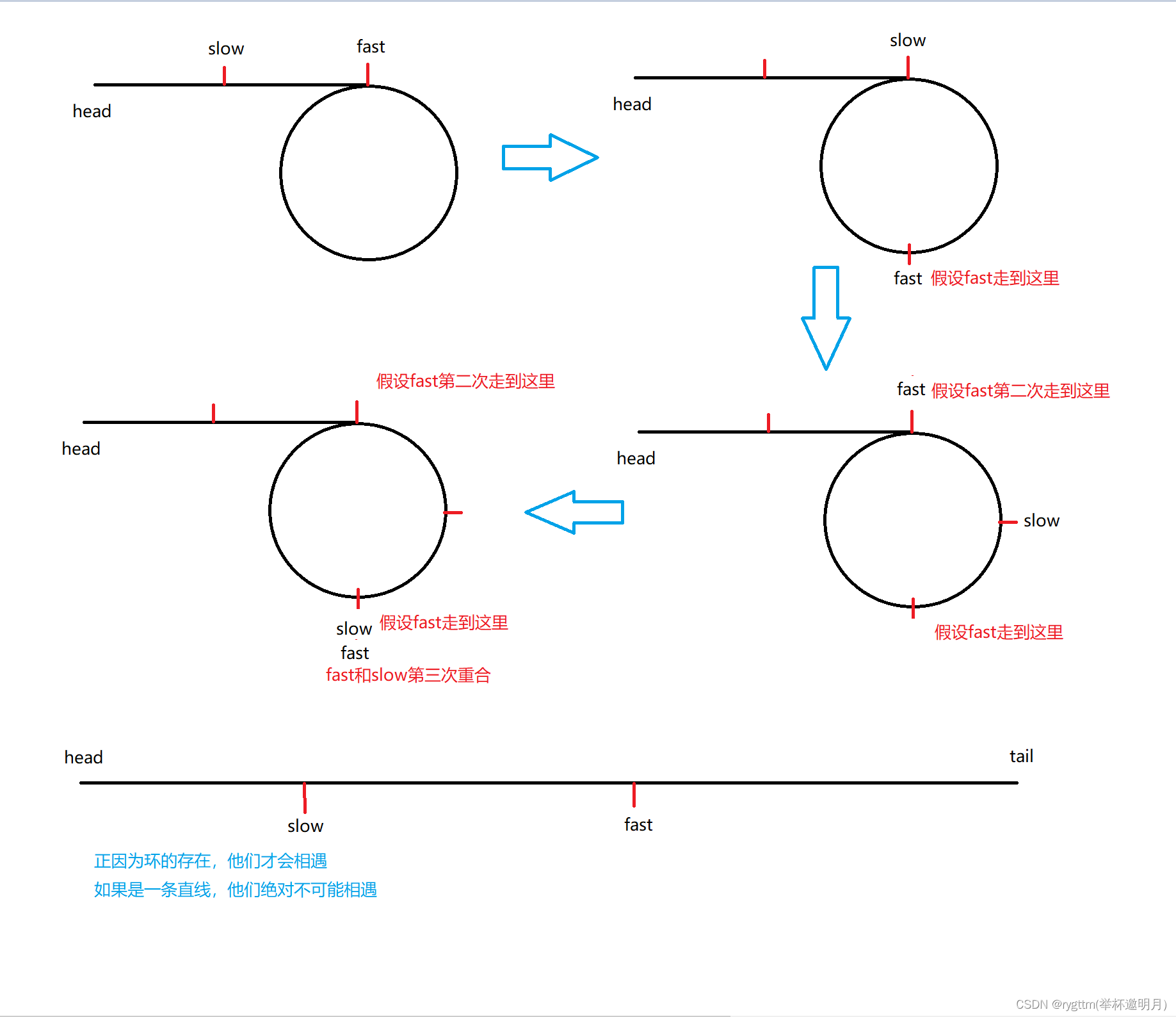
其实道理很简单,如果你被一只野兽在环形笼子里面追,野兽每次走两步,你每次走一步,那无论你和野兽刚开始距离有个几万米还是几亿米,都没有用,你最终一定会被野兽吃掉的,因为他的步数比你多1,你们之间的距离每一次都会-1,最终一定会相遇的bool hasCycle(struct ListNode *head) { struct ListNode *slow=head,*fast=head; while(fast&&fast->next)//一个结点和空链表的情况也可以解决 { fast=fast->next->next; slow=slow->next; if(slow==fast) { return fast; } } return false; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
我们这里在简单介绍一下代码实现的一些细节,我们将循环条件控制为寻找链表中间结点拿到题的控制条件,这样可以很好的帮我们过滤掉链表为单链表的情况还有空链表的情况,这时我们只要直接返回false就可以了,因为这个链表尾结点指向的是NULL,所以他一定不可能带有环。
9.2 延伸问题
1.为什么slow和fast一定会在环中相遇?会不会在环里面错过,永远遇不上?请证明一下。
这个证明其实是比较简单的,fast一定先比slow进环,在这样的先决条件下,我们就可以下结论了,当slow进环时,我们假设此时slow和fast之间的距离是N(N=0,1,2,3,4……),由于fast比slow快一步,那么我们的距离是按照1的单位逐渐减小的,所以我们的距离变化是N,N-1,N-2,N-3……直至减到0,则slow和fast一定会相遇不会错过。
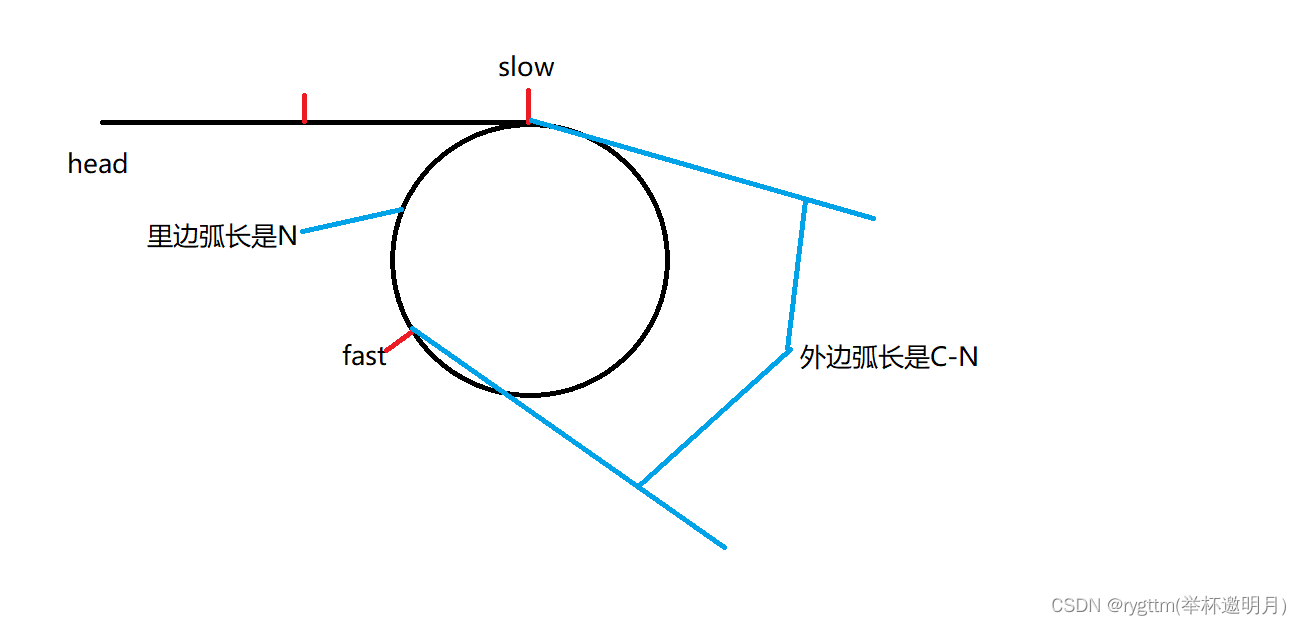
2.为什么slow走一步,fast走两步呢?能不能fast一次走n步呢?
如果fast一次走2步的话,那我们的距离变化就是N,N-2,N-4,N-6,这时能否减到0,就取决于我们的N的大小了,如果N是奇数则这一次无法相遇,我们需要考虑,fast在C-1的距离里面能否再次遇到slow,这又取决于我们的环的大小,但N若为偶数的话,第一次就可以相遇了。
所以通过fast走三步的例子我们就可以看出,能否追上是由许多其他因素控制的,自然当fast走n步的时候,也就不一定能相遇了,所以为了保证fast一定追上slow,我们就得保证fast一次走两步,让他们的距离一次-1,直到距离变为0.十、环形链表||
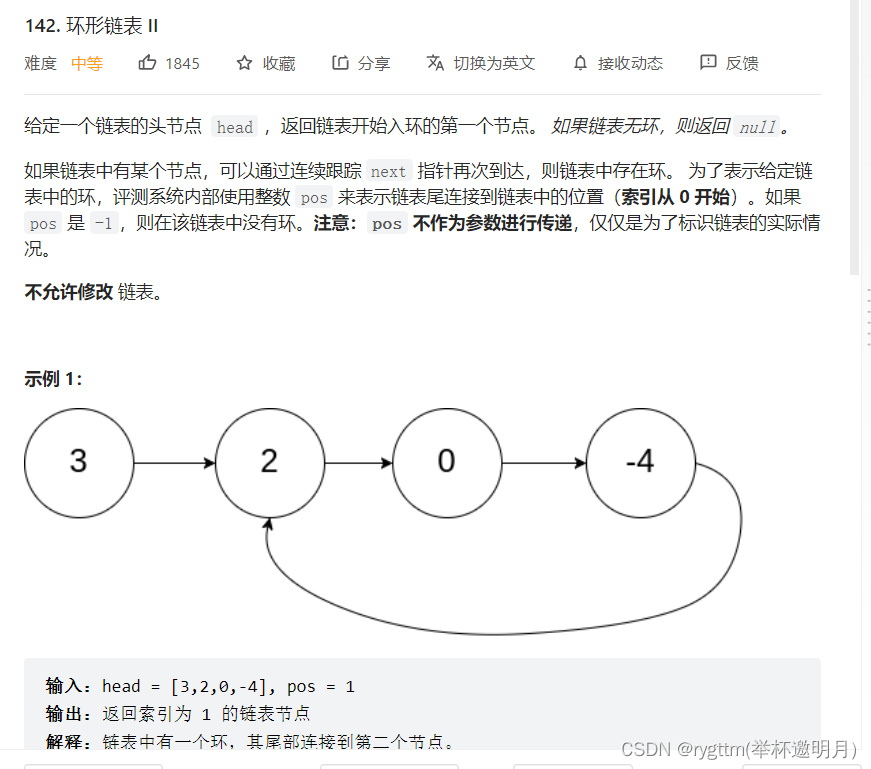
10.1 快慢指针
我们先用图的方式来给大家证明,然后着重在文字介绍一下一些细微的证明点!
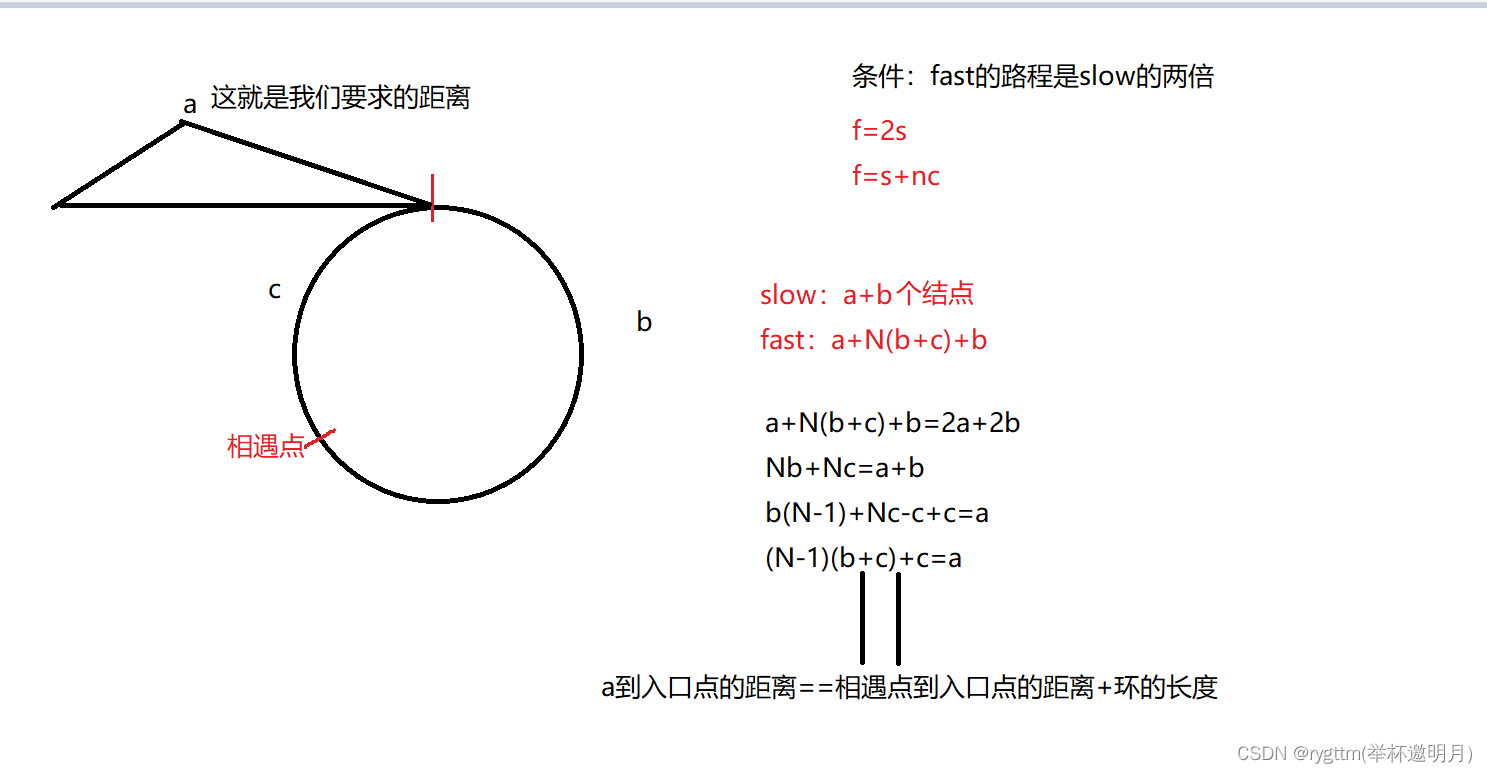
疑问1: 为什么fast走的距离中含有N倍的环的长度呢?fast不转圈,可以追上slow吗?
我们的fast要想追到slow,他是一定要转圈的,至于转圈的个数这取决于环的大小,我们可以反证一下,假设我们的fast一圈都不转就和我们的slow相遇了,那是不是就说明fast没有环就追上slow了呀,可惜了,没有环怎么可能两指针相遇呢?这与我们最基本的想法都背道而驰了,显然这样的说法是错的。那么就可以说明,我们的fast一定是转了几圈之后,才和slow相遇了。
疑问2: 为什么slow只走b的距离呢?slow为什么不可以走圈的距离啊?
因为我们的fast距离是slow的两倍,在slow转一圈的时候,我们的fast都转两圈了,这也就意味着,我们的fast已经比slow多走一圈了,那必然追上两次了都,所以slow没有走一圈的时候,我们的fast就已经追上slow了。struct ListNode *detectCycle(struct ListNode *head) { struct ListNode *slow=head,*fast=head; while(fast&&fast->next) { fast=fast->next->next; slow=slow->next; if(slow==fast)//他们一定是会相遇的,如果有环 { struct ListNode *headTwice=head; struct ListNode *meetnode=slow; while(meetnode!=headTwice) { meetnode=meetnode->next; headTwice=headTwice->next; } return meetnode; } } return NULL; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
10.2 转换成链表相交的问题
这个代码实现起来比较麻烦,思路倒是比较简单,至于代码的实现就交给你们了,我说说思路就好了。
思路还是比较简单的,我们利用快慢指针的方法将meetnode找出来,然后将这个meetnode作为标志点,将meetnode的下一个结点作为另一条链表的头节点,将我们的求环入口结点的问题,转换成两条链表相交的问题。
继续遍历两条链表,让较长链表先走gab步,然后两个链表一起走,第一个相遇的结点就是我们的环入口结点

-
相关阅读:
数据库连接池种类、C3P0数据库连接池、德鲁伊数据库连接池
网络安全:windows批处理写病毒的一些基本命令.
PHP包含读文件写文件
前端加密和解密
SOLIDWORKS二次开发——拓展设计能力与定制化解决方案
CF-957(D-E)
制造业生产运营管理系统如何定义?这些你做到了吗
python实现.jpeg转.jpg
算法&数据结构 - 栈相关基础概念
Pandas中的宝藏函数-map
- 原文地址:https://blog.csdn.net/erridjsis/article/details/127719870
