每日一题：【LeetCode】764. 最大加号标志

题目

在一个 n x n 的矩阵 grid 中，除了在数组 mines 中给出的元素为 0，其他每个元素都为1。mines[i] = [xi,yi]表示 grid[xi][yi] == 0

返回 grid 中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志，则返回 0 。

一个 k 阶由 1 组成的 “轴对称”加号标志具有中心网格 grid[r][c] == 1，以及4个从中心向上、向下、向左、向右延伸，长度为 k-1，由1组成的臂。注意，只有加号标志的所有网格要求为1，别的网格可能为 0 也可能为1 。

示例 1：

输入: n = 5, mines = [[4, 2]]
输出: 2
解释: 在上面的网格中，最大加号标志的阶只能是2。一个标志已在图中标出。

示例 2：

输入: n = 1, mines = [[0, 0]]
输出: 0
解释: 没有加号标志，返回 0 。

提示：

1 <= n <= 500
1 <= mines.length <= 5000
0 <= xi, yi < n
每一对 (xi, yi) 都不重复

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/largest-plus-sign
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

法1：遍历，判断每一个位置上可形成的k阶加号
很不幸超出时间限制了

class Solution:
    def orderOfLargestPlusSign(self, n: int, mines: List[List[int]]) -> int:
        k=0
        grid=[[1 for i in range(n)] for j in range(n)]
        for i in mines:
            grid[i[0]][i[1]]=0
        for i in range(n):
            for j in range(n):
                if grid[i][j]==0:
                    continue
                ki=1
                l=1
                while i-l>=0 and i+l<n and j-l>=0 and j+l<n:
                    if grid[i-l][j]==0 or grid[i+l][j]==0 or grid[i][j-l]==0 or grid[i][j+l]==0:
                        break
                    ki+=1
                    l+=1
                if ki>k:
                    k=ki
        return k
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

法2：官方的动态规划
说实话我一开始瞅那代码大半天硬是没搞懂它在干什么
看不懂就自己举个例子跟着它的代码一步一步推（个人认为这个方法对我比较有效，我写代码理不清思路的很多时候都会举个例子然后推一遍）
下面放了一个4阶矩阵，（3,2）为0的例子，推了上面i的循环，你们可以自己动手全部推一遍
上图

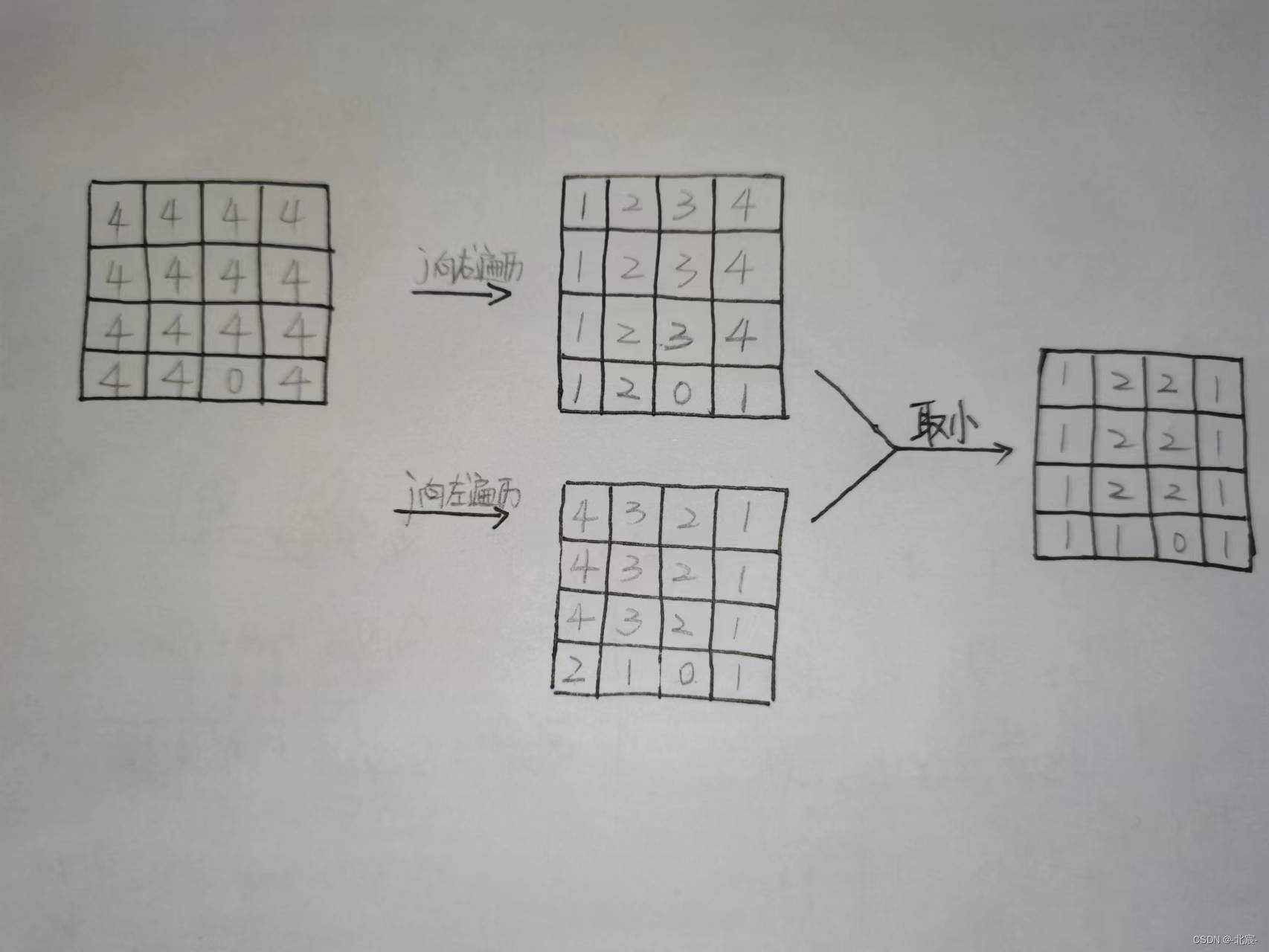
首先将n阶矩阵的所有数赋值为n（因为最大的k阶加号，k一定小于n）
i 循环里的第一个j循环是向右遍历的但是求的是当前位置的左边有几个连续的1（包含当前位置），遇到0时，重新开始计数，将当前位置的计数与原数取小，这样就得到了第一个图
第二个j循环向左遍历，求当前位置的右边有几个连续的1（包含当前位置），得第二个图
将两个图逐位取小，得第三个图，即当前位置左右连续1的最小个数（这一步在第二个j循环时已经同步完成，为方便理解，我另外写出）
同理，j循环下的两遍i循环结束后，得到的结果是当前位置四边连续1的最小个数，即加号的阶数
遍历整个矩阵，所得最大数即为最大加号阶数

class Solution:
    def orderOfLargestPlusSign(self, n: int, mines: List[List[int]]) -> int:
        k=0
        grid=[[n for i in range(n)] for j in range(n)]
        for i in mines:
            grid[i[0]][i[1]]=0
        for i in range(n):
            count=0
            for j in range(n):
                count+=1
                if grid[i][j]==0:
                    count=0
                grid[i][j]=min(grid[i][j],count)
            count=0
            for j in range(n-1,-1,-1):
                count+=1
                if grid[i][j]==0:
                    count=0
                grid[i][j]=min(grid[i][j],count)
        for j in range(n):
            count=0
            for i in range(n):
                count+=1
                if grid[i][j]==0:
                    count=0
                grid[i][j]=min(grid[i][j],count)
            count=0
            for i in range(n-1,-1,-1):
                count+=1
                if grid[i][j]==0:
                    count=0
                grid[i][j]=min(grid[i][j],count)
        return max(map(max, grid))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33