【笔试题】【day20】

目录

第一题（循环队列的数据元素个数的计算）

第二题（二叉树的度）

第三题（平衡因子为0的分支节点，平衡树的构建）

第四题（堆的构建）

第五题（散列冲突） 

第六题（快速排序的结果问题） 

---

第一题（循环队列的数据元素个数的计算）

现有一循环队列，其队头指针为front，队尾指针为rear；循环队列长度为N。其队内有效长度为（）(假设队头不存放数据)

A (rear - front + N) % N + 1
B (rear - front + N) % N
C (rear - front) % (N + 1)
D (rear - front + N) % (N - 1)

	rear					front
2	3						1
0	1	2	3	4	5	6	7

上面的图例中，我们的第一行是我们的f和r的指向

第二行是我们存储的数据1,2,3

最后一行是我们的编号

然后我们的rear-front就需要加上N，然后再取模N，也就是（1-6+8）%8=3

也就是得到了我们的队列的数据元素个数

B

第二题（二叉树的度）

下述结论中,正确的是()

①只有一个结点的二叉树的度为0;

②二叉树的度为2;

③二叉树的左右子树可任意交换;

④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树

A ①②③
B ②③④
C ②④
D ①④

①二叉树的度是二叉树的所有结点中分支最多的那一个，只有一个结点，没有左右分支，所以度为0

②二叉树的度不一定为2，因为二叉树比方说只有单侧有数，那么度就是1，如果是空树，度为0，可以是0,1,2

③二叉树是一棵有序树，如果二叉树的左右的子树没有按照正确的左右顺序去摆放，我们的二叉树跟我们的原来的二叉树并不是同一棵二叉树

④完全二叉树比满二叉树，就是在最后一层的叶子结点从右往左可以缺失部分的结点。满二叉树是一种特殊的完全二叉树。所以是正确的。

D

第三题（平衡因子为0的分支节点，平衡树的构建）

若将关键字1，2，3，4，5，6，7 依次插入到初始为空的平衡二叉树 T 中，则 T 中平衡因子为 0 的分支结点的个数是（ ） 

A 0
B 1
C 2
D 3

首先插入1,2两个结点

 

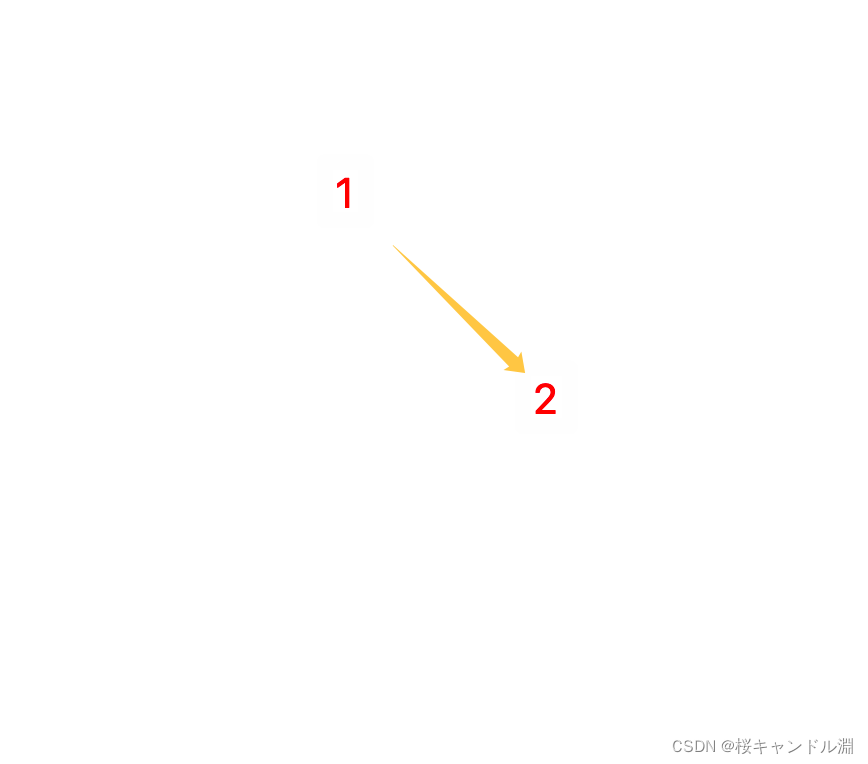
插入3结点时发生左旋 

 

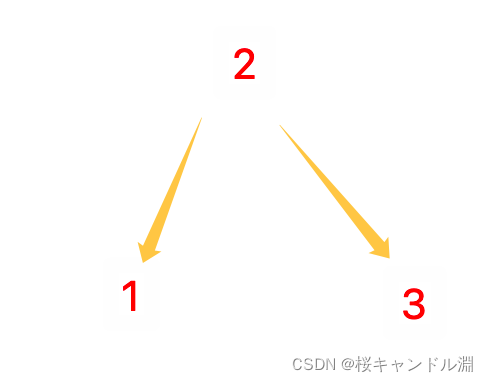
插入4结点，还是平衡的 

 

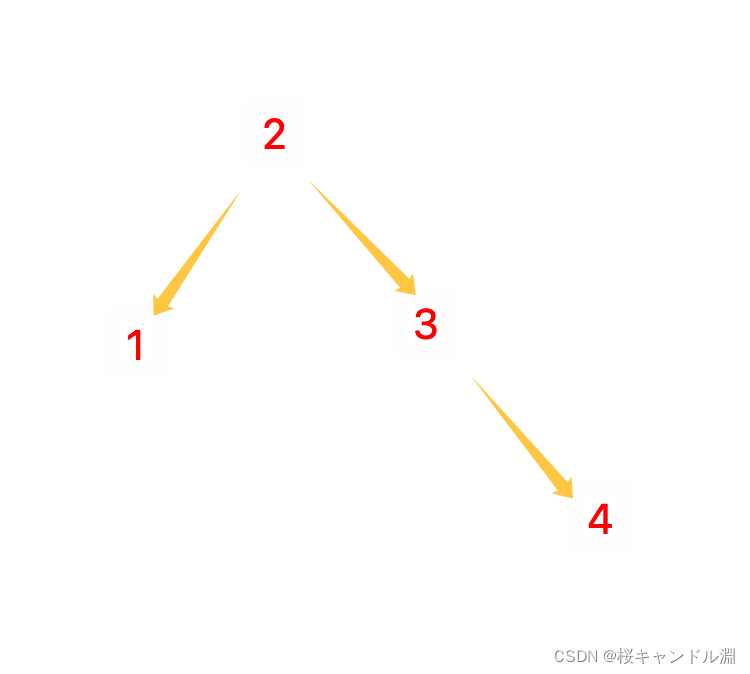
 插入5结点，发生左旋

 

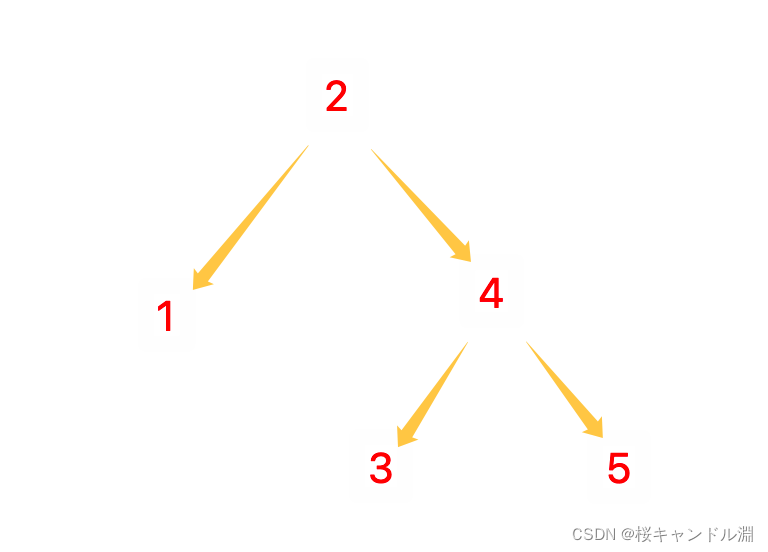
 插入6时发生左右旋

 

 插入7时发生左旋

 

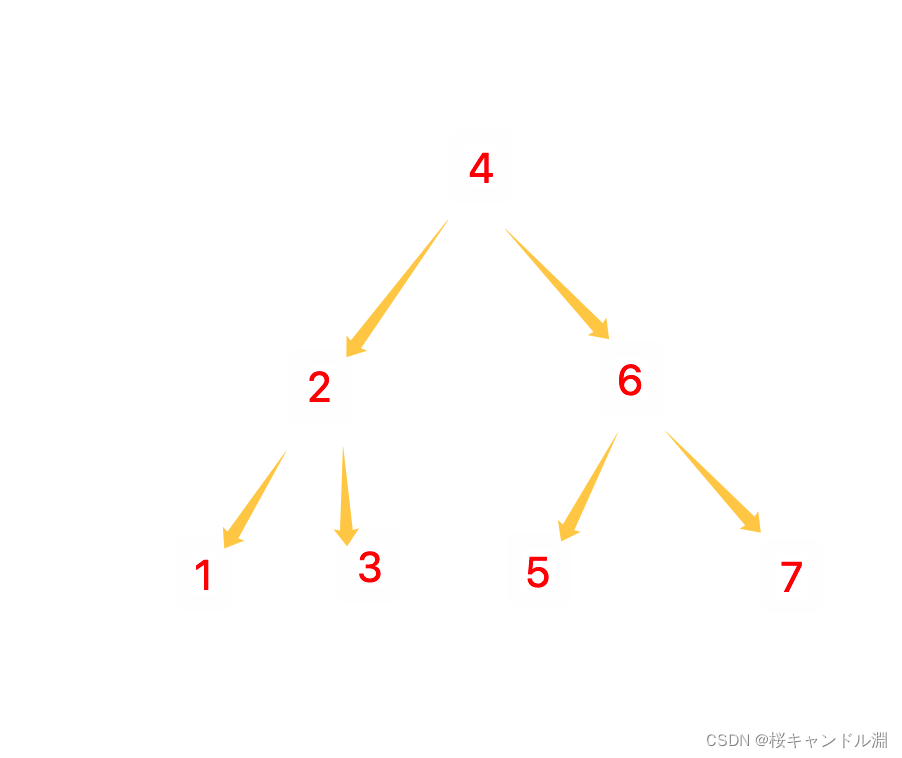
 因为题目问的是分支节点的平衡因子为0的结点，所以我们不能将叶子结点计入其中，所以只有我们的2,4,6结点满足了条件，也就是一共有三个。

D

第四题（堆的构建）

初始序列为1 8 6 2 5 4 7 3一组数采用堆排序，当建堆（小根堆）完毕时，堆所对应的二叉树中序遍历序列为（）

A 8 3 2 5 1 6 4 7
B 3 2 8 5 1 4 6 7
C 3 8 2 5 1 6 7 4
D 8 2 3 5 1 4 7 6

初始序列

                          1

               8                 6

        2        5         4         7

3

                          1

               8                 4

        2        5         6        7

3

 

                          1

               2                 4

        8        5         6         7

3

                          1

               2                 4

        3        5         6         7

8

 

调节完毕 

中序遍历一下为83251647，也就是我们的A

A

第五题（散列冲突） 

解决散列法中出现冲突问题常采用的方法是（）

A 数字分析法、除余法、平方取中法
B 数字分析法、除余法、线性探测法
C 数字分析法、线性探测法、多重散列法
D 线性探测法、多重散列法、链地址法

数字分析法不经常使用

除留余数法仅仅是解决哈希映射的问题，并不能解决冲突

解决冲突只能是 线性探测法、多重散列法、链地址法

D

第六题（快速排序的结果问题） 

下列选项中，不可能是快速排序第2趟排序结果的是 （）

A 2,3,5,4,6,7,9
B 2,7,5,6,4,3,9
C 3,2,5,4,7,6,9
D 4,2,3,5,7,6,9

快速排序是先找到一个关键值，然后关键值左边的元素全部都小于这个关键值，右边的元素全部都大于这个关键值。

然后我们的再递归这个关键值的左右两边，从而将我们的数据全部都排成序列

也就是说每一次排序都有一个以上的数字找到了它应该在的位置

而C 

3,2,5,4,7,6,9

排序的结果应该是

2,3,4,5,6,7,9

只有9找到了它的位置，不可能是我们快速排序的结果。

C