-
论文阅读笔记《Deep Learning of Graph Matching》
核心思想
本文首次提出一种基于深度学习的图匹配方法(GMN),提出了从特征提取,仿射矩阵构建,幂迭代,双随机矩阵生成,投票法到损失计算的完整可微分的图匹配流程,并给出了相应的反向传播的导数计算方法。方法的流程如下图所示
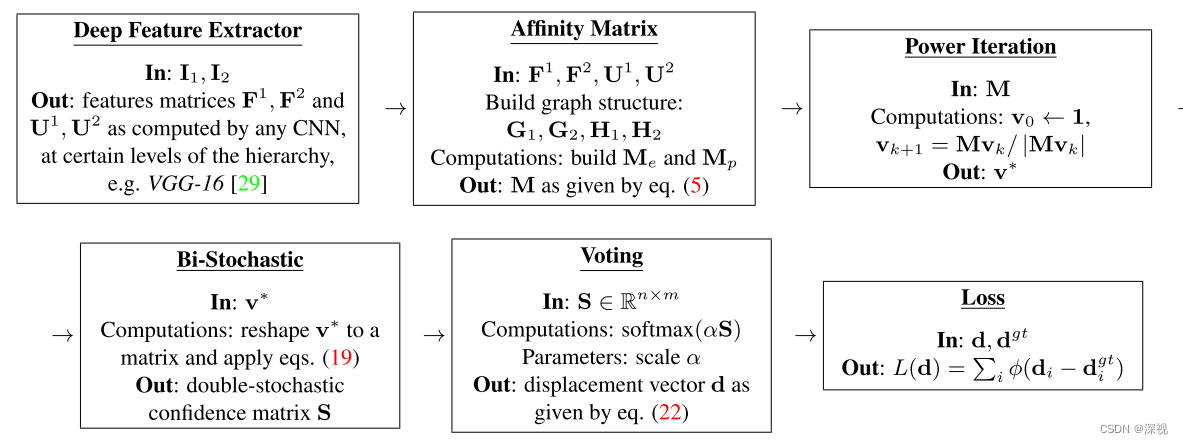
实现过程
首先,输入两幅图像 I 1 , I 2 I_1,I_2 I1,I2,使用CNN,如VGG-16,分别对图像进行特征提取,其中relu5-1层输出的特征向量 F F F作为边特征, r e l u 4 2 relu4_2 relu42层输出的特征向量 U U U作为节点特征。如果图像带有标记好的关键点则直接采用关键点进行构图,否则通过均匀采样的方式进行关键点提取。得到两幅图对应的关键点集后,对于图像 I 1 I_1 I1采用Delaunay三角剖分的方式构建图 G 1 \mathcal{G}_1 G1,图像 I 2 I_2 I2采用全连接方式构建图 G 2 \mathcal{G}_2 G2。
完成图构建后,可以得到邻接矩阵 A 1 , A 2 A_1,A_2 A1,A2,为方便后续采用因式分解图匹配的形式,将邻接矩阵转化成节点-边指示矩阵(node-edge incidence matrix)的形式 G 1 , G 2 , H 1 , H 2 G_1,G_2,H_1,H_2 G1,G2,H1,H2,关于这种描述形式的介绍可以参看这篇博客。然后计算关联矩阵 M M M
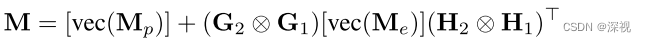
其中 M p M_p Mp和 M e M_e Me分别表示节点关联矩阵和边关联矩阵,计算方法如下
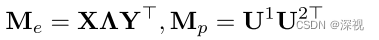
其中 Λ \Lambda Λ表示可学习参数, X , Y X,Y X,Y分别表示两幅图对应的节点特征,计算方式如下
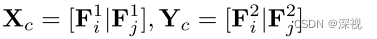
得到关联矩阵 M M M后,需要计算两幅图之间的最优的匹配关系。本文采用幂迭代的方式计算得到 M M M的主特征向量 v ∗ v^* v∗
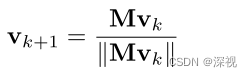
初始 v 0 = 1 v_0=\mathbf{1} v0=1为数值全为1的向量, ∥ ∥ \|\| ∥∥表示 l 2 l_2 l2范数。经过 N N N次迭代得到 v ∗ = v N v^*=v_N v∗=vN.
得到特征向量 v ∗ v^* v∗后,将其变形为 n × m n\times m n×m大小的矩阵, n , m n,m n,m分别表示两幅图的节点数量。再通过重复进行行列归一化处理,得到双随机矩阵 S S S
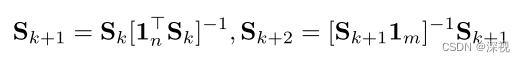
初始 S 0 = ( v ∗ ) n × m S_0=(v^*)_{n\times m} S0=(v∗)n×m。双随机矩阵 S S S可以看作是匹配置信度得分图,数值越大对应的两个点匹配的概率越高。为了方便计算损失,作者将置信度得分图 S S S转化成一个偏移向量,描述预测的匹配点坐标和原节点坐标之间的位置偏移。
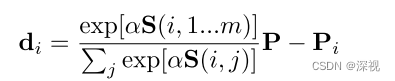
α \alpha α是一个权重参数, S ( i , 1... m ) S(i,1...m) S(i,1...m)表示 S S S的第 i i i行,包含 m m m个数值分别描述了图 G 2 \mathcal{G}_2 G2中 m m m个节点与图 G 1 \mathcal{G}_1 G1中第 i i i个节点之间的匹配概率, P P P表示 m m m个节点对应的坐标。这里可以理解为将 m m m个节点的位置进行加权求和,权重就是经过规范化处理的匹配置信度得分。
最后,损失函数计算方法如下
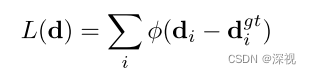
其中 ϕ ( x ) = x T x + ϵ \phi(x)=\sqrt{x^Tx+\epsilon} ϕ(x)=xTx+ϵ是一个鲁棒地惩罚项, d g t d^{gt} dgt表示原点和匹配点之间真实的偏移量。原文中还给出了每一步计算的反向传播梯度计算方法,过程比较复杂这里就不展开介绍了,感兴趣的可以去查看原文。创新点
- 首次提出一种基于深度学习的图匹配网络
- 提出各个阶段计算的新范式和对应的反向传播方法
算法评价
本文是图匹配领域划时代的作品了,后续大部分基于深度学习的图匹配方法都是按照该文的范式进行改进的,包括边特征和节点特征的提取方式,关联矩阵的计算,双随机矩阵计算等等。文章还给出了每一个步骤反向传播,梯度计算的具体推导过程,理论基础也是十分扎实的。
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。
-
相关阅读:
【Redis高手修炼之路】Jedis——Jedis的基本使用
DTSE Tech Talk | 第11期:深入浅出畅谈华为云低时延直播技术
理解RNN以及模型搭建代码
非对称加密BTC算法面试题
[SQL]数据查询(一)
迈向无限可能, ATEN宏正领跑设备切换行业革命!
卡尔曼滤波之基本概念和状态观测器
音频基础模型LTU(Listen, Think, and Understand)
【深度学习实验】前馈神经网络(四):自定义逻辑回归模型:前向传播、反向传播算法
深度学习系列1——Pytorch 图像分类(LeNet)
- 原文地址:https://blog.csdn.net/qq_36104364/article/details/127776487