主成分分析PCA并给出解释百分比

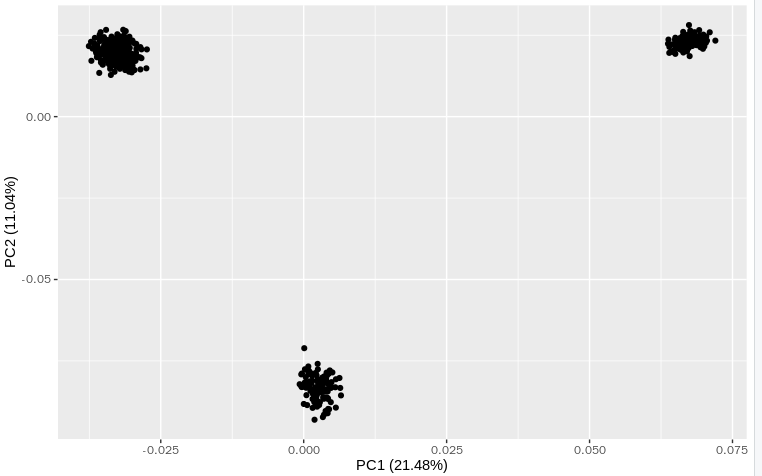
出图：包括PC1和PC2的散点图，以及PC1和PC2的解释百分比。

1. 处理思路

思路：
1，根据plink文件，进行pca分析
2，根据特征值，计算pca1和pca2的解释百分比
3，根据特征向量结果，进行pca作图

2. 注意事项

注意：

特征值就是特征向量在对应维度的方差，特征值所占所有特征值之和的比值，就是其对应特征向量的方差贡献率。

简单来说：

• PCA1是特征向量，其方差是PC1的特征值，其方差贡献率为PC1特征值的百分比
• PCA2是特征向量，其方差是PC2的特征值，其方差贡献率为PC2特征值的百分比

3. 示例演示

示例：
比如计算一个plink进行文件的3个pca，结果如下：

plink --bfile geno/b --pca 3

1
2

结果包括：

• plink.eigenval ，特征值，共有3行数据，分别是3个PCA的特征值
• plink.eigenvec，特征向量，第三四五列是3个PCA的特征向量，作图用前两个PCA

$ head plink.eigenvec
0 ID1 -0.032 0.0185407 0.0351135
0 ID2 -0.0330665 0.0213082 0.0575101
0 ID3 -0.0340043 0.0209365 -0.00264537
0 ID4 -0.0323621 0.0203962 0.0503156
0 ID5 -0.0325016 0.0191183 0.0426273
0 ID6 -0.0346765 0.0196053 -0.0408817

1
2
3
4
5
6
7
8

$ head plink.eigenval
145.367
74.7594
6.10604

1
2
3
4
5

4. 计算PCA百分比

如果想要十分精确的计算每个PCA的得分，那我们需要计算所有PCA的值，PCA的个数等于样本的个数。

比如我们的样本有575个，那么它计算PCA的代码为：

plink --bfile geno/b --pca 575

1
2

可以看到，样本数和pca的行数都是575行

$ wc -l geno/b.fam
575 geno/b.fam
$ wc -l plink.eigenvec
575 plink.eigenvec
$ wc -l plink.eigenval
575 plink.eigenval

1
2
3
4
5
6
7

在R语言中计算每个PCA的百分比，以及PCA可视化：

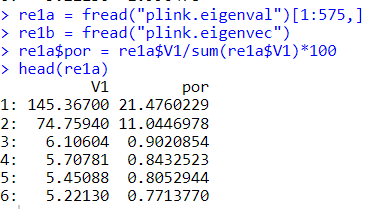
library(tidyverse)
library(tidyverse)
re1a = fread("plink.eigenval")
re1b = fread("plink.eigenvec")

re1a$por = re1a$V1/sum(re1a$V1)*100
head(re1a)

ggplot(re1b,aes(x = V3,y = V4)) + geom_point() + 
  xlab(paste0("PC1 (",round(re1a$por[1],2),"%)")) + 
  ylab(paste0("PC2 (",round(re1a$por[2],2),"%)")) 
1
2
3
4
5
6
7
8
9
10
11

结果：

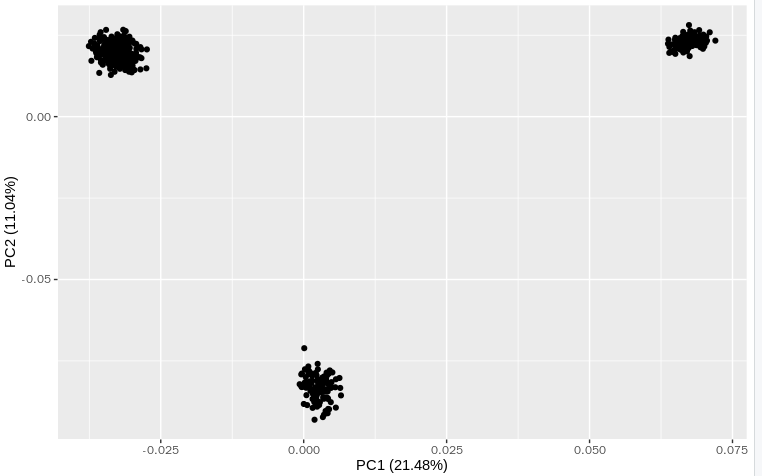
5. 使用前10个做PCA百分比计算

因为PCA的特征向量从大到小排列，所以，也可以用前3个或者前10个作为代表，计算PC1和PC2的百分比，我们测试一下：

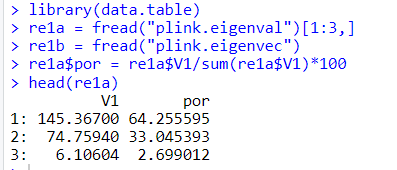
取前三个
这个偏差太大了，PC1从原来的21%，到现在的64%，不靠谱！

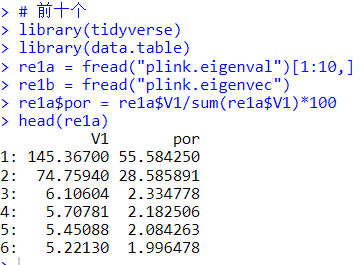
取前十个
也不靠谱，变化也比较大，还是老老实实的用所有的特征值去计算百分比吧，麻雀虽小，积土成山呀！

取所有
这个才是最正确的！

6. 一步到位

现在的问题是，样本的个数，还要查看，然后定义–pca number，再读取，可以在R中一步到位：

思路：

• 读取plink文件的fam，确定个数
• R中调用plink，传参个数
• 作图

args="geno/b"
nn = dim(fread(paste0(args[1],".fam"),header=F))[1]
system(sprintf("~/bin/plink --bfile %s --allow-extra-chr --chr-set 30 --pca %s",args[1],nn))
re1a = fread("plink.eigenval")
re1b = fread("plink.eigenvec")

re1a$por = re1a$V1/sum(re1a$V1)*100
head(re1a)

ggplot(re1b,aes(x = V3,y = V4)) + geom_point() + 
  xlab(paste0("PC1 (",round(re1a$por[1],2),"%)")) + 
  ylab(paste0("PC2 (",round(re1a$por[2],2),"%)")) 
1
2
3
4
5
6
7
8
9
10
11
12
13