-
机器学习笔记之条件随机场(三)MEMM的标注偏置问题
机器学习笔记之条件随机场——MEMM的标注偏置问题
引言
上一节介绍了隐马尔可夫模型(Hidden Markov Model,HMM)向最大熵马尔可夫模型(Maximum Entropy Markov Model,MEMM)的演化过程。本节将针对MEMM模型的缺陷,并介绍 条件随机场(Condition Random Field,CRF)。
回顾:最大熵马尔可夫模型
最大熵马尔可夫模型的 观测状态 O \mathcal O O 可分为全局影响(Global)和局部影响(Local)两种:
- 全局影响意味着 将所有观测变量
o
1
,
⋯
,
o
T
o_1,\cdots,o_T
o1,⋯,oT视为一个结点。对应概率图描述如下:
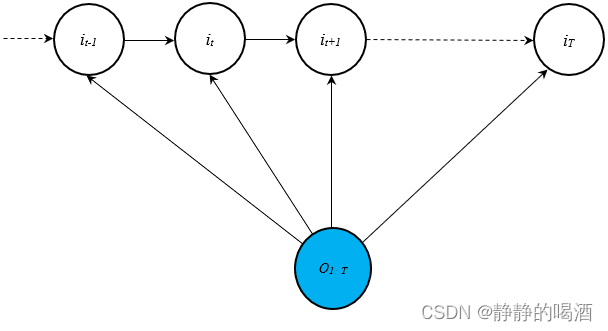
对应建模对象 P ( I ∣ O ; λ ) \mathcal P(\mathcal I \mid \mathcal O;\lambda) P(I∣O;λ)表示如下:
P ( I ∣ O ; λ ) = P ( i 1 ∣ O ; λ ) ⋅ ∏ t = 2 T P ( i t ∣ i t − 1 , O ; λ ) \mathcal P(\mathcal I \mid \mathcal O;\lambda) = \mathcal P(i_1 \mid \mathcal O;\lambda) \cdot \prod_{t=2}^T \mathcal P(i_t \mid i_{t-1},\mathcal O ;\lambda) P(I∣O;λ)=P(i1∣O;λ)⋅t=2∏TP(it∣it−1,O;λ) - 局部影响意味着 各时刻的观测变量
o
t
o_t
ot与对应时刻的隐变量
i
t
i_t
it进行关联,但各时刻的观测变量独立性被打破。对应概率图描述如下:
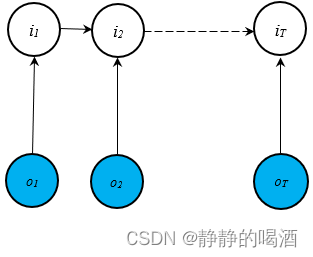
对应建模对象 P ( I ∣ O ; λ ) \mathcal P(\mathcal I \mid \mathcal O;\lambda) P(I∣O;λ)表示如下:
P ( I ∣ O ; λ ) = P ( i 1 , ⋯ , i T ∣ o 1 , ⋯ , o T ; λ ) = P ( i 1 ∣ o 1 ; λ ) ⋅ ∏ t = 2 T P ( i t ∣ i t − 1 , o t ; λ ) P(I∣O;λ)=P(i1,⋯,iT∣o1,⋯,oT;λ)=P(i1∣o1;λ)⋅T∏t=2P(it∣it−1,ot;λ) P(I∣O;λ)=P(i1,⋯,iT∣o1,⋯,oT;λ)=P(i1∣o1;λ)⋅t=2∏TP(it∣it−1,ot;λ)
最大熵马尔可夫模型的优点
和隐马尔可夫模型相比,最大熵马尔可夫模型的优点体现在两个方面:
- 最大熵马尔可夫模型是 概率判别模型,在解码任务(Decoding)中,相比于隐马尔可夫模型,使用更少的计算量对最优隐状态序列进行求解:
I ^ = arg max I P ( I ∣ O ; λ ) = arg max i 1 P ( i 1 ∣ O ; λ ) ⋅ ∏ t = 2 T arg max i t P ( i t ∣ i t − 1 , O ; λ ) ˆI=argmaxIP(I∣O;λ)=argmaxi1P(i1∣O;λ)⋅T∏t=2argmaxitP(it∣it−1,O;λ) I^=IargmaxP(I∣O;λ)=i1argmaxP(i1∣O;λ)⋅t=2∏TitargmaxP(it∣it−1,O;λ)
相比之下,马尔可夫模型使用维特比算法(Viterbi)使用联合概率分布的迭代方式求解最优状态序列:
δ t ( k ) = max i 1 , ⋯ , i t − 1 P ( o 1 , ⋯ , o t , i 1 , ⋯ , i t − 1 , i t = q k ; λ ) δ t + 1 ( j ) = max i 1 , ⋯ , i t P ( o 1 , ⋯ , o t + 1 , i 1 , ⋯ , i t , i t + 1 = q j ; λ ) δ t + 1 ( j ) = δ t ( k ) ⋅ a k j ⋅ b j ( o t + 1 ) δt(k)=maxi1,⋯,it−1P(o1,⋯,ot,i1,⋯,it−1,it=qk;λ)δt+1(j)=maxi1,⋯,itP(o1,⋯,ot+1,i1,⋯,it,it+1=qj;λ)δt+1(j)=δt(k)⋅akj⋅bj(ot+1) δt(k)δt+1(j)δt+1(j)=i1,⋯,it−1maxP(o1,⋯,ot,i1,⋯,it−1,it=qk;λ)=i1,⋯,itmaxP(o1,⋯,ot+1,i1,⋯,it,it+1=qj;λ)=δt(k)⋅akj⋅bj(ot+1)
但是,含隐变量联合概率分布的计算代价要明显高于条件概率的计算。 - 最大熵马尔可夫模型打破了观测独立性假设,它使得观测变量间存在关联关系,相比观测独立性假设在序列标注任务(解码任务)中更加合理。
最大熵马尔可夫模型的缺陷
MEMM的缺陷是:造成标注偏置问题(Label Bias Problem)的出现。
标注偏置问题
如果使用一句话描述该问题:在状态转移的过程中,条件概率分布的熵值越低,那么状态转移过程越忽视观测变量。
本来是通过观测变量的差异性 来描述隐变量的条件概率结果;但如果熵值过低,导致观测变量的差异性几乎没有对条件概率结果产生影响,最终使状态转移结果与给定观测结果不匹配。
标注偏置问题示例
假设存在如下词语数据集:
D = { ′ r o b ′ , ′ r o b ′ , ′ r o b ′ , ′ r i b ′ } \mathcal D = \{'rob','rob','rob','rib'\} D={′rob′,′rob′,′rob′,′rib′}- 正常情况下,学习过程中 概率图结构表示如下:
这个MEMM概率图结构并不严谨,详细见下面红字。
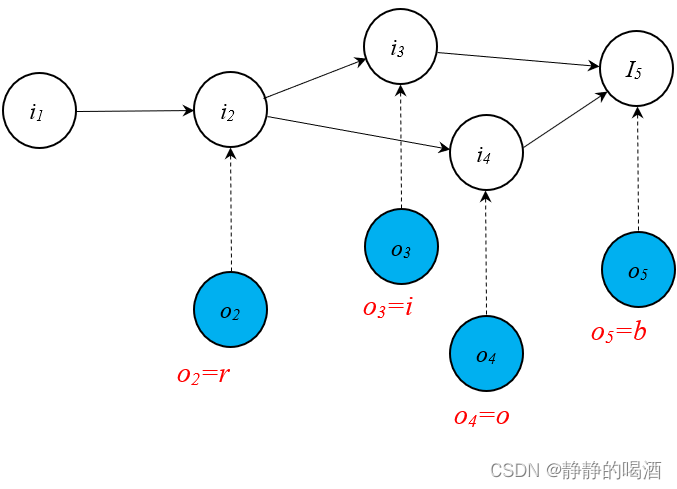
在学习过程(Learning)中,从初始状态 i 1 i_1 i1经过第一次观测进行状态转移,最终得到状态 i 2 i_2 i2。状态 i 2 i_2 i2的条件概率结果表示如下:
由于四个单词的‘首字母’均相同,均为r r r。因此,无论是哪个样本,第一次观测的结果均是同一结果。
P ( i 2 ∣ i 1 , o 2 = r ) = 4 4 = 1 \mathcal P(i_2 \mid i_1,o_2=r) = \frac{4}{4} =1 P(i2∣i1,o2=r)=44=1
以此类推,在状态 i 2 i_2 i2的条件下,经过第二次观测,状态转移至 i 3 , i 4 i_3,i_4 i3,i4的条件概率结果分别表示如下:
四个样本在第二次观测中,o o o占了三个,i i i占了一个,根据概率的频率定义,其状态转移的条件概率取决于当前时刻观测变量出现的频率。
P ( i 3 ∣ i 2 , o 3 = i ) = 1 4 P ( i 4 ∣ i 2 , o 4 = o ) = 3 4 P(i3∣i2,o3=i)=14P(i4∣i2,o4=o)=34 P(i3∣i2,o3=i)=41P(i4∣i2,o4=o)=43
最终的第三次观测,所有样本点的观测结果均是 b b b。因此有:
P ( i 5 ∣ i 3 , o 5 = b ) = P ( i 5 ∣ i 4 , o 5 = b ) = 1 \mathcal P(i_5 \mid i_3,o_5=b) = \mathcal P(i_5 \mid i_4,o_5=b) = 1 P(i5∣i3,o5=b)=P(i5∣i4,o5=b)=1
上述状态转移过程中,条件概率结果与观测变量的差异性之间存在密切关系。在解码任务(Decoding)中,假设给定 观测序列: r i b rib rib,对应的 P ( I ∣ O ; λ ) \mathcal P(\mathcal I \mid \mathcal O;\lambda) P(I∣O;λ)表示如下:
真正的开始是从i 2 i_2 i2,而i 3 , i 4 i_3,i_4 i3,i4并不是两个独立的隐变量,而是同一个隐变量在不同概率下的转移结果。这里为了表述方便,将其分成两个部分。但在公式表达中需要将其合并。
P ( i 4 ∣ i 2 , o 4 = i ) = 0 \mathcal P(i_4 \mid i_2,o_4 = i) = 0 P(i4∣i2,o4=i)=0恒成立。因为o 4 o_4 o4选择不了i i i。
I ^ = arg max I P ( I ∣ O = r i b ; λ ) = arg max I P ( i 2 , i 3 , i 4 , i 5 ∣ O = r i b ) = arg max i 2 P ( i 2 ∣ i 1 , o 2 = r ) ⋅ arg max i 3 , i 4 [ P ( i 3 ∣ i 2 , o 3 = i ) , P ( i 4 ∣ i 2 , o 4 = i ) ] ⋅ arg max i 5 [ P ( i 5 ∣ i 3 , o 5 = b ) , P ( i 5 ∣ i 4 , o 5 = b ) ] = P ( i 2 ∣ i 1 , o 2 ) ⋅ P ( i 3 ∣ i 2 , o 3 ) ⋅ P ( i 5 ∣ i 3 , o 5 ) ˆI=argmaxIP(I∣O=rib;λ)=argmaxIP(i2,i3,i4,i5∣O=rib)=argmaxi2P(i2∣i1,o2=r)⋅argmaxi3,i4[P(i3∣i2,o3=i),P(i4∣i2,o4=i)]⋅argmaxi5[P(i5∣i3,o5=b),P(i5∣i4,o5=b)]=P(i2∣i1,o2)⋅P(i3∣i2,o3)⋅P(i5∣i3,o5) I^=IargmaxP(I∣O=rib;λ)=IargmaxP(i2,i3,i4,i5∣O=rib)=i2argmaxP(i2∣i1,o2=r)⋅i3,i4argmax[P(i3∣i2,o3=i),P(i4∣i2,o4=i)]⋅i5argmax[P(i5∣i3,o5=b),P(i5∣i4,o5=b)]=P(i2∣i1,o2)⋅P(i3∣i2,o3)⋅P(i5∣i3,o5)
至此,找到最优路径 I ^ = { i 1 , i 2 , i 3 , i 5 } \hat {\mathcal I} = \{i_1,i_2,i_3,i_5\} I^={i1,i2,i3,i5} - 基于相同的数据集合,学习过程将概率图结构修改成如下形式:
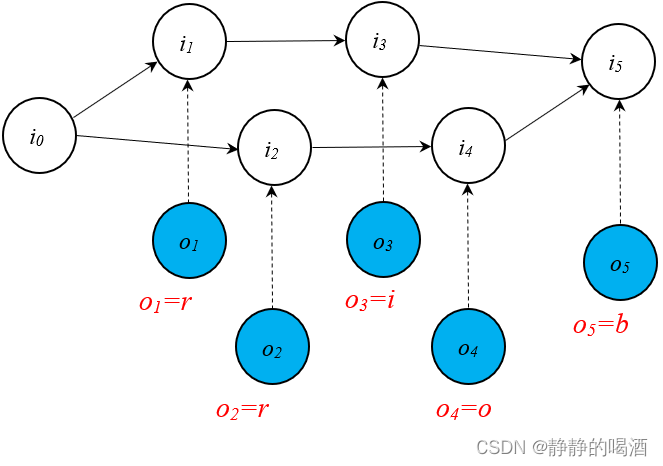
该图和上图正常情况之间的区别在于:该图是从路径的角度进行划分,而上图是从时刻的角度进行划分。
在学习过程中,初始状态 i 0 i_0 i0在第一次观测后进行状态转移,分别转移至 i 1 , i 2 i_1,i_2 i1,i2的条件概率表示如下:
不同于正常情况,此时i 0 i_0 i0存在两条路径,虽然观测结果全部是r r r,但从路径的角度观察,存在3 4 \frac{3}{4} 43概率是样本r o b rob rob中的r r r,而仅有1 4 \frac{1}{4} 41概率是样本r i b rib rib中的r r r。
P ( i 2 ∣ i 0 , o 2 = r ) = 3 4 P ( i 1 ∣ i 0 , o 1 = r ) = 1 4 P(i2∣i0,o2=r)=34P(i1∣i0,o1=r)=14 P(i2∣i0,o2=r)=43P(i1∣i0,o1=r)=41
核心步骤:无论是 i 1 i_1 i1还是 i 2 i_2 i2,它均只存在唯一一条路径, i 1 → i 3 , i 2 → i 4 i_1 \to i_3,i_2 \to i_4 i1→i3,i2→i4,没有其他选择。这样会导致在该时刻的观测变量无论是什么,都不影响其唯一路径的选择。也就是说,此时的观测变量并不对状态转移过程产生影响:
在路径被确定的条件下,i 1 i_1 i1的概率分布(出度)只有一种选择。
P ( i 3 ∣ i 1 , o 3 = i ) = P ( i 3 ∣ i 1 ) = 1 P ( i 4 ∣ i 2 , o 4 = o ) = P ( i 4 ∣ i 2 ) = 1 \mathcal P(i_3 \mid i_1,o_3 = i) = \mathcal P(i_3 \mid i_1) = 1 \\ \mathcal P(i_4 \mid i_2,o_4 = o) = \mathcal P(i_4 \mid i_2) = 1 P(i3∣i1,o3=i)=P(i3∣i1)=1P(i4∣i2,o4=o)=P(i4∣i2)=1
同理,后续结点由于路径的确定同样也被确定,对应结果如下:
相比于上一步骤的影响差了很多,因为无论哪条路径,其最后的观测结果都是b b b
P ( i 5 ∣ i 3 , o 5 = b ) = P ( i 5 ∣ i 3 ) = 1 P ( i 5 ∣ i 4 , o 5 = b ) = P ( i 5 ∣ i 4 ) = 1 \mathcal P(i_5 \mid i_3,o_5 = b) = \mathcal P(i_5 \mid i_3) = 1 \\ \mathcal P(i_5 \mid i_4,o_5 = b) = \mathcal P(i_5 \mid i_4) = 1 P(i5∣i3,o5=b)=P(i5∣i3)=1P(i5∣i4,o5=b)=P(i5∣i4)=1
如果此时给定观测序列: r i b rib rib,再次观察最优路径:
I ^ = arg max I P ( I ∣ O = r i b ; λ ) = arg max I [ P ( i 2 ∣ i 0 , o 2 = r ) ⋅ P ( i 4 ∣ i 2 , o 4 = o ) ⋅ P ( i 5 ∣ i 4 , o 5 = b ) ] , [ P ( i 1 ∣ i 0 , o 1 = r ) ⋅ P ( i 3 ∣ i 1 , o 3 = i ) ⋅ P ( i 5 ∣ i 3 , o 5 = b ) ] = P ( i 2 ∣ i 0 , o 2 = r ) ⋅ P ( i 4 ∣ i 2 , o 4 = o ) ⋅ P ( i 5 ∣ i 4 , o 5 = b ) ˆI=argmaxIP(I∣O=rib;λ)=argmaxI[P(i2∣i0,o2=r)⋅P(i4∣i2,o4=o)⋅P(i5∣i4,o5=b)],[P(i1∣i0,o1=r)⋅P(i3∣i1,o3=i)⋅P(i5∣i3,o5=b)]=P(i2∣i0,o2=r)⋅P(i4∣i2,o4=o)⋅P(i5∣i4,o5=b) I^=IargmaxP(I∣O=rib;λ)=Iargmax[P(i2∣i0,o2=r)⋅P(i4∣i2,o4=o)⋅P(i5∣i4,o5=b)],[P(i1∣i0,o1=r)⋅P(i3∣i1,o3=i)⋅P(i5∣i3,o5=b)]=P(i2∣i0,o2=r)⋅P(i4∣i2,o4=o)⋅P(i5∣i4,o5=b)
最优路径 I ^ = { i 0 , i 2 , i 4 , i 5 } \hat {\mathcal I}= \{i_0,i_2,i_4,i_5\} I^={i0,i2,i4,i5},但这个最优路径描述的观测序列是 r o b rob rob,与给定序列不符合。
从熵的角度观察观测变量存在差异性的部分:
- 正常情况下:
3 4 log 4 3 + 1 4 log 4 ≈ 0.5623 \frac{3}{4}\log \frac{4}{3} + \frac{1}{4} \log 4 \approx 0.5623 43log34+41log4≈0.5623 - 标注偏置现象:
0 log 0 + 1 log 1 = 0.0 0 \log 0 + 1 \log 1 = 0.0 0log0+1log1=0.0
标注偏置现象使得观测变量存在差异的部分熵更小,在最大熵思想一节中熵值小意味着概率分布相差较大,距离“等可能”的效果越远,此时状态转移过程概率分布可能已经内定给概率结果大的隐状态,而当前时刻的观测值作用很小,甚至没有作用。
下一节将介绍条件随机场。
- 全局影响意味着 将所有观测变量
o
1
,
⋯
,
o
T
o_1,\cdots,o_T
o1,⋯,oT视为一个结点。对应概率图描述如下:
-
相关阅读:
5进程创建FORK
为什么选择快速应用开发
【NLP】预训练模型——GPT1
使用kube-bench检测Kubernetes集群安全
可添加头尾的RecycleView的实现
嵌入式分享合集87
力扣84 双周赛 t4 6144 和力扣305周赛t4 6138
Win10怎么重启资源管理器?重启资源管理器快捷键是什么
LeetCode 40. Combination Sum II【回溯,剪枝】中等
纳科星融资逾2亿美元用于电池材料生产
- 原文地址:https://blog.csdn.net/qq_34758157/article/details/127765816