JZ69 跳台阶 JZ71 跳台阶扩展问题 JZ10 斐波那契数列

JZ69 跳台阶

描述
一只癞蛤蟆一次可以跳上1级台阶，也可以跳上2级。求该癞蛤蟆跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

分析问题：
1级台阶：一种跳法：1
2级台阶：二种跳法：1+1、2
3级台阶：三种跳法：1+1+1、1+2、2+1
4级台阶：五种跳法：1+1+1+1、1+1+2、1+2+1、2+1+1、2+2

发现规律：当前项跳法等于前两项之和

解法一：递归：

public int jumpFloor(int target) {
   if(target<=2){
       return target;
   }
   return jumpFloor(target-1)+jumpFloor(target-2);
}
1
2
3
4
5
6

解法二：动态规划：

public int jumpFloor(int target) {
    int[] arr = new int[target+1];
    for(int i=1;i<=target;i++){
        if(i<=2){
            arr[i]=i;
        }else{
            arr[i]=arr[i-1]+arr[i-2];
        }
    } 
    return arr[target];
}
1
2
3
4
5
6
7
8
9
10
11

动态规划优化：因为只使用到了前两项的值，因此可以借助中间变量来存储前两项的值

public int jumpFloor(int target) {
   int a=1,b=1,c=1;
   for(int i=2;i<=target;i++){
       c=a+b;
       a=b;
       b=c;
   }
   return c;
}
1
2
3
4
5
6
7
8
9

总结：

JZ71 跳台阶扩展问题

描述
一只癞蛤蟆一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该癞蛤蟆跳上一个n级的台阶(n为正整数)总共有多少种跳法。

分析问题：
1级台阶：一种跳法：1
2级台阶：二种跳法：1+1、2
3级台阶：三种跳法：1+1+1、1+2、2+1、3
4级台阶：五种跳法：1+1+1+1、1+1+2、1+2+1、2+1+1、2+2、3+1、1+3、4

发现规律：当前项n的跳法等于前一项的2倍，也就是2[^n-1]

解法一：递归：

public int jumpFloorII(int target) {
   if(target<=1){
       return 1;
   }else{
       return jumpFloorII(target-1)*2;
   }
}
1
2
3
4
5
6
7

解法二：动态规划：

public int jumpFloorII(int target) {  
  int[] arr = new int[target+1];
  arr[1]=1;
  for(int i=2;i<=target;i++){
      arr[i] = arr[i-1]*2;
  }
  return arr[target];
}
1
2
3
4
5
6
7
8

动态规划优化

public int jumpFloorII(int target) {
  int a=1;
  int b=1;
  for(int i=2;i<=target;i++){
      a=b*2;
      b=a;
  }
   return a;
}
1
2
3
4
5
6
7
8
9

解法三：快速幂：

直接优化为求2的n-1次幂

public int jumpFloorII(int target) {
    int a=1;
    for(int i=2;i<=target;i++){
        a*=2;
    }
    return a;
}
1
2
3
4
5
6
7

优化为求解2的快速幂

public int jumpFloorII(int target) {
   if(target==1){
       return 1;
   }
   return fast(target-1);
}

public int fast(int target) {
    if(target==1){
       return 2;
   }
   int temp = fast(target/2);
   if(target%2==0){
       return temp*temp;
   }else{
       return temp*temp*2;
   }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

JZ10 斐波那契数列

解法一：递归：

public int Fibonacci(int n) {
     if(n<=2){
         return 1;
     }else{
         return Fibonacci(n-1)+Fibonacci(n-2);
     }
 }
1
2
3
4
5
6
7

解法二：动态规划：

public int Fibonacci(int n) {
   int[] arr = new int[n+1];
   for(int i=1;i<=n;i++){
       if(i<=2){
           arr[i]=1;
       }else{
           arr[i]=arr[i-1]+arr[i-2];
       }
   }
   return arr[n];
}
1
2
3
4
5
6
7
8
9
10
11

动态规划优化

public int Fibonacci(int n) {
 if(n<=2){
     return 1;
 }
 int a=1,b=1,c=1;
 for(int i=3;i<=n;i++){
     c=a+b;
     a=b;
     b=c;
 }
 return c;
}
1
2
3
4
5
6
7
8
9
10
11
12

JZ70 矩形覆盖

描述
我们可以用 21 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 21 的小矩形无重叠地覆盖一个 2*n 的大矩形，从同一个方向看总共有多少种不同的方法？
注意：约定 n == 0 时，输出 0

分析图解：难点在于找规律，找出所有的情况，不能漏掉。第一次分析时漏掉了2*4的最后一种情形，看题解才发现。当不确定的时候，可以试试N再加一，看看规律是否依旧成立来验证。
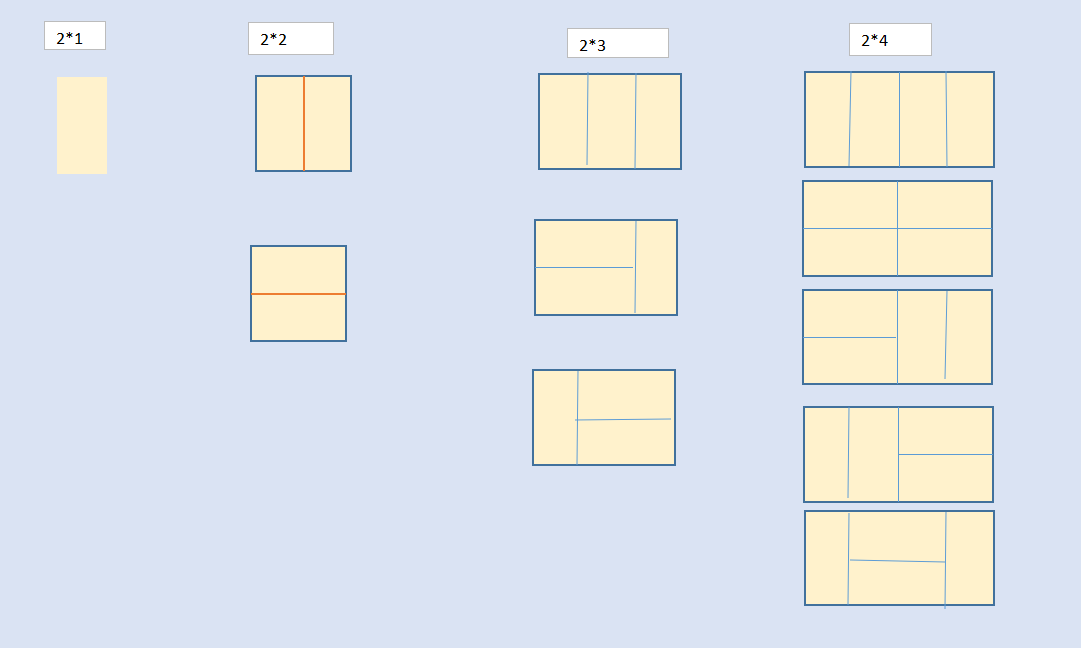解法一：递归：

public int rectCover(int target) {
    if(target<=2){
        return target;
    }
    return rectCover(target-1)+rectCover(target-2);
}
1
2
3
4
5
6

解法二：动态规划：

public int rectCover(int target) {
int[] dp = new int[target + 1];
for (int i = 0; i <= target; i++) {
    if (i <= 2) {
        dp[i] = i;
    } else {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
}
return dp[target];
}
1
2
3
4
5
6
7
8
9
10
11

动态规划优化：

public int rectCover(int target) {
  if(target<2){
      return target;
  }
  int a=1,b=1,c=1;
  for(int i=2;i<=target;i++){
      c=a+b;
      a=b;
      b=c;
  }
  return c;
}
1
2
3
4
5
6
7
8
9
10
11
12

总结：此四题都是非常简单的动态规划的入门题。
涉及数据结构：数组
涉及算法：递归、动态规划、快速幂