• pytorch深度学习实战lesson9

    第九课 线性回归

    理论部分

    线性回归

    案例：美国房价预测

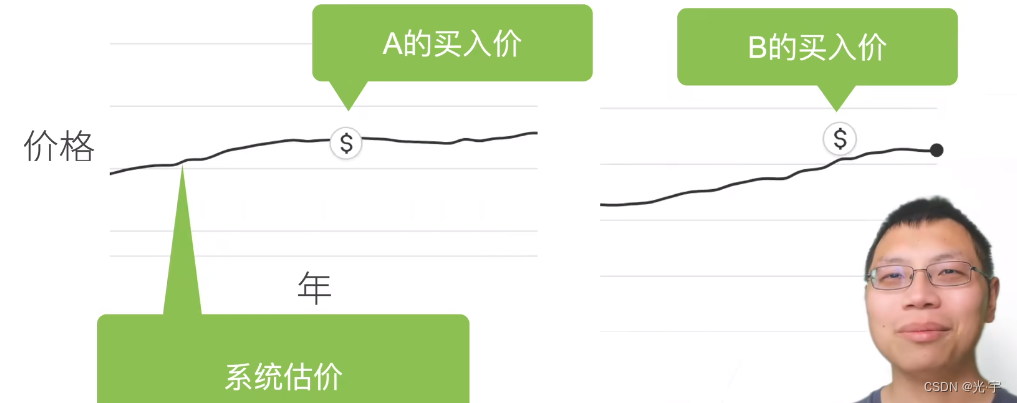
    系统估价和自己实际付的钱要保持差不多的关系才能使自己赚到，那怎么样才能赚到呢，那就得有一个量良好的预估手段。

    下面做出两个假设：

    线性模型可以看做是单层的神经网络

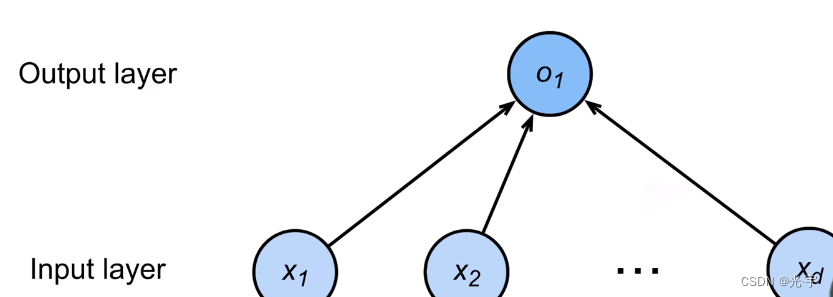
    每个箭头代表一个权重，输出是o1，输入是xn

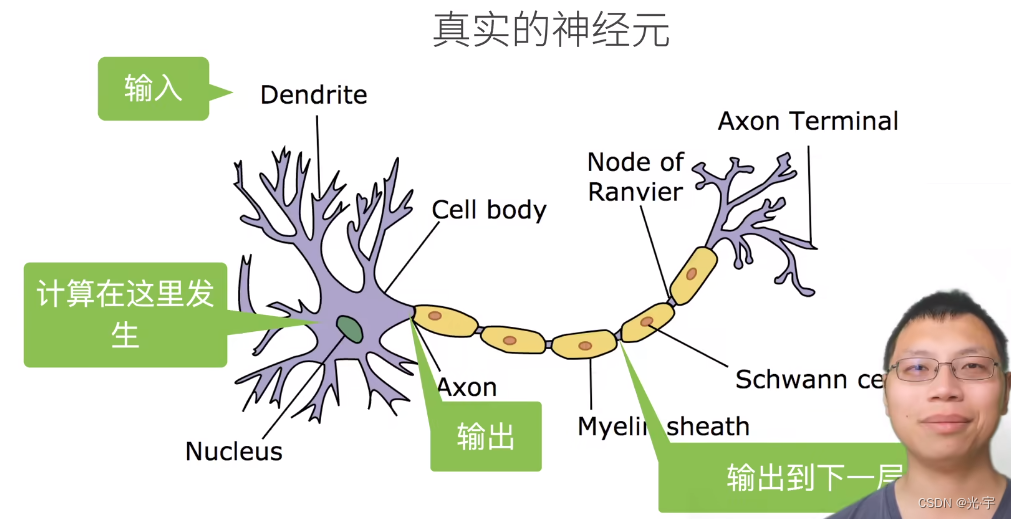
    神经网络其实源于神经科学，下图是真实的神经元：

    有了模型之后，就要对其进行预测了，放在上面的案例里面讲也就是比较房价的真实值和预估值。

    这个相当于是神经网络里面的损失函数。

    有了模型和损失后，下一步就是参数的学习。

    可以收集一些数据点来决定参数值（权重和偏差），比如过去六个月卖的房子，这些数据就被称为是训练数据，通常来讲，训练数据越多越好。

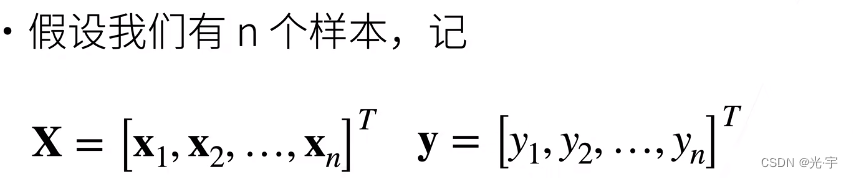
    X是列向量，每个x一排一排的排好然后做转置。然后y是列向量有n个样本，每个y是实数样本。

    目标是找到一个w和b使得损失函数的结果最小。

    总结

    1、线性回归是对n维输入的加权，外加偏差。

    2、使用平方损失来衡量预测值和真实值的差异。

    3、线性回归有显示解。

    4、线性回归可以看做是单层神经网络。

    基础优化方法

    优化方法最常用的是梯度下降算法。

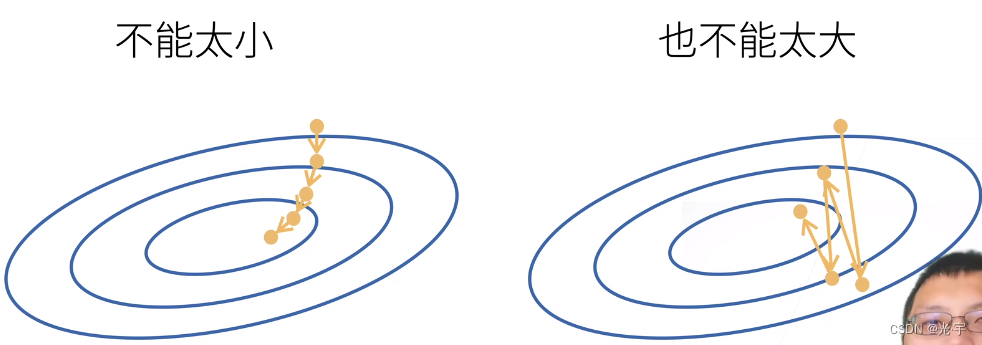
    这里的学习率不能太大也不能太小，因为太小的话耗费资源很多，太大的话就错过最优值了。

    总结：

    1、梯度下降通过不断沿着反梯度方向更新参数求解

    2、小批量随机梯度下降是深度学习默认的求解算法

    3、两个重要的超参数是批量大小和学习率

    实践部分

    线性回归从零开始实现：

    1. #￥￥￥￥￥<<<<<+++++-----线性回归从零开始实现-----+++++>>>>>￥￥￥￥￥#
    2. #从零开始实现整个方法，包括流水线、模型、损失函数和小批量随机梯度下降优化器
    3. #%matplotlib_inline                                 #用于随机梯度下降和初始化权重
    4. import matplotlib.pyplot as plt
    5. import torch
    6. import random
    7. from d2l import torch as d2l
    8. #根据带有噪声的线性模型构造一个人造数据集，我们使用线性模型参数w=[2,-3,4]T、b=4.2和噪声e生成数据集及其标签：
    9. #y=Xw+b+e
    10. def synthetic_data(w,b,num_examples):               #构造人造数据集，num_examples是要生成的样本数量
    11.     '''生成 y=Xw+b+e'''
    12.     X=torch.normal(0,1,(num_examples,len(w)))       #构造x是方差为零均值为1的随机数，它的大小是样本数，它的列数是w的长度
    13.     y=torch.matmul(X,w)+b                           #构造y
    14.     y+=torch.normal(0,0.01,y.shape)                 #又让y加上了一个噪音。噪音是方差为0，均值为0.01,形状与y一样
    15.     return X,y.reshape((-1,1))                      #把x和y做出列向量返回
    16.  
    17. true_w=torch.tensor([2,-3.4])                       #定义真实的w和真实的b
    18. true_b=4.2
    19. features,labels=synthetic_data(true_w,true_b,1000)  #然后通过函数计算出特征和标注
    20.  
    21. #看一下训练样本的样子以及样本分布图
    22. print('features:',features[0],'\nlable:',labels[0]) #输出：features: tensor([0.4727, 0.1651]) lable: tensor([4.5845])
    23.                                                     #可见，第零个样本是长为2的一个向量，其标号是标量
    24. print('########################################################')
    25. d2l.set_figsize()
    26. d2l.plt.scatter(features[:,(1)].detach().numpy(),labels.detach().numpy(),1)#detach的作用是在pytorch的一些版本中，
    27.                                                                             # 需要从计算图中detach处来才能转到numpy中
    28. plt.show()                                          #画完后我们可以看到是个线性相关的样本集
    29. #定义一个data_iter 函数， 该函数接收批量大小、
    30. def data_iter(batch_size, features, labels):
    31.                                                     # 特征矩阵和标签向量作为输入，生成大小为batch_size的小批量
    32.     num_examples = len(features)
    33.     indices = list(range(num_examples))             #生成每个样本的索引（每个样本是随机读取的，没有特定顺序）
    34.     random.shuffle(indices)                         #打乱下标
    35.     for i in range(0, num_examples, batch_size):    #从0开始到num_examples,每次走batch_size个
    36.         batch_indices = torch.tensor(
    37. indices[i:min(i +batch_size, num_examples)])        #这里要获取批量索引，把索引存入张量中，后面的min操作是防止超过总量，所以要取最小的
    38.         yield (features[batch_indices],             #通过indices生成特征和标号。yield相当于是Python中的重复操作，
    39.                labels[batch_indices])               #每次都生成一个x一个y，生成完后再调用函数，直到全部完成为止。
    40.  
    41. batch_size = 10
    42.  
    43. for X, y in data_iter(batch_size, features, labels):#给我一些样本标号，每次随机选取b个样本返回出来
    44.     print(X, '\n', y)
    45.     break
    46. print('########################################################')
    47. #定义初始化模型参数
    48. w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)#w是2*1的，2表示特征，1表示标签，0表示方差，0.02表示均值
    49. b = torch.zeros(1, requires_grad=True)              #b初始赋为零，1表示它是1维的标量
    50.                                                     #w和b的requires_grad都是true表示它们要计算梯度，实时更新
    51. #定义模型
    52. def linreg(X, w, b):                                #-----线性回归模型
    53.     return torch.matmul(X, w) + b
    54. #定义损失函数
    55. def squared_loss(y_hat, y):                         #-----均方损失
    56.     return (y_hat - y.reshape(y_hat.shape))**2 / 2  #y_hat是预测值，y是真实值，要保证两者形状统一，差先按元素平方然后按元素除二
    57. #定义优化算法
    58. def sgd(params, lr, batch_size):                    #-----小批量随机梯度下降，params是个列表，里面包含w和b
    59.     with torch.no_grad():                           #它不需要计算梯度
    60.         for param in params:                        #每一个w和b
    61.             param -= lr * param.grad / batch_size   #param=param-lr*param.grad/batch_size除以batch_size的操作是求均值操作，
    62.                                                     #由于是线性关系，所以在此求均值也可。
    63.             param.grad.zero_()                      #梯度置零
    64. #开始训练
    65. #先定义超参数
    66. lr = 0.03                                           #学习率
    67. num_epochs = 3                                      #把整个数据扫三遍，也就是进行三轮训练
    68. net = linreg                                        #模型就是之前定义的linreg
    69. loss = squared_loss                                 #损失还是之前的定义的
    70. for epoch in range(num_epochs):                     #每一次对数据扫一遍
    71.     for X, y in data_iter(batch_size, features, labels):#每次拿出一组x和y
    72.         l = loss(net(X, w, b), y)                   #把预测的y和真实的y做损失，出来的损失是长为批量大小的向量
    73.         l.sum().backward()                          #求和之后算梯度
    74.         sgd([w, b], lr, batch_size)                 #更新参数
    75.     with torch.no_grad():
    76.         train_l = loss(net(features, w, b), labels) #计算损失，不用算梯度
    77.         print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
    78. print('########################################################')
    79. #比较真实参数和通过训练学到的参数来评估训练的成功程度
    80. print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
    81. print(f'b的估计误差: {true_b - b}')
    82.  
    83. #可以实验一下梯度很大或梯度很小时的情况，看看其损失有什么变化
    84. #梯度很大时
    85. '''#先定义超参数
    86. lr = 10                                           #学习率
    87. num_epochs = 10                                      #把整个数据扫三遍，也就是进行三轮训练
    88. net = linreg                                        #模型就是之前定义的linreg
    89. loss = squared_loss                                 #损失还是之前的定义的
    90. for epoch in range(num_epochs):                     #每一次对数据扫一遍
    91.     for X, y in data_iter(batch_size, features, labels):#每次拿出一组x和y
    92.         l = loss(net(X, w, b), y)                   #把预测的y和真实的y做损失，出来的损失是长为批量大小的向量
    93.         l.sum().backward()                          #求和之后算梯度
    94.         sgd([w, b], lr, batch_size)                 #更新参数
    95.     with torch.no_grad():
    96.         train_l = loss(net(features, w, b), labels) #计算损失，不用算梯度
    97.         print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')'''
    98. #梯度很小时，可以通过增加学习轮次得到好一些的损失值，但是成本有点大
    99. '''#梯度很大时
    100. #先定义超参数
    101. lr = 0.001                                           #学习率
    102. num_epochs = 3                                      #把整个数据扫三遍，也就是进行三轮训练
    103. net = linreg                                        #模型就是之前定义的linreg
    104. loss = squared_loss                                 #损失还是之前的定义的
    105. for epoch in range(num_epochs):                     #每一次对数据扫一遍
    106.     for X, y in data_iter(batch_size, features, labels):#每次拿出一组x和y
    107.         l = loss(net(X, w, b), y)                   #把预测的y和真实的y做损失，出来的损失是长为批量大小的向量
    108.         l.sum().backward()                          #求和之后算梯度
    109.         sgd([w, b], lr, batch_size)                 #更新参数
    110.     with torch.no_grad():
    111.         train_l = loss(net(features, w, b), labels) #计算损失，不用算梯度
    112.         print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')'''

    features: tensor([ 0.3840, -0.3376]) 
    lable: tensor([6.1121])
    ########################################################
    tensor([[-1.1147e+00, -8.3294e-01],
            [-6.0542e-04,  2.1474e-02],
            [ 9.3246e-01,  1.4499e+00],
            [ 4.7537e-01, -2.9177e-01],
            [ 1.8271e+00,  1.3387e-01],
            [-3.8728e-01, -1.7065e+00],
            [-2.3963e+00, -1.5596e-01],
            [-1.7679e+00, -6.3735e-01],
            [ 4.8884e-01,  1.1035e+00],
            [-6.9350e-01,  2.9550e-01]]) 
     tensor([[ 4.7953],
            [ 4.1320],
            [ 1.1461],
            [ 6.1476],
            [ 7.3970],
            [ 9.2280],
            [-0.0416],
            [ 2.8342],
            [ 1.4362],
            [ 1.8041]])
    ########################################################
    epoch 1, loss 0.026386
    epoch 2, loss 0.000093
    epoch 3, loss 0.000046
    ########################################################
    w的估计误差: tensor([0.0001, 0.0004], grad_fn=)
    b的估计误差: tensor([0.0007], grad_fn=)

    线性回归简洁实现：

    1. #所谓的简洁实现就是通过使用深度学习框架来简洁地实现 线性回归模型 生成数据集
    2. import numpy as np
    3. import torch
    4. from torch.utils import data                                #处理数据的模块
    5. from d2l import torch as d2l
    6.  
    7. true_w = torch.tensor([2, -3.4])                            #真实的w
    8. true_b = 4.2                                                #真实的b
    9. features, labels = d2l.synthetic_data(true_w, true_b, 1000) #生成特征和标签
    10. #调用框架中现有的API来读取数据
    11. def load_array(data_arrays, batch_size, is_train=True):
    12.     """构造一个PyTorch数据迭代器。"""
    13.     dataset = data.TensorDataset(*data_arrays)              #先将x,y变成dataset数据集
    14.     return data.DataLoader(dataset, batch_size,             #然后调用dataloader，每次挑b个样本出来
    15.                            shuffle=is_train)                #如果在训练过程中的话就要随机打乱顺序
    16.  
    17. batch_size = 10
    18. data_iter = load_array((features, labels), batch_size)
    19.  
    20. next(iter(data_iter))                                       #得到一个x和一个y
    21. #使用框架的预定义好的层
    22. from torch import nn
    23. net = nn.Sequential(nn.Linear(2, 1))                        #要指定输入输出维度，linear是个线性层，
    24.                                                             # 把他放在sequential里的话就相当于把每层给罗列起来了
    25. #初始化模型参数
    26. net[0].weight.data.normal_(0, 0.01)                         #把权重初始化
    27. net[0].bias.data.fill_(0)                                   #把偏重初始化
    28. #计算均方误差使用的是MSELoss类，也称为平方 L2 范数
    29. loss = nn.MSELoss()                                         #均方误差的调用
    30. #实例化 SGD 实例
    31. trainer = torch.optim.SGD(net.parameters(), lr=0.03)        #梯度下降的调用，要传入所有参数（w，b）,和学习参数
    32. #训练过程代码与我们从零开始实现时所做的非常相似
    33. num_epochs = 3
    34. for epoch in range(num_epochs):
    35.     for X, y in data_iter:
    36.         l = loss(net(X), y)          #net自己带模型参数了
    37.         trainer.zero_grad()          #先梯度清零
    38.         l.backward()                 #pytorch已经做sum了
    39.         trainer.step()               #模型更新
    40.     l = loss(net(features), labels)
    41.     print(f'epoch {epoch + 1}, loss {l:f}')
    42. #比较生成数据集的真实参数和通过有限数据训练获得的模型参数
    43. w = net[0].weight.data
    44. print('w的估计误差：', true_w - w.reshape(true_w.shape))
    45. b = net[0].bias.data
    46. print('b的估计误差：', true_b - b)

    epoch 1, loss 0.000369
    epoch 2, loss 0.000104
    epoch 3, loss 0.000105
    w的估计误差： tensor([-0.0004, -0.0009])
    b的估计误差： tensor([-5.7220e-06])

  • 相关阅读:
    通用接口平台开源版正式发布2.0版本
    Linux Day16 多线程的一些常见问题
    Python正则表达式
    SpringBoot Kafka生产者 多kafka配置
    从云AK泄露利用看企业特权管理
    js正则表达式
    计算机毕业论文选题推荐|软件工程|系列十一
    提高采购效率，采购管理的五大原则及实现方法
    Qt6.3学习笔记 QFrame::HLine与QFrame::VLine 改变线条颜色
    Postman抓包网页请求
  • 原文地址：https://blog.csdn.net/weixin_48304306/article/details/127773206