LeetCode_动态规划_中等_764.最大加号标志

1.题目

在一个 n x n 的矩阵 grid 中，除了在数组 mines 中给出的元素为 0，其他每个元素都为 1。mines[i] = [x_i, y_i]表示 grid[x_i][y_i] == 0

返回 grid 中包含 1 的最大的轴对齐加号标志的阶数。如果未找到加号标志，则返回 0 。

一个 k 阶由 1 组成的 “轴对称”加号标志具有中心网格 grid[r][c] == 1 ，以及4个从中心向上、向下、向左、向右延伸，长度为 k-1，由 1 组成的臂。注意，只有加号标志的所有网格要求为 1 ，别的网格可能为 0 也可能为 1 。

示例 1：

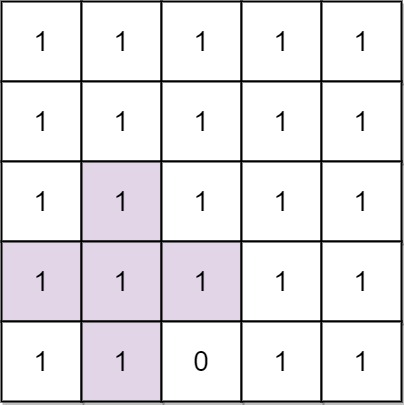
输入: n = 5, mines = [[4, 2]]
输出: 2
解释: 在上面的网格中，最大加号标志的阶只能是2。一个标志已在图中标出。

示例 2：

输入: n = 1, mines = [[0, 0]]
输出: 0
解释: 没有加号标志，返回 0 。

提示：
1 <= n <= 500
1 <= mines.length <= 5000
0 <= xi, yi < n
每一对 (x_i, y_i) 都 不重复

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/largest-plus-sign

2.思路

（1）暴力穷举法
① 构建矩阵 n * n 的矩阵 grid，此处为了简化构建的过程，将原本的 0 和 1 进行互换；

② 使用变量 res 记录最大加号阶数，其初始值为 0；

③ 遍历 grid 中的每一个网格，如果当前网格中的值为 0：
1）使用变量 minDis 记录当前网格 grid[i][j] 到四个方向边界的最小距离，即加号阶数的上限；
2）剪枝操作：如果 minDis 小于等于 res，那么无需判断中心网格为 grid[i][j] 的加号标志，直接跳过即可；
3）否则，计算从当前网格遍历的四个方向的最大距离，分别记录为 up、down、left、right；
4）最短的一个方向的距离决定了加号的阶数，此时再更新 res 即可。

④ 遍历结束后，直接返回 res。

（2）动态规划
思路参考该 LeetCode 用户题解。

3.代码实现（Java）

//思路1————暴力穷举法
class Solution {
    public int orderOfLargestPlusSign(int n, int[][] mines) {
        //为了简化构建矩阵 grid，此处将原本的 0 和 1 进行互换
        int[][] grid = new int[n][n];
        for (int[] mine : mines) {
            grid[mine[0]][mine[1]] = 1;
        }
        // res 记录最大加号阶数
        int res = 0;
        //遍历 grid 中的每一个网格
        for (int i = 0; i < n ;i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 0) {
                    // minDis 记录当前网格到四个方向边界的最小距离，即加号阶数的上限
                    int minDis = Math.min(Math.min(i + 1, j + 1), Math.min(n - i, n - j));
                    //剪枝操作：如果 minDis 小于等于 res，那么无需判断中心网格为 grid[i][j] 的加号标志
                    if (minDis <= res) {
                        continue;
                    }
                    //定义从当前网格遍历的四个方向的最大距离
                    int up = 0;
                    int down = 0;
                    int left = 0;
                    int right = 0;
                    while (i - up >= 0 && grid[i - up][j] == 0) {
                        up++;
                    }
                    while (i + down < n && grid[i + down][j] == 0) {
                        down++;
                    }
                    while (j - left >= 0 && grid[i][j - left] == 0) {
                        left++;
                    }
                    while (j + right < n && grid[i][j + right] == 0) {
                        right++;
                    }
                    //最短的一个方向的距离决定加号的阶数
                    minDis = Math.min(Math.min(up, down), Math.min(left, right));
                    //更新 res
                    res = Math.max(res, minDis);
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

//思路2————动态规划
class Solution {
    public int orderOfLargestPlusSign(int n, int[][] mines) {
        // dp[i][j] 表示以 grid[i][j] 为中心的最大加号标志的阶数
        int[][] dp = new int[n][n];
        //初始化 dp
        for (int[] line : dp) {
            Arrays.fill(line, n);
        }
        for (int[] mine : mines) {
            dp[mine[0]][mine[1]] = 0;
        }
        for (int i = 0; i < n; i++) {
            int up = 0;
            int down = 0;
            int left = 0;
            int right = 0;
            for (int j = 0, k = n - 1; j < n; j++, k--) {
                up = dp[j][i] > 0 ? up + 1 : 0;
                down = dp[k][i] > 0 ? down + 1 : 0;
                left = dp[i][j] > 0 ? left + 1 : 0;
                right = dp[i][k] > 0 ? right + 1 : 0;
                dp[j][i] = Math.min(dp[j][i], up);
                dp[k][i] = Math.min(dp[k][i], down);
                dp[i][j] = Math.min(dp[i][j], left);
                dp[i][k] = Math.min(dp[i][k], right);
            }
        }
        //答案为所有 dp[i][j] 的最大值
        int res = 0;
        for (int[] line : dp) {
            res = Math.max(res, Arrays.stream(line).max().getAsInt());
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36