[杂记]算法: 快慢指针

---

打算以后记录一些比较有代表性的算法. 仅从初学者角度对算法进行简单解读, 以力扣题为例.

---

0. 快慢指针

快慢指针是双指针的一种. 一般来说, 在判断存不存在环结构的时候比较有用. 通常来讲, 我们通过指针进行遍历, 快指针一次走两步, 慢指针一次走一步, 快慢指针相遇往往就意味着某些我们想要的信息. 还是以例题为素材.

1. 环形链表

题目链接: 环形链表II

题目要求我们找到链表入环的第一个节点. 如果判断链表是否存在环, 则只需要让快指针一次走两步, 慢指针一次走一步, 判断二者是否相遇即可. 但是要找到第一个节点, 我们需要先写出公式进行推导.

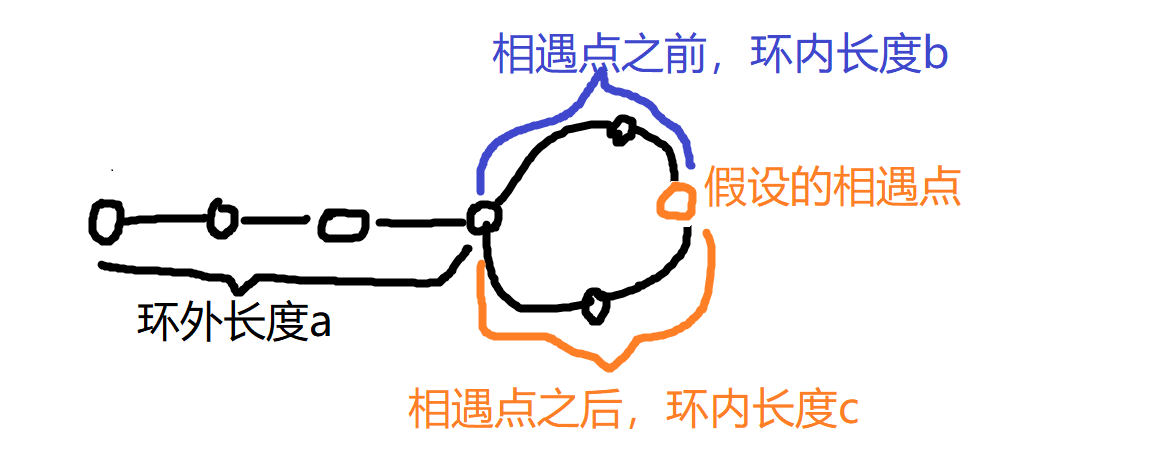
如图, 我们假设环外的直线部分的长度为$a$(在这里为3), 在相遇点之前环中的长度为$b$, 相遇点之后环中的长度为$c$, 当然$b+c=环长$.

假设在相遇的时候, 快指针已经在环内走了$n,n\ge 1$圈, 那么慢指针走过的长度一定是$a+b$. 快指针走的长度是$a+b+n(b+c)$

慢指针走过的长度不可能是$a+kb,k\ge 2$, 因为如果慢指针走过完整的环, 则其必与快指针相遇. 这是因为考虑二者的相对速度, 在慢指针看来, 快指针的速度为1个单位, 所以快指针必在一个环内追上慢指针.

我们利用快指针走过的长度一定是慢指针的2倍这个事实, 得到
$$a+b+n(b+c)=2(a+b)$$

我们要求的是进入环的第一个节点, 也就是a的值, 化简上式得到:

$$a=c+(n-1)(b+c)$$

因此, a一定是环长的倍数加c, 这意味着, 如果我们将慢指针从相遇点再往下遍历, 同时找一个辅助指针auxPtr从头开始, 则慢指针与auxPtr相遇的时候, 慢指针绕过了$n-1$圈再多$c$, 而auxPtr走到$a$, 正是环的入口处.

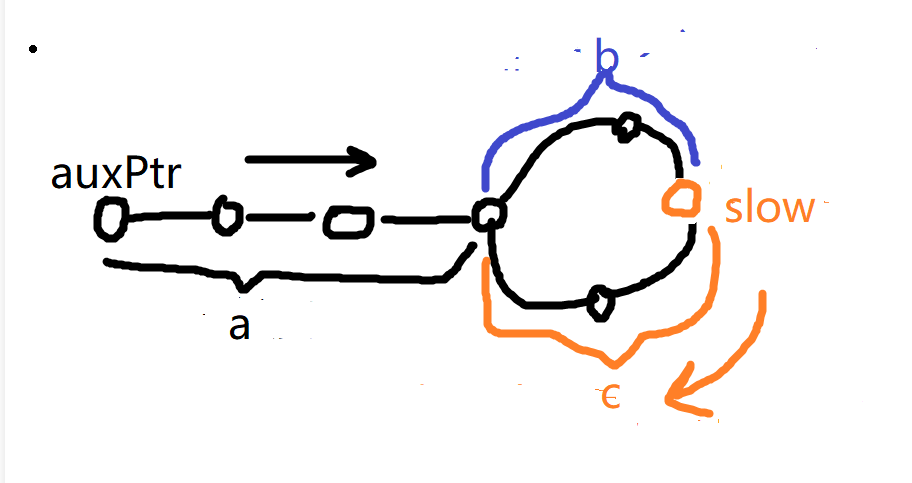
当fast可能到达链表末尾时, 说明不存在环, 返回null. 因此编写程序如下:

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head, *slow = head;  // 定义快慢指针
        ListNode* auxPtr = head;  // 辅助指针

        while(fast) {
            slow = slow->next;
            if (fast->next) fast = fast->next->next; 
            else break;

            if (fast == slow) {  // 若相遇 表明有环 辅助指针与慢指针同时走
                while (auxPtr != slow) {
                    auxPtr = auxPtr->next;
                    slow = slow->next;
                }
                return auxPtr;
            }
        }

        return nullptr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

2. 寻找重复的数

题目链接: 寻找重复数

有一个长度为$n+1$的数组, 每个元素的范围都在$[1,n]$内, 根据鸽巢原理, 必存在一个重复的数. 找到这个重复的数.

这道题也是可以通过快慢指针法求解的. 我们还是将数组想象成一个链表, 然而并不是按照数组顺序排列的链表. 假设一个数组, 其索引2和4的位置的值都为3, 如下所示:

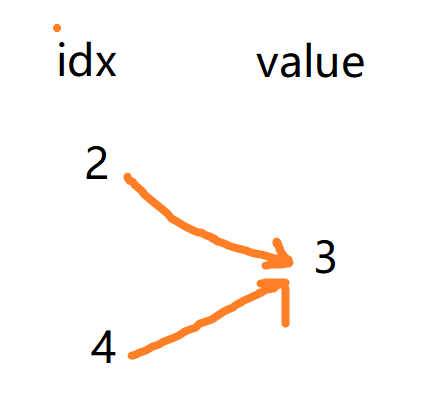
那么我们考虑$idx\to nums[idx]$的映射, 当$idx=2$时, 我们得到$3$, 我们再考虑$nums[3]$, 它的值可以是随便一个数, 但是一定不会超过数组的长度$n$. 因此如此下去, 这个$nums[idx]$的值必然会回到2或4(因为假设数组中没有4, 则还可以再回到2), 因此, 回到2或4之后再次进行映射, 就又回到了重复值3. 因此上题中$\to next$的操作在本题中相当于进行$nums[idx]$的映射, 从3再回到3的过程, 就是在环中遍历的过程, 这个过程当然可长可短.

因此编写代码如下:

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int slow = 0, fast = 0;

        do {
            slow = nums[slow]; // slow = slow->next
            fast = nums[nums[fast]];  // fast = fast->next->next
        } while(slow != fast);

        int auxPtr = 0;
        while(slow != auxPtr) {
            auxPtr = nums[auxPtr];
            slow = nums[slow];
        }
        return auxPtr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18