-
leetcode刷题（129）——576. 出界的路径数
给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你 最多 可以移动 maxMove 次球。
给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 109 + 7 取余 后的结果。
示例 1：
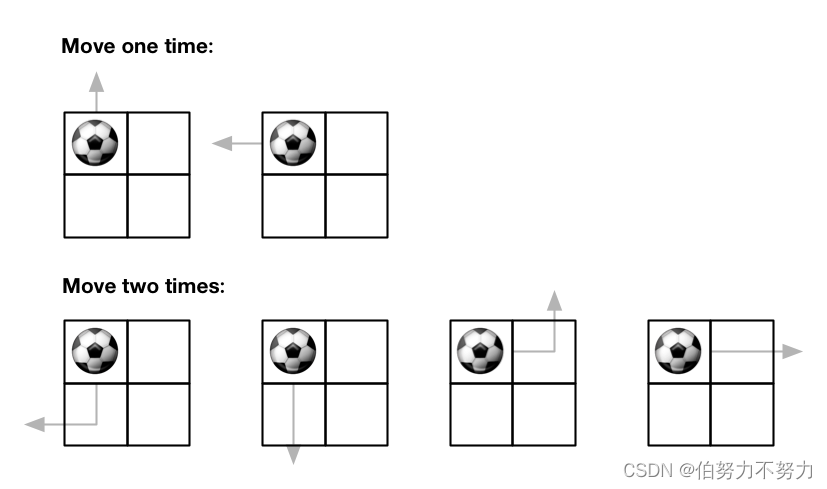
输入：m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0 输出：6- 1
- 2
示例 2：
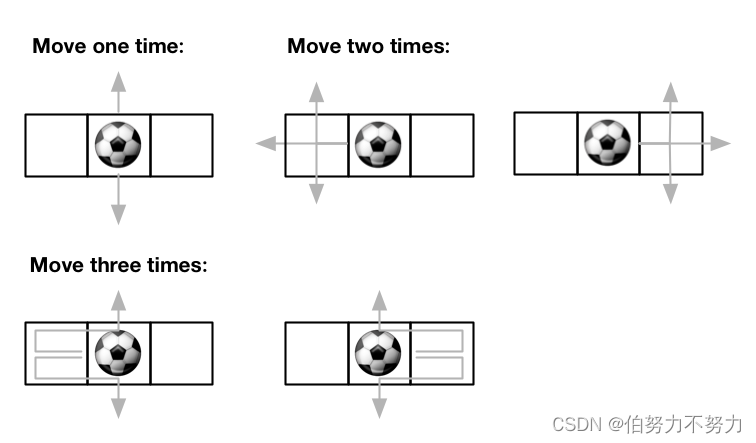
输入：m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1 输出：12- 1
- 2
提示：
1 <= m, n <= 50
0 <= maxMove <= 50
0 <= startRow < m
0 <= startColumn < n方法一、DFS
刚看到这题，感觉还挺简单的，这不就是一个简单的 DFS 嘛，从给定的起点，一直往下深搜，直到 i 和 j 超出边界了就说明找到了一条路径，如果在给定的移动次数范围内还没有越界，那这条路径就不符合要求。
OK，代码比较简单，请看注释：
class Solution { // 四个方向 int[][] dirs = new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 取余 int MOD = 1000000007; public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) { return dfs(m, n, maxMove, startRow, startColumn); } private int dfs(int m, int n, int moveCount, int i, int j) { // 越界了就找到了一条路径 if (i < 0 || j < 0 || i >= m || j >= n) { return 1; } // 没有移动次数了，返回0 if (moveCount == 0) { return 0; } // 从这个点出发的符合条件的路径数量 int sum = 0; for (int[] dir : dirs) { // 记得取余 sum = (sum + dfs(m, n, moveCount - 1, i + dir[0], j + dir[1])) % MOD; } return sum; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
超时：
方法二、DFS + 剪枝
既然普通的DFS无法满足条件，肯定是需要加上一些剪枝的技巧的，那我们来看看哪些地方可以剪枝呢？
试想，给定如下网络，小球在中间的位置，给定的移动次数为2，可以看到这时候小球不管怎么移动，都不会超出网格。
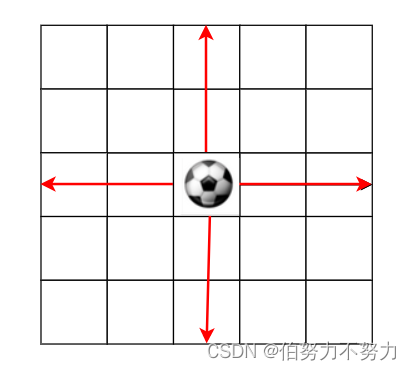
所以，剪枝技巧就是每次DFS的时候判断如果小球不管怎么移动都无法超出网格，那从这个点开始往后的枝就都可以剪掉了，简单修改下代码即可：class Solution { // 四个方向 int[][] dirs = new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 取余 int MOD = 1000000007; public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) { return dfs(m, n, maxMove, startRow, startColumn); } private int dfs(int m, int n, int moveCount, int i, int j) { // 越界了就找到了一条路径 if (i < 0 || j < 0 || i >= m || j >= n) { return 1; } // 没有移动次数了，返回0 if (moveCount == 0) { return 0; } // 剪枝：如果小球不管怎么移动都无法越出网格，那就剪掉这个枝 if (i - moveCount >= 0 && j - moveCount >= 0 && i + moveCount < m && j + moveCount < n) { return 0; } // 从这个点出发的符合条件的路径数量 int sum = 0; for (int[] dir : dirs) { // 记得取余 sum = (sum + dfs(m, n, moveCount - 1, i + dir[0], j + dir[1])) % MOD; } return sum; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
依然超时：
方法三、记忆化搜索
剪枝也不行，我们再深入思考一下。
请看下图，假设我们的起始位置是在 A 位置，最多可以移动 6 步，我们可以很容易地发现，会有很多次经过B位置的情况，而从 B 位置出去我们只需要计算一次就可以了，比如，图中列举了三种到达 B 位置的情况。
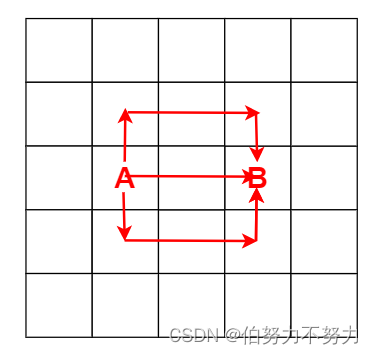
所以，第三种方法，我们需要增加一个缓存，记录下来从每个位置在给定移动次数的范围内可以越界的次数，这就是记忆化搜索。请看代码，我们增加了一个三维数组作为缓存，前两维表示位置，第三维表示移动次数：
class Solution { // 四个方向 int[][] dirs = new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 取余 int MOD = 1000000007; public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) { // 缓存 int[][][] memo = new int[m][n][maxMove + 1]; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { for (int k = 0; k <= maxMove; k++) { memo[i][j][k] = -1; } } } return dfs(m, n, maxMove, startRow, startColumn, memo); } private int dfs(int m, int n, int moveCount, int i, int j, int[][][] memo) { // 越界了就找到了一条路径 if (i < 0 || j < 0 || i >= m || j >= n) { return 1; } // 没有移动次数了，返回0 if (moveCount == 0) { return 0; } // 缓存中存在 if (memo[i][j][moveCount] != -1) { return memo[i][j][moveCount]; } // 剪枝：如果小球不管怎么移动都无法越出网格，那就剪掉这个枝 if (i - moveCount >= 0 && j - moveCount >= 0 && i + moveCount < m && j + moveCount < n) { return 0; } // 从这个点出发的符合条件的路径数量 int sum = 0; for (int[] dir : dirs) { // 记得取余 sum = (sum + dfs(m, n, moveCount - 1, i + dir[0], j + dir[1], memo)) % MOD; } // 记录缓存 memo[i][j][moveCount] = sum; return sum; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
时间复杂度：O(m * n * maxMove)，构建memo及每个位置向下搜索的过程中都是O(m * n * maxMove)的时间复杂度。
空间复杂度：O(m * n * maxMove)，memo数组需要额外占用O(m * n * maxMove)的空间。运行结果：通过
方法四、动态规划
一般来说，能使用记忆化搜索的题目都可以使用动态规划来解。
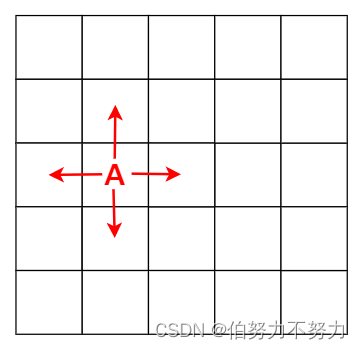
从图中可以看出，A位置的结果是来自于它的上下左右四个方向的结果，所以，我们这样来定义动态规划：dp[i][j][k]表示从 [i,j] 位置最多移动 k 次能够把小球移出去的最大路径数量；
dp[i][j][k] = dp[i-1][j][k-1] + dp[i+1][j][k-1] + dp[i][j-1][k-1] + dp[i][j+1][k-1]；
注意边界条件，如果是正方形的四个顶点，有两种方法越界，其他边上的位置只有一种方法越界。
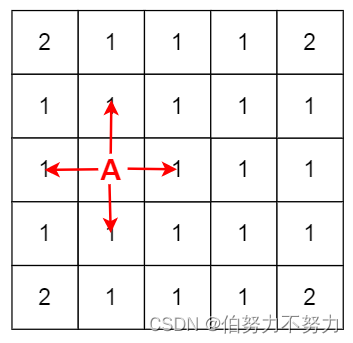
另外，要注意移动次数2的都是从移动次数为1的扩展来的，同理，移动次数3的都是从移动次数为2的扩展来的，所以要注意循环的顺序。代码如下：
class Solution { // 四个方向 int[][] dirs = new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 取余 int MOD = 1000000007; public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) { int[][][] dp = new int[m][n][maxMove + 1]; // 移动步数2的都是从移动步数1的转移来的 // 移动步数3的都是从移动步数2的转移来的 // 所以，要从移动步数从1开始递增 for (int k = 1; k <= maxMove; k++) { for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { // 处理四条边 if (i == 0) dp[i][j][k]++; if (j == 0) dp[i][j][k]++; if (i == m - 1) dp[i][j][k]++; if (j == n - 1) dp[i][j][k]++; // 中间的位置，向四个方向延伸 for (int[] dir : dirs) { int nextI = i + dir[0]; int nextJ = j + dir[1]; if (nextI >= 0 && nextI < m && nextJ >= 0 && nextJ < n) { dp[i][j][k] = (dp[i][j][k] + dp[nextI][nextJ][k - 1]) % MOD; } } } } } return dp[startRow][startColumn][maxMove]; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
时间复杂度：O(m * n * maxMove)，三层循环，dirs的循环固定4次，算常量。
空间复杂度：O(m * n * maxMove)，dp数组占用O(m * n * maxMove)的空间。运行结果：通过
方法五：动态规划 + 终极优化
通过方法四，我们可以看到，计算移动次数为 k 的时候只与 k-1 有关，所以，我们完全没有必要记录 k-1 之前的数据，这里我们可以把移动次数这个维度去掉。
另外，二维数组可以通过一定的方法转换成一维数组。
好了，直接看代码：
class Solution { // 四个方向 int[][] dirs = new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 取余 int MOD = 1000000007; public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) { int[] dp = new int[m * n]; // 移动步数2的都是从移动步数1的转移来的 // 移动步数3的都是从移动步数2的转移来的 // 所以，要从移动步数从1开始递增 for (int k = 1; k <= maxMove; k++) { // 需要声明一个临时数组 // 比如计算[1,2]的时候会用到[2,2]，同时计算[2,2]的时候也会用到[1,2] // 这样计算[1,2]的时候就不能直接把值覆盖了，必须一轮计算完了才能覆盖 int[] tmp = new int[m * n]; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { int index = index(i, j, n); // 处理四条边 if (i == 0) tmp[index]++; if (j == 0) tmp[index]++; if (i == m - 1) tmp[index]++; if (j == n - 1) tmp[index]++; // 中间的位置，向四个方向延伸 for (int[] dir : dirs) { int nextI = i + dir[0]; int nextJ = j + dir[1]; int nextIndex = index(nextI, nextJ, n); if (nextI >= 0 && nextI < m && nextJ >= 0 && nextJ < n) { tmp[index] = (tmp[index] + dp[nextIndex]) % MOD; } } } } dp = tmp; } return dp[index(startRow, startColumn, n)]; } private int index(int i, int j, int n) { return i * n + j; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
时间复杂度：O(m * n * maxMove)，三层循环，dirs的循环固定4次，算常量。
空间复杂度：O(m * n)，dp数组虽然降成了一维，但是仍然要占用O(m * n)的空间运行结果：通过
可以看到，时间基本没变，空间确实降下来了。
但是，仍然没办法跟记忆化搜索相比，因为记忆化搜索我们可以通过剪枝等手段减少循环（递归）的次数，但是动态规划的方法每一轮都要把(m * n)个格子重新计算一遍。
-
相关阅读:
Windows 10注册表损坏该如何修复？
SpringBoot集成Mybatis-Plus
MySQL库表占用空间排序
2 用TensorFlow构建一个简单的神经网络
Java之HashMap经典算法-红黑树(插入节点平衡调整，左旋转，右旋转)
前端实现打印功能Print.js
【数据结构】初始化静态分配的顺序表
2023年煤气证模拟考试题库及煤气理论考试试题
FinalShell或者XShell工具 突然连不上服务器（绝对好使！）
使用 Verilog 做一个可编程数字延迟定时器 LS7211-7212
- 原文地址：https://blog.csdn.net/u012124438/article/details/127758262
